Проверка локальных вариаций

Доступно с лицензией Geostatistical Analyst.

Карты Вороного построены из серии полигонов, сформированных вокруг местоположения выборочной точки.

Полигоны Вороного созданы так, что каждое местоположение в пределах полигона находится ближе к выборочной точке этого полигона, чем любая другая выборочная точка. После создания полигонов, соседи выборочной точки определяются также, как и любая другая выборочная точка, чей полигон граничит с выбранной выборочной точкой. Например, на следующем рисунке яркая зеленая выборочная точка окружена полигоном, который выделен красным цветом. Каждое местоположение в пределах красного полигона находится ближе к яркой зеленой выборочной точке, чем к любой другой выборочной точке (обозначенные маленькими темными синими точками). Все синие полигоны граничат с красным полигоном, так что выборочные точки в пределах синих полигонов являются соседями яркой зеленой выборочной точки.

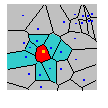
Благодаря определению соседей, можно вычислить множество локальных статистик. Например, среднее значение локальной точки вычисляется как среднее значение выборочных точек в красном и синем полигонах. Среднее значение затем назначается красному полигону. Процесс повторяется для всех полигонов и их соседей, а результаты отображаются с помощью цветового градиента, что позволяет визуализировать участки высоких и низких локальных значений.

Карта Вороного предусматривает следующие методы назначения вычисленных значений полигонам.

• Простое значение (Simple): значение, назначаемое полигону, является значением, зафиксированным в локальной точке в пределах этого полигона.
• Среднее значение (Mean): значение, назначаемое полигону, является средним значением, вычисленным для полигона и его соседей.
• Максимальная плотность распределения (Mode): все полигоны категоризированы с помощью пяти классовых интервалов. Значение, назначаемое полигону, является модой (наиболее часто встречающимся классом) полигона и его соседей.
• Скопление (Cluster): все полигоны категоризированы с помощью пяти классовых интервалов. Если классовый интервал полигона отличается от каждого из его соседа, полигон обозначается серым цветом и помещается в шестой класс, чтобы отличить его от его соседей.
• Энтропия (Entropy): все полигоны категоризированы с помощью пяти классов на основании естественной группировки значений данных (малые квантили). Значение, назначаемое полигону, является энтропией, вычисленной для полигона и его соседей – то есть

  Entropy = - Σ (pi * Log pi ),

  где p_i является пропорциональным делением линии полигонов, назначенных каждому классу. Например, рассмотрим полигон, окружен четырьмя соседями (всего пять полигонов). Значения размещаются в соответствующих классах:

Класс/частота энтропии

Класс	Частота	P i
1	3	3/5
2	0	0
3	1	1/5
4	0	0
5	1	1/5

Энтропия, назначенная полигону, будет

E = -[0.6*log2 (0.6) + 0.2* log2 (0.2) + 0.2* log2 (0.2)] = 1.371

Минимальная энтропия возникает тогда, когда значения полигона расположены в одном и том же классе. Затем,

Emin = -[1 * log2 (1)] = 0

Максимальная энтропия возникает тогда, когда значения каждого полигона расположены в различных классовых интервалах. Затем,

Emax = -[0.2 * log2 (0.2) + 0.2 * log2 (0.2) + 0.2 * log2 (0.2) + 0.2 * log2 (0.2) + 0.2 * log2 (0.2)] = 2.322

• Срединное значение (Median): значение, назначаемое полигону, является срединным значением, вычисленным из плотности распределения полигона и его соседей.
• Стандартное отклонение (Standard Deviation): значение, назначаемое полигону, является стандартным отклонением, вычисленным из полигона и его соседей.
• Межквартильный размах (Interquartile Range): первый и третий квартили вычисляются из плотности распределения полигона и его соседей. Значение, назначаемое полигону, является межквартильным размахом, которое вычислено путем вычитания значения первой квартили из значения третей квартили.

Статистика Вороного может использоваться для различных целей и может быть распределена по следующим функциональным категориям:

Категории общих функций

Функциональная категория	Статистика Вороного
Локальное сглаживание	Среднее значение, максимальная плотность распределения, срединное значение
Локальная вариация	Стандартное отклонение, межквартильный размах, энтропия
Локальные выбросы	Кластер
Локальное влияние	Простое