Доступно с лицензией Geostatistical Analyst.
Вариограмма и функции ковариации дают количественно характеризуют предположение, что объекты, расположенные близко друг к другу, больше похожи между собой, чем удаленные друг от друга на некоторое расстояние. Вариограмма и ковариация измеряют степень статистической корреляции как функцию расстояния.
Процесс моделирования вариограмм и функций ковариации подбирает кривую вариограммы или ковариации к эмпирическим данным. Целью является достижение наилучшего соответствия, а также применение в модели знаний о явлении. Затем модель будет использоваться при интерполяции.
При настройке модели необходимо исследовать направленную автокорреляцию в данных. Важными характеристиками модели являются Диапазон, Порог и Самородок. Если в данных имеются погрешности измерений, используйте модель погрешности измерений. Для получения дополнительных сведений о настройке модели в соответствии с эмпирической вариограммой следуйте по ссылке .
Вариограмма
Вариограмма определяется как
γ(si,sj) = ½ var(Z(si) - Z(sj)),где var является дисперсией.
Если два местоположения, si и sj, близки друг к другу в единицах измерения расстояния d(si, sj), можно ожидать, что они похожи, так что разность их значений, Z(si) – Z(sj), будет мала. По мере дальнейшего удаления i и sj друг от друга они становятся менее похожи, поэтому разность их значений, Z(si) – Z(sj), станет больше. Это можно видеть на следующем рисунке, на котором показано, из чего состоит типичная вариограмма.
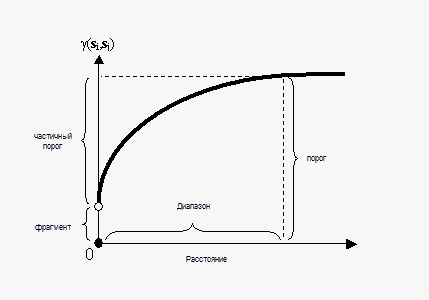
Обратите внимание, что дисперсия разности увеличивается с расстоянием, поэтому вариограмму можно рассматривать как функцию несходства. Имеются несколько терминов, которые часто ассоциируются с этой функцией, и они также используются в ArcGIS Geostatistical Analyst Extension. Высота, которую вариограмма достигает при ее выравнивании, называется порогом. Она часто состоит из двух частей: разрыв в начале координат, называемый эффектом самородка, и частичный порог; вместе они составляют порог. Эффект самородка может быть далее разделен на погрешность измерений и вариацию на микроуровне. Эффект самородка является просто суммой погрешности измерений и вариации на микроуровне, и поскольку какой-нибудь из этих компонентов может быть равен нулю, эффект самородка может целиком состоять из первого или второго компонента. Высота, на которой вариограмма выравнивается до порога, называется диапазоном.
Более подробно о вариограммах, диапазоне, пороге и самородке
Функция ковариации
Функция ковариации определяется как
C(si, sj) = cov(Z(si), Z(sj)),где cov является ковариацией.
Ковариация является масштабируемой версией корреляции. Если два местоположения, si и sj, близки друг к другу, можно ожидать, что они похожи, и их ковариация (корреляция) будет большой. По мере дальнейшего удаления si и sj друг от друга они становятся менее похожи, и их ковариация стремится к нулю. Это можно видеть на следующем рисунке, на котором показано, из чего состоит типичная функция ковариации.
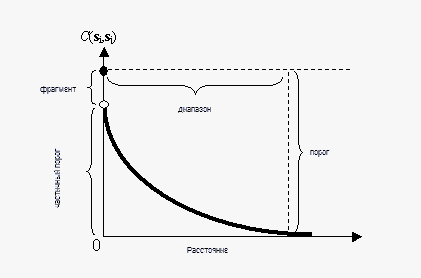
Обратите внимание, что функция ковариации уменьшается с расстоянием, поэтому ее можно рассматривать как функцию сходства.
Отношение между вариограммой и функцией ковариации
Между вариограммой и функцией ковариации имеется связь.
γ(si, sj) = sill - C(si, sj),Эту связь можно видеть на рисунках. Из-за этой эквивалентности можно сделать интерполяцию в ArcGIS Geostatistical Analyst Extension с использованием какой-либо из этих функций. (Все вариограммы в ArcGIS Geostatistical Analyst Extension имеют пороги).
Вариограммы и ковариации не могут быть только функцией. Чтобы интерполяции имели неотрицательные стандартные ошибки кригинга, в качестве вариограмм и ковариаций могут использоваться только некоторые функции. ArcGIS Geostatistical Analyst Extension предлагает несколько приемлемых вариантов, и для данных можно попробовать использовать разные варианты. Можно также иметь модели, составленные добавлением нескольких моделей – такое построение предоставляет допустимые модели, и в ArcGIS Geostatistical Analyst Extension можно добавить до четырех из них. Имеется несколько случаев, когда существуют вариограммы, но функции ковариации – нет. Например, имеется линейная вариограмма, но у нее нет порога, и нет соответствующей функции ковариации. В ArcGIS Geostatistical Analyst Extension используются модели только с порогами. Отсутствуют надежные правила выбора "наилучшей" модели вариограммы. Рассматривая эмпирическую вариограмму или функцию ковариации, можно выбрать наиболее подходящую модель. Можно также в качестве руководства использовать проверку и перекрестную проверку.