Реляционные функции используют предикаты, чтобы проверять различные типы пространственных отношений. В проверках сравниваются отношения между следующими сущностями:
- Внешняя часть геометрии (E – exterior), то есть все пространство, незанятое этой геометрией
- Внутренняя часть геометрии (I – interior), то есть все пространство, занятое этой геометрией
- Граница геометрии (B – boundary), то есть раздел между внутренней и внешней частью
Предикаты проверяют отношения. Если при сравнении выполняется критерий функции, они возвращают значение 1 или t (TRUE); в противном случае, они возвращают 0 или f (FALSE). Предикаты, проверяющие пространственные отношения, могут сравнивать пары геометрий различных типов и измерений.
Предикаты сравнивают координаты X и Y указанных геометрий. Если имеются также координаты Z или значения измерений (M), они игнорируются. Геометрии, имеющие координаты Z или измерения M, могут сравниваться с теми, которые их не имеют.
Пространственно расширенная модель девяти пересечений (DE-9IM, Dimensionally Extended 9 Intersection Model), разработанная Клементини с соавт., является расширением модели девяти измерений Эгенхофера и Герринга. Эта математическая модель DE-9IM определяет пространственные отношения между парами геометрий различных типов и измерений. В этой модели пространственные отношения между геометриями любых типов сведены к попарным пересечениям их внешней части, внутренней части и границы. В ней принимается во внимание размерность полученного пересечения.
Допустим, даны геометрии a и b. Тогда I(a), B(a) и E(a) означают внутреннюю часть, границу и внешнюю часть геометрии a, тогда как I(b), B(b) и E(b) означают то же для геометрии b. Попарные пересечения I(a), B(a) и E(a) с I(b), B(b) и E(b) образуют матрицу три-на-три. Каждое пересечение может привести к геометриям различных размерностей. Например, пересечение границ двух полигонов может состоять из точки и последовательности линий, в этом случае функция dim (функция измерений) вернет максимальную размерность, равную 1.
Функция измерений возвращает значения -1, 0, 1 и 2. Значение -1 соответствует множеству Null, возвращаемому в случае отсутствия пересечения или при dim(Ø).
| Внутренняя часть | Граница | Внешняя часть | |
|---|---|---|---|
Внутренняя часть | dim(пересечение I(a) с I(b)) | dim(пересечение I(a) с B(b)) | dim(пересечение I(a) с E(b)) |
Граница | dim(пересечение B(a) с I(b)) | dim(пересечение B(a) с B(b)) | dim(пересечение B(a) с E(b)) |
Внешняя часть | dim(пересечение E(a) с I(b)) | dim(пересечение E(a) с B(b)) | dim(пересечение E(a) с E(b)) |
Результаты предикатов пространственного отношения могут быть оценены путем сравнения их с шаблонной матрицей, содержащей возможные значения для модели DE-9IM.
Шаблонная матрица показывает, какие значения приемлемы для каждой ячейки матрицы. Возможные значения шаблонов:
T — должно существовать пересечение; dim = 0, 1 или 2
F — не должно существовать пересечения; dim = -1
* — не имеет значения, существует ли пересечение; dim = -1, 0, 1 или 2
0 — должно существовать пересечение с максимальной размерностью 0; dim = 0
1 — должно существовать пересечение с максимальной размерностью 1; dim = 1
2 — должно существовать пересечение с максимальной размерностью 2; dim = 2
Каждый предикат имеет, по меньшей мере, одну шаблонную матрицу; некоторые требуют несколько матриц для описания отношений между различными сочетаниями типов геометрии.
Шаблонная матрица предиката ST_Within (отношение "в пределах") для различных сочетаний геометрий имеет следующую форму:
b | ||||
Внутренняя часть | Граница | Внешняя часть | ||
Внутренняя часть | T | * | F | |
a | Граница | * | * | F |
Внешняя часть | * | * | * |
Проще говоря, предикат ST_Within возвращает значение TRUE, когда внутренние части обеих геометрий пересекаются, а внутренняя часть и граница a не пересекает внешнюю часть b. Все другие условия не важны.
Далее приводится описание различных предикатов, используемых при проверке пространственных отношений. На сопроводительных иллюстрациях первая входная геометрия изображена черным цветом, а вторая – оранжевым.
ST_Contains
ST_Contains ("содержит") возвращает 1 или t (TRUE), если вторая геометрия полностью содержится внутри первой геометрии. Предикат ST_Contains возвращает результаты, полностью противоположные предикату ST_Within ("в пределах").
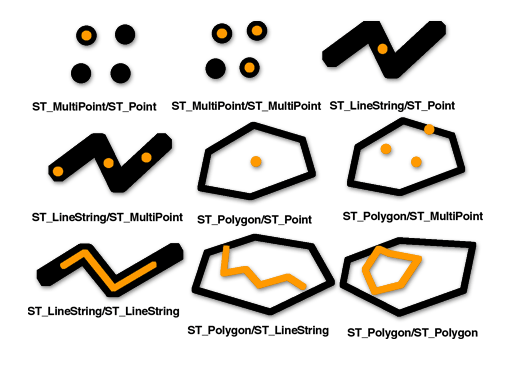
Шаблонная матрица предиката ST_Contains говорит о том, что внутренние части геометрий должны пересекаться, а внутренняя часть и граница второй (геометрия b) не должна пересекать внешнюю часть первой (геометрия a).
b | ||||
Внутренняя часть | Граница | Внешняя часть | ||
Внутренняя часть | T | * | * | |
a | Граница | * | * | * |
Внешняя часть | F | F | * |
Использование предикатов ST_Within и ST_Contains выявляет только геометрии, полностью попадающие в пределы другой геометрии. Таким образом можно исключить из выборки пространственные объекты, которые могут исказить результаты. В нижеприведенном примере продавец мороженого в передвижном фургончике хочет определить, в каких районах живет наибольшее количество детей (потенциальных покупателей), чтобы ограничить свой маршрут этими районами. Он сравнивает полигоны исследуемых районов с районами переписи, имеющими атрибут, отвечающий за общее число детей до 16 лет.
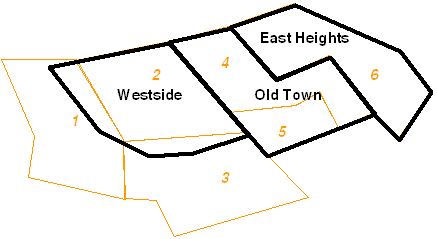
Не все дети из районов переписи 1 и 3 живут на тех участках земли, что попадают в пределы района Westside. Поэтому включение этих районов переписи в выборку приведет к искажению числа детей в районе Westside. Указав, что в выборку должны быть включены только те районы переписи, которые находятся в пределах городских районов (ST_Within = 1), мороженщик оградит себя от бесполезного блуждания по Westside и, тем самым, сэкономит свои деньги.
Синтаксис и пример использования предиката приведены в разделе ST_Contains.
ST_Crosses
ST_Crosses ("пересекает") возвращает значение 1 или t (TRUE), если геометрия, полученная в результате пересечения, имеет размерность на один меньше, чем максимальная размерность обеих исходных геометрий, и множество пересечения является внутренней частью для обеих этих геометрий. ST_Crosses возвращает 1 или t (TRUE) только при сравнении геометрий следующих типов: ST_MultiPoint/ST_Polygon, ST_MultiPoint/ST_LineString, ST_Linestring/ST_LineString, ST_LineString/ST_Polygon и ST_LineString/ST_MultiPolygon.
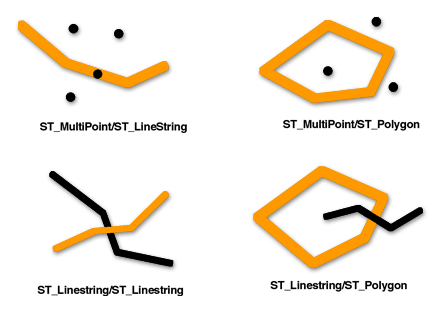
Данная шаблонная матрица предиката ST_Crosses действительна для типов ST_MultiPoint/ST_LineString, ST_MultiPoint/ST_MultiLineString, ST_MultiPoint/ST_Polygon, ST_MultiPoint/ST_MultiPolygon, ST_LineString/ST_Polygon и ST_LineString/ST_MultiPolygon. В матрице утверждается, что внутренние части должны пересекаться и, по меньшей мере, внутренняя часть первой (геометрия a) должна пересекать внешнюю часть второй (геометрия b).
b | ||||
Внутренняя часть | Граница | Внешняя часть | ||
Внутренняя часть | T | * | T | |
a | Граница | * | * | * |
Внешняя часть | * | * | * |
Данная шаблонная матрица ST_Crosses действительна для типов ST_LineString/ST_LineString, ST_LineString/ST_MultiLineString и ST_MultiLineString/ST_MultiLineString. В матрице утверждается, что размерность пересечения внутренних частей должна быть 0 (пересечение в точке). Если размерность пересечения равна 1 (пересечение по линии), предикат ST_Crosses вернет значение FALSE, но зато предикат ST_Overlaps ("перекрывает") вернет значение TRUE.
b | ||||
Внутренняя часть | Граница | Внешняя часть | ||
Внутренняя часть | 0 | * | * | |
a | Граница | * | * | * |
Внешняя часть | * | * | * |
Синтаксис и пример использования предиката приведены в разделе ST_Crosses.
ST_Disjoint
Предикат Disjoint ("разделены") вернет значение 1 или t (TRUE), если пересечение двух геометрий является пустым множеством. Другими словами, геометрии разделены, если они не пересекаются.
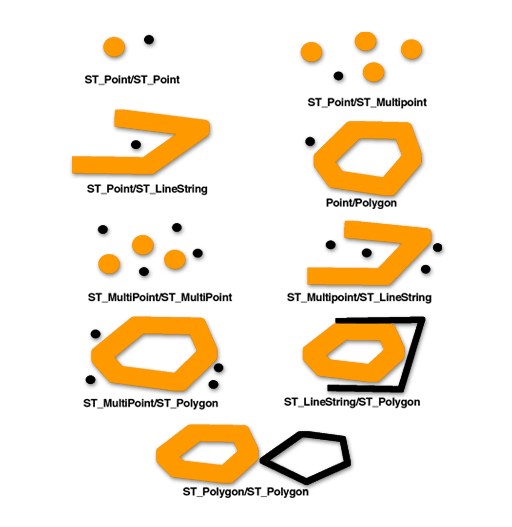
Шаблонная матрица предиката ST_Disjoint просто говорит о том, что ни внутренние части, ни границы геометрий не должны пересекаться.
b | ||||
Внутренняя часть | Граница | Внешняя часть | ||
Внутренняя часть | F | F | * | |
a | Граница | F | F | * |
Внешняя часть | * | * | * |
Синтаксис и пример использования предиката приведены в разделе ST_Disjoint.
ST_Equals
Предикат ST_Equals ("равно") возвращает значение 1 или t (TRUE), если геометрии одинаковых типов имеют идентичные координаты X, Y. Первый и второй этаж офисного здания могут иметь идентичные координаты X,Y и, следовательно, быть равными. Предикат ST_Equals также может использоваться для выявления пространственных объектов, некорректно наложенных друг на друга.
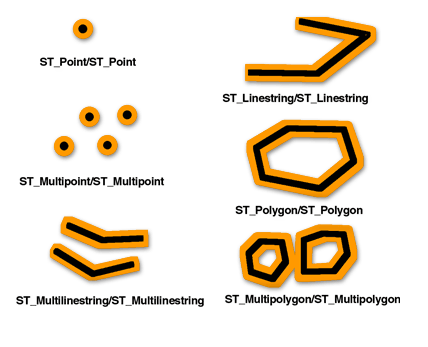
Шаблонная матрица модели DE-9IM утверждает, что геометрии равны, если их внутренние части пересекаются и никакие сегменты внутренней части или границы обеих геометрий не пересекают внешней части другой геометрии.
b | ||||
Внутренняя часть | Граница | Внешняя часть | ||
Внутренняя часть | T | * | F | |
a | Граница | * | * | F |
Внешняя часть | F | F | * |
Синтаксис и пример использования предиката приведены в разделе ST_Equals.
ST_Intersects
ST_Intersects ("пересекает") возвращает значение 1 или t (TRUE), если пересечение геометрий не является пустым множеством. ST_Intersects возвращает значение, прямо противоположное результату предиката ST_Disjoint ("разделены").
Предикат ST_Intersects возвращает TRUE, если выполняется хотя бы одна из следующих шаблонных матриц.
Предикат ST_Intersects возвращает TRUE, если внутренние части обеих геометрий пересекаются.
b | ||||
Внутренняя часть | Граница | Внешняя часть | ||
Внутренняя часть | T | * | * | |
a | Граница | * | * | * |
Внешняя часть | * | * | * |
Предикат ST_Intersects возвращает TRUE, если внутренняя часть первой геометрии пересекает границу второй геометрии.
b | ||||
Внутренняя часть | Граница | Внешняя часть | ||
Внутренняя часть | * | T | * | |
a | Граница | * | * | * |
Внешняя часть | * | * | * |
Предикат ST_Intersects возвращает TRUE, если граница первой геометрии пересекает внутреннюю часть второй геометрии.
b | ||||
Внутренняя часть | Граница | Внешняя часть | ||
Внутренняя часть | * | * | * | |
a | Граница | T | * | * |
Внешняя часть | * | * | * |
Предикат ST_Intersects возвращает TRUE, если пересекаются границы обеих геометрий.
b | ||||
Внутренняя часть | Граница | Внешняя часть | ||
Внутренняя часть | * | * | * | |
a | Граница | * | T | * |
Внешняя часть | * | * | * |
Синтаксис и пример использования предиката приведены в разделе ST_Intersects.
ST_Overlaps
ST_Overlaps ("перекрывает") сравнивает две геометрии одной размерности и возвращает 1 или t (TRUE), если множество их пересечения отлично от обеих геометрий, но имеет такую же размерность.
ST_Overlaps возвращает 1 или t (TRUE) только при сравнении геометрий одной размерности и только если множество их пересечения имеет ту же размерность. Другими словами, если пересечение двух полигонов типа ST_Polygons также является полигоном, предикат перекрытия вернет значение 1 или t (TRUE).
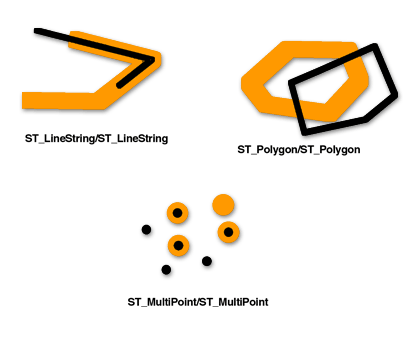
Данная шаблонная матрица действительна для перекрытия типов ST_Polygon/ST_Polygon, ST_MultiPoint/ST_MultiPoint и ST_MultiPolygon/ST_MultiPolygon. Для этих сочетаний типов предикат перекрытия вернет TRUE, если внутренняя часть обеих геометрий пересекает и внутреннюю, и внешнюю часть другой.
b | ||||
Внутренняя часть | Граница | Внешняя часть | ||
Внутренняя часть | T | * | T | |
a | Граница | * | * | * |
Внешняя часть | T | * | * |
Следующая шаблонная матрица действительна для перекрытия типов ST_LineString/ST_LineString и ST_MultiLineString/ST_MultiLineString. В этом случае пересечение геометрий должно являться геометрией размерности 1 (линиями типа ST_LineString или ST_MultiLineString). Ели размерность пересечения внутренних частей равна 0 (точка), то предикат ST_Overlaps вернет FALSE; однако предикат ST_Crosses ("пересечение") вернул бы в этом случае TRUE.
b | ||||
Внутренняя часть | Граница | Внешняя часть | ||
Внутренняя часть | 1 | * | T | |
a | Граница | * | * | * |
Внешняя часть | T | * | * |
Синтаксис и пример использования предиката приведены в разделе ST_Overlaps.
ST_Relate
ST_Relate ("связаны") возвращает значение 1 или t (TRUE), если пространственное отношение, заданное шаблонной матрицей, является корректным. Значение 1 или t (TRUE) показывает, что между геометриями существует какое-либо пространственное отношение.
Если внутренние части или границы геометрий a и b каким-либо образом связаны, предикат ST_Relate вернет значение TRUE. Пересечения внешней части одной геометрии с внутренней частью или границей другой не важны.
b | ||||
Внутренняя часть | Граница | Внешняя часть | ||
Внутренняя часть | T | T | * | |
a | Граница | T | T | * |
Внешняя часть | * | * | * |
Синтаксис и пример использования предиката приведены в разделе ST_Relate.
ST_Touches
ST_Touches ("касается") возвращает значение 1 или t (TRUE), если никакие из общих точек геометрий не пересекают их внутренних частей. По крайней мере, одна из геометрий должна иметь тип ST_LineString, ST_Polygon, ST_MultiLineString или ST_MultiPolygon.
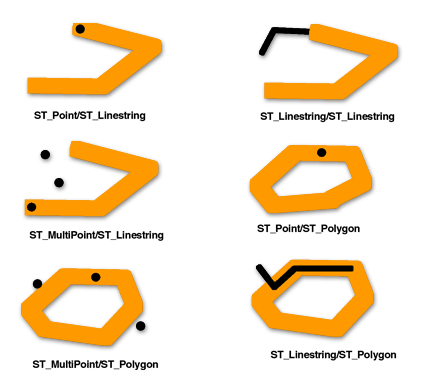
Шаблонная матрица показывает, что условие ST_Touches верно, когда внутренние части геометрий не пересекаются и граница обеих геометрий пересекает внутреннюю часть или границу другой.
Предикат ST_Touches возвращает TRUE, если граница геометрии b пересекает внутреннюю часть a, но их внутренние части не пересекаются.
b | ||||
Внутренняя часть | Граница | Внешняя часть | ||
Внутренняя часть | F | T | * | |
a | Граница | * | * | * |
Внешняя часть | * | * | * |
Предикат ST_Touches возвращает TRUE, если граница геометрии a пересекает внутреннюю часть b, но их внутренние части не пересекаются.
b | ||||
Внутренняя часть | Граница | Внешняя часть | ||
Внутренняя часть | F | * | * | |
a | Граница | T | * | * |
Внешняя часть | * | * | * |
Предикат ST_Touches возвращает TRUE, если границы обеих геометрий пересекаются, но их внутренние части не пересекаются.
b | ||||
Внутренняя часть | Граница | Внешняя часть | ||
Внутренняя часть | F | * | * | |
a | Граница | * | T | * |
Внешняя часть | * | * | * |
Синтаксис и пример использования предиката приведены в разделе ST_Touches.
ST_Within
ST_Within ("в пределах") возвращает 1 или t (TRUE), если первая геометрия полностью находится в пределах второй геометрии. Проверка ST_Within прямо противоположна проверке ST_Contains ("содержит").
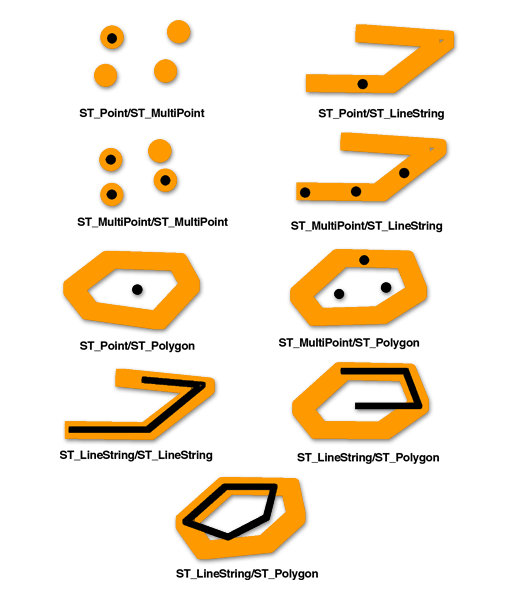
Шаблонная матрица предиката ST_Within говорит о том, что внутренние части геометрий должны пересекаться, а внутренняя часть и граница первой геометрии (геометрия a) не должна пересекать внешнюю часть второй (геометрия b).
b | ||||
Внутренняя часть | Граница | Внешняя часть | ||
Внутренняя часть | T | * | F | |
a | Граница | * | * | F |
Внешняя часть | * | * | * |
Синтаксис и пример использования предиката приведены в разделе ST_Within.