Доступно с лицензией Geostatistical Analyst.
В случае дизъюнктивного кригинга необходимы данные, имеющие двумерное нормальное распределение. Также для составления карт вероятности и квантилей предполагается, что источником данных является полное многомерное нормальное распределение. Для проверки на одномерное нормальное распределение можно использовать нормальные графики КК или гистограммы (ни одна из этих проверок не гарантирует, что исходные данные подчиняются полному многомерному нормальному распределению, но такое предположение часто является обоснованным, если эти инструменты диагностики обнаруживают одномерное нормальное распределение).
Рассмотрим следующее вероятностное высказывание:
f(p,в) = Prob[Z(ю) ≤ zp, Z(ю + в) ≤ zp],где zp – стандартный нормальный квантиль для вероятности p.
Например, знакомый стандартный нормальный квантиль – когда p = 0,975, то zp = 1,96 и когда p = 0,5, то zp = 0 и когда p = 0,025, то zp = -1,96. В приведенном выше вероятностном высказывании для переменной Z в местоположении s и другой переменной Z в другом местоположении s + h устанавливается вероятность, что они обе меньше zp. Это вероятностное выражения является функцией f(p,h), зависящей от p (и, соответственно zp) and h. Эта функция также будет зависеть от уровня автокорелляции между Z(s) и Z(s + h).
Предположим, что Z(s) и Z(s + h) имеют двумерное нормальное распределение. Если автокорреляция известна, существуют формулы для f(p, h). Пусть h – константа и меняется только p. Можно ожидать, что функция будет выглядеть следующим образом:
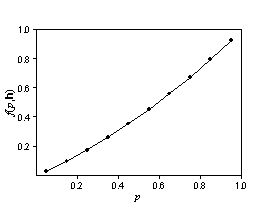
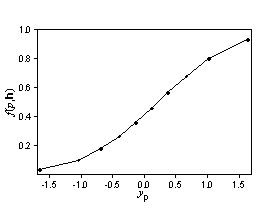
Второй рисунок выглядит как кумулятивное распределение вероятностей. Теперь допустим, что p фиксировано, а f(p,h) меняется в зависимости от h.
Пусть сначала значение h очень мало. В этом случае Prob[Z(s) ≤ zp, Z(s + h) ≤ zp] почти эквивалентно Prob[Z(s) ≤ zp] = p. Далее, предположим, что h является очень большим. В этом случае Prob[Z(s) ≤ zp, Z(s + h) ≤ zp] почти эквивалентно Prob[Z(s) ≤ zp] Prob[Z(s + h) ≤ zp] = p2 (поскольку Z(s) and Z(s + h) практически независимы). Таким образом, для фиксированного p можно ожидать, что f(p, h) будет варьироваться между p и p2. Теперь, считая f(p, h) функцией p и длины h, получим результат, подобный приведенному на следующем рисунке:
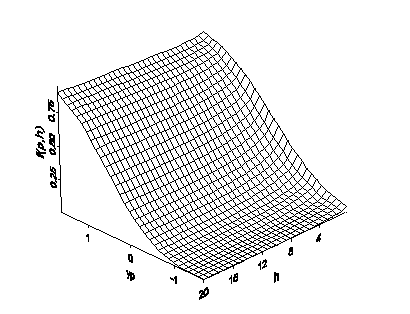
Эту функцию можно преобразовать в вариограммы и ковариационные функции для индикаторов. Prob[Z(s) ≤zp, Z(s + h) ≤zp] = E[I(Z(s) ≤zp)xI(Z(s + h) ≤zp)], где I(оператор) – индикаторная функция, которая принимает значение 1, если оператор = true, в противном случае она равна 0; тогда ковариационная функция для индикаторов при фиксированном p:
CI(в;p) = f(p,в) –p2,а вариограмма для индикаторов при фиксированном p:
γI(в;p) = p -f(p,в).Таким образом, можно рассчитать вариограмму и ковариационную функцию для индикаторов исходных данных и использовать их для получения ожидаемых вариограмм и ковариационных функций индикаторов для различных значений p.