Доступно с лицензией Geostatistical Analyst.
Некоторые методы интерполяции и имитации требуют нормального распределения входных данных (см. раздел Изучение распределения данных со списком этих методов). Преобразование по методу нормальных меток (NST) изменяет набор данных так, чтобы он приблизился к стандартному нормальному распределению. Это достигается с помощью расположения значений в наборе по возрастанию и связывания этих рядов с эквивалентными рядами, созданными с помощью нормального распределения. Шаги преобразования следующие: набор данных сортируется и располагается по возрастанию, для каждого ряда в наборе находится эквивалентный ряд из стандартного нормального распределения, значения при нормальном распределении связываются с рядами из преобразованного набора данных. Процесс сортировки можно выполнить с помощью частотного или кумулятивного распределения наборов данных.
Ниже приводятся примеры, показывающие гистограммы и функции распределения до и после преобразования по методу нормальных меток:
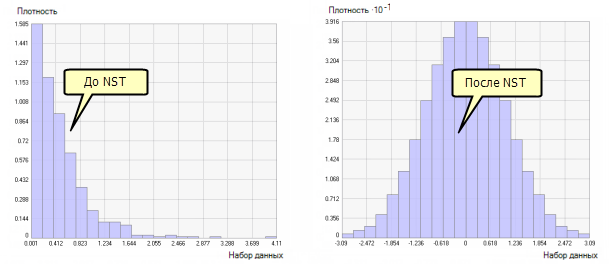
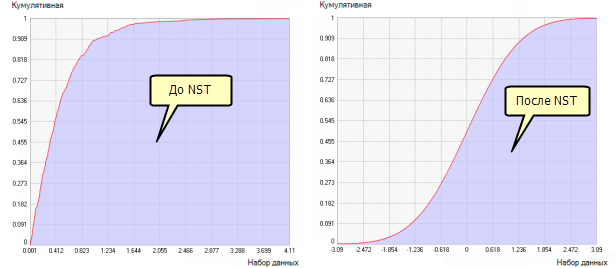
Методы аппроксимации
В ArcGIS Geostatistical Analyst Extension используются четыре метода аппроксимации: прямой, линейный, с гауссовыми ядрами и мультипликативный сдвиг. Прямой метод использует наблюдаемое кумулятивное распределение. Линейный метод соединяет отрезками шаги функции распределения. Метод с гауссовыми ядрами аппроксимирует функцию распределения, используя линейную комбинацию компонента функции нормального распределения. Мультипликативный сдвиг аппроксимирует функцию распределения, используя базовое (t Стьюдента, логнормальное, гамма-, эмпирическое и логэмпирическое) распределение, которое сдвигается подходящей линейной комбинацией бета-распределений (сдвиг завершается интегральным преобразованием обращения вероятности). Логнормальное, гамма- и логэмпирическое базовые распределения можно использовать только для положительных данных, интерполяции будут гарантированно положительными. Качество использованной модели определяется с помощью информационного критерия Акаике (AIC).
После получения прогнозных значений по методу преобразования нормальных меток они будут автоматически преобразованы назад к исходному масштабу. Выбор метода аппроксимации зависит от сделанных предположений и сглаженности аппроксимации. Прямой метод наименее сглаженный, но имеет наименьшее число предположений, линейный метод является промежуточным. Методы с использованием гауссова ядра и мультипликативного сдвига дают сглаженное обратное преобразование, но требуют допущения, что распределение данных можно аппроксимировать конечной комбинацией известных распределений.