Интерполяция ядра – это вариант преобразования первого порядка по методу локальных полиномов, в котором неустойчивость расчетов предотвращается методом, схожим с используемым в гребневой регрессии для определения коэффициентов регрессии. Оценка имеет малое смещение и гораздо точнее метода оценки без смещения, потому стоит использовать этот метод как предпочитаемый метод оценки. Подробнее о гребневой регрессии можно прочесть, например, в работе Hoerl and Kennard (1970).
Ошибка прогноза интерполяции по методу локальных полиномов оценивается с учетом допущения, что модель верна, так что пространственное число обусловленности мало везде. Это предположение часто нарушается, и пространственное число обусловленности выделяет области, где прогнозы и их среднеквадратические погрешности нестабильны. В модели со сглаживанием ядра проблема чрезмерно больших среднеквадратических погрешностей и спорных прогнозов исправляется с помощью параметра хребта, введением небольшого смещения в уравнения. Это снимает необходимость привязки пространственного числа обусловленности. Таким образом, интерполяция ядра для типа выходной поверхности дает только интерполяцию и стандартную ошибку интерполяции. Поскольку параметр хребта вводит смещение для стабилизации прогнозов, следует использовать настолько малое значение, насколько возможно при соблюдении стабильности модели. Подробнее об этом можно прочитать в статье «Local Polynomials for Data Detrending and Interpolation in the Presence of Barriers», Gribov and Krivoruchko (2010).
Еще одно различие между моделями состоит в том, что модель интерполяции ядра использует наименьшее расстояние между точками, так что точки по разным сторонам определенного непроходимого (абсолютного) барьера соединены серией прямых линий.
Интерполяция ядра использует следующие радиально-симметричные ядра: экспоненциальное, гауссово, четвертого порядка, Епанечникова, полиномиальное пятого порядка и константу. Ширина ядра определяется прямоугольником вокруг наблюдений.
Ядро Епанечникова обычно показывает лучшие результаты с полиномами первой степени. Однако в зависимости от данных, перекрестная и диагностическая проверка могут требовать другого ядра, см. Fan and Gijbels (1996).
Прогнозы интерполяции ядра с барьерами сравниваются ниже с абсолютными, левыми, правыми и без барьеров. Обратите внимание, что на рисунке слева изолинии резко меняются у барьеров, а на рисунке справа изолинии плавно переходят через них.

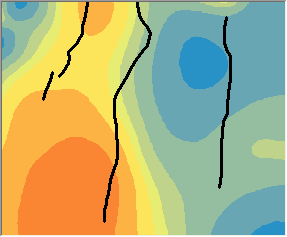
Модели, основанные на кратчайшем расстоянии между точками, предпочтительнее использовать в гидрологических и метеорологических приложениях.
Функции ядра
Функции ядра: во всех формулах, приведенных ниже, r –– радиус с центром в точке s, h – ширина канала.
- Экспоненциальные:
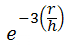
- Гауссово:
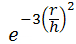
- Биквадратная

- Функция Епанечникова:

- PolynomialOrder5:
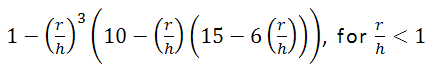
- Константа:
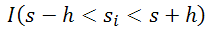
где I(expression) является индикатором функции, который принимает значение 1, если expression равно true, и 0, если expression равно false.
Параметр ширины ядра применяется ко всем функциям ядра, кроме константы. Функции ядра экспоненциальная, гауссова и константа дополнительно поддерживают сглаженную окрестность поиска для ограничения диапазона ядра.
Ссылки и дополнительная литература
Fan, J. and Gijbels, I. (1996). Local Polynomial Modelling and Its Applications, Chapman & Hall. London.
Hoerl, A.E. and Kennard, R.W. (1970), Ridge regression: biased estimation for nonorthogonal problems, Technometrics, 12, 55-67.
Yan, Xin. (2009) Linear regression analysis : theory and computing. Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224.