Доступно с лицензией Spatial Analyst.
Доступно с лицензией 3D Analyst.
Инструмент Уклон определяет крутизну в каждой ячейке растровой поверхности. Чем меньше значение уклона, тем более плоской является земная поверхность; чем больше значение уклона, тем более крутые склоны расположены на поверхности.
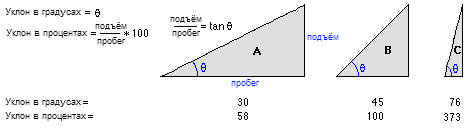
Выходной растр уклонов может быть вычислен в двух различных единицах измерения, в градусах или в процентах ('процент подъема'). Процент подъема можно лучше понять, если вы рассматриваете его как подъем, деленный на пробег (спуск), умноженный на 100. Рассмотрим треугольник B на рисунке внизу. Когда угол равен 45 градусам, подъем равен пробегу (спуску), а процент подъема равен 100 процентам. По мере того, как угол наклона приближается к вертикальному (90 градусов), как в треугольнике C, процент подъема стремится к бесконечности.
Инструмент Уклон чаще всего работает с набором данных высот, как показано на следующих рисунках. Более крутые уклоны заштрихованы красным на выходном растре уклона.
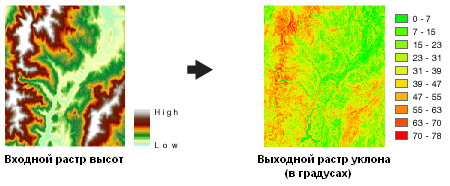
Инструмент также может использоваться с другими типами непрерывных данных, например, численность населения, для выявления резких изменений значения.
Методы вычисления и эффект ребер
Для вычисления уклона доступно два метода. Вы можете выбрать метод вычисления Плоскостной или Геодезический, используя параметр Метод.
Для плоскостного метода, уклон измеряется как максимальное соотношение изменения значений ячейки и ее непосредственного окружения. Расчет выполняется на проецированной плоскости при использовании декартовой системы координат 2D. Значение уклона вычисляется с использованием методики усредненного максимума (Burrough, 1998).
По геодезическому методу вычисления будут выполняться в декартовой системе координат 3D учетом формы земной поверхности в виде эллипсоида. Значение уклона вычисляется измерением угла между топографической поверхностью и базовым датумом.
Плоскостные и геодезические вычисления выполняются с помощью окрестности размером 3 на 3 ячейки (плавающее окно). Для каждой окрестности, если обрабатываемая (центральная) ячейка имеет значение NoData, выходное значение будет NoData. Для вычислений также необходимо, чтобы не менее семи окрестных ячеек имели допустимые значения. Если менее семи ячеек имеют корректные значения, вычисление не производится, а выходным значением обрабатываемой ячейки будет NoData.
Ячейки в наиболее удаленных строках и столбцах выходного растра получат значение NoData. Это происходит потому, что вдоль границы входного набора данных у ячеек нет достаточного количества соседей.
Плоскостной метод
Для каждой ячейки инструмент вычисляет максимальную степень изменения в значении z между конкретной ячейкой и соседними с ней ячейками. По сути, максимальная степень изменения в значениях высоты на единицу расстояния между ячейкой и восемью соседними с ней ячейками определяет самый крутой спуск вниз по склону из ячейки.
Алгоритм вычисления плоскостного уклона
Уклон определяет степень изменения (дельту) поверхности в горизонтальном (dz/dx) и вертикальном (dz/dy) направлениях из центральной ячейки. Базовый алгоритм, используемый для вычисления уклона, выглядит так:
slope_radians = ATAN ( √ ([dz/dx]2 + [dz/dy]2) )Уклон обычно измеряется в градусах с использованием следующего алгоритма:
slope_degrees = ATAN ( √ ([dz/dx]2 + [dz/dy]2) ) * 57.29578Алгоритм уклона может быть проинтерпретирован также следующим образом:
slope_degrees = ATAN (rise_run) * 57.29578- где:
rise_run = √ ([dz/dx]2 + [dz/dy]2]
Горизонтальную и вертикальную дельты определяют значения центральной ячейки и восьми соседних с ней ячеек. Соседние ячейки обозначаются буквами от a до i, при этом буква e обозначает ячейку, для которой вычисляется уклон.

Степень изменения по направлению x для ячейки 'e' вычисляется с помощью следующего алгоритма:
[dz/dx] = ((с + 2f + i)*4/wght1 - (a + 2d + g)*4/wght2) / (8 * x_cellsize)- где:
wght1 и wght2 являются горизонтально взвешенным числом корректных ячеек.
Например, если:
- c, f и i имеют корректные значения, wght1 = (1+2*1+1) = 4.
- i является NoData, wght1 = (1+2*1+0) = 3.
- f является NoData, wght1 = (1+2*0+1) = 2.
Аналогичная логика применяется к wght2, за исключением того, что соседними местоположениями являются a, d и g.
Степень изменения по направлению y для ячейки 'e' вычисляется с помощью следующего алгоритма:
[dz/dy] = ((g + 2h + i)*4/wght3 - (a + 2b + с)*4/wght4) / (8 * y_cellsize)- где:
wght3 и wght4 имеют ту же концепцию, что и в вычислении [dz/dx].
Пример вычисления плоскостного уклона
В качестве примера будет вычислено значение уклона центральной ячейки скользящего окна.
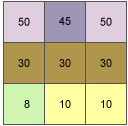
Степень изменения для центральной ячейки 'e' по направлению x:
[dz/dx] = ((с + 2f + i)*4/wght1 - (a + 2d + g)*4/wght2) / (8 * x_cellsize) = ((50 + 60 + 10)*4/(1+2+1) - (50 + 60 + 8)*4/(1+2+1)) / (8 * 5) = (120 - 118) / 40 = 0.05Степень изменения для центральной ячейки 'e' по направлению y:
[dz/dy] = ((g + 2h + i)*4/wght3 - (a + 2b + с)*4/wght4) / (8 * y_cellsize) = ((8 + 20 + 10)*4/(1+2+1) - (50 + 90 + 50)*4/(1+2+1)) / (8 * 5) = (38 - 190 ) / 40 = -3.8Учитывая степень изменения в направлении x и y, уклон для центральной ячейки e вычисляется с использованием следующего алгоритма:
rise_run = √ ([dz/dx]2 + [dz/dy]2) = √ ((0.05)2 + (-3.8)2) = √ (0.0025 + 14.44) = 3.80032 slope_degrees = ATAN (rise_run) * 57.29578 = ATAN (3.80032) * 57.29578 = 1.31349 * 57.29578 = 75.25762Целочисленное значение уклона для ячейки 'e' составляет 75 градусов.
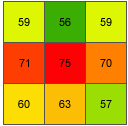
Геодезический метод
При геодезическом методе уклон поверхности измеряется в геоцентрической 3D системе координат – также называющейся системой координат Earth Centered, Earth Fixed (ECEF) – с учетом эллипсоидной формы земли. Проекция набора данных на результаты вычислений не влияет. При этом используются единицы измерения z входного растра, если они заданы в пространственной привязке. Если в пространственной привязке входных данных не заданы единицы измерения z, необходимо сделать это с помощью параметра задания z-единиц. Геодезический метод дает более точный результат, чем плоскостной.
Преобразование геодезических координат
Система координат ECEF является 3D правосторонней Декартовой системой координат с центром земли в качестве начальной точки, в которой любое местоположение представлено координатами X, Y и Z. На следующем рисунке приводится пример целевого местоположения T, выраженного в геоцентрических координатах.

В геодезических вычислениях используются координаты X, Y, Z, которые вычисляются на основе геодезических координат(широта φ, долгота λ, высота h). Если система координат входного растра поверхности является системой координат проекции, растр сначала перепроецируется в географическую систему координат, в которой каждое местоположение имеет геодезические координаты, затем он преобразуется в систему координат ECEF. Высота h (z-значение) является эллипсоидной высотой, основанной на поверхности эллипсоида. См. иллюстрацию ниже.

Для преобразования геодезических координат (широта φ, долгота λ, высота h) в координаты ECEF используются следующие формулы:
X = (N(φ)+h)cosφcosλY = (N(φ)+h)cosφsinλZ = (b2/a2*N(φ)+h)sinφ- , где:
- N( φ ) = a2/ √(a2cosφ2+b2sinφ2)
- φ = широта
- λ = долгота
- h = эллипсоидальная высота
- a = большая полуось эллипсоида
- b = малая полуось эллипсоида
Эллипсоидная высота h в следующих формулах дается в метрах. Если z-значения входного растра даны в других единицах измерения, они будут преобразованы в метры.
Вычисление уклона
Геодезический уклон является углом между топографической поверхностью и поверхностью эллипсоида. Любая поверхность, параллельная поверхности эллипсоида, имеет уклон 0. Чтобы вычислить уклон в каждом местоположении, вокруг обрабатываемой ячейки создается плоскость окрестности размером 3 x 3 ячейки, по методу наименьших квадратов. Наилучшее соответствие по методу наименьших квадратов минимизирует сумму квадратов разницы (dzi) между реальным и подобранным z-значением. Пример приведен на рисунке ниже.

Здесь плоскость представлена в виде z = Ax + By + C. Для каждого центра ячейки, dzi является разницей между реальным z-значением и подобранным.
Наилучшее соответствие плоскости достигается, когда ∑9i=1dzi2 минимальна.
После подгонки плоскости, в местоположении ячейки вычисляется нормаль к поверхности. В том же местоположении вычисляется нормаль эллипсоида, перпендикулярная плоскости, проходящей по касательной к поверхности эллипсоида.
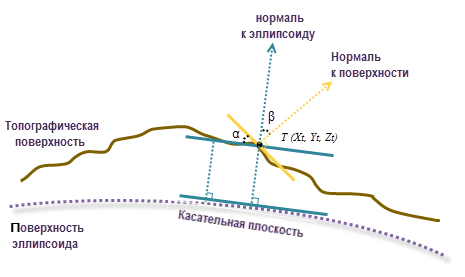
Уклон, в градусах, вычисляется по углу между нормалью к эллипсоиду и нормалью к топографической поверхности, который здесь обозначается как β. Согласно рисунку выше, угол α является геодезическим уклоном, что соответствует углу β, согласно закону подобной геометрии.
Для вычисления уклона в процентах используется следующая формула:
Slope_PercentRise = ATAN(β) * 100%Использование графического процессора (GPU)
При использовании геодезического метода, производительность инструмента значительно повышается если используются GPU определенных моделей. Дополнительные сведения о поддержке этого механизма, его настройке и включении см. в разделе Работа GPU с Spatial Analyst.
Справочная информация
Burrough, P. A., and McDonell, R. A., 1998. Principles of Geographical Information Systems (Oxford University Press, New York), 190 pp.
Marcin Ligas, and Piotr Banasik, 2011. Conversion between Cartesian and geodetic coordinates on a rotational ellipsoid by solving a system of nonlinear equations (GEODESY AND CARTOGRAPHY), Vol. 60, No 2, 2011, pp. 145-159
B. Hofmann-Wellenhof, H. Lichtenegger and J. Collins, 2001. GPS - theory and practice. Section 10.2.1. p. 282.
David Eberly 1999. Least Squares Fitting of Data (Geometric Tools, LLC), pp. 3.