需要 Geostatistical Analyst 许可。
通过探索数据,您将能够更好地了解测量值之间的空间自相关。这种了解有助于在选择空间预测模型时做出更好的决策。
空间自相关
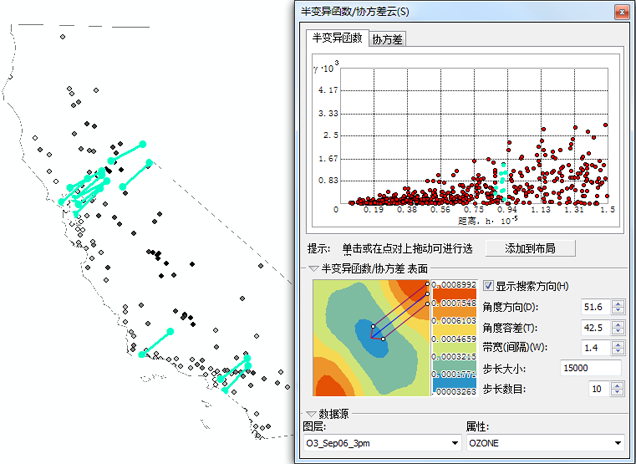
可通过检查不同的采样位置对来探索数据的空间自相关。通过测量两个位置间的距离并绘制这些位置上的值之间的差值平方,可创建半变异函数云。x 轴表示各位置间的距离,y 轴表示这些位置上的值的差值平方。半变异函数中的每个点都表示一个位置对,而不是地图上的单个位置。
如果存在空间相关性,则距离较近的点对(在 x 轴的最左侧)应具有较小的差值(在 y 轴上的值较小)。随着各个点之间的距离越来越大(点在 x 轴上向右移动),通常,差值的平方也应随之增大(在 y 轴上向上移动)。通常,平方差超过某个距离后就会保持不变。超过这个距离的位置对被视为不相关。
地统计方法的基本假设是,对于任意两个彼此间的距离和方向都相近的位置,其差值的平方也应相近。这种关系称为平稳性。
空间自相关可能仅依赖于两个位置之间的距离,这被称为各向同性。不过,考虑不同的方向时,对于不同的距离,可能出现相同的自相关值。其另一种理解是,对于较长的距离,事物在某些方向上比在其他方向上更相似。半变异函数和协方差中都存在这种方向性影响,它被称为各向异性。
查找各向异性很重要,这是因为如果在自相关中检测到方向上的差异,就可以在半变异函数或协方差模型中考虑这些差异。这反过来又会对地统计预测产生影响。
利用“半变异函数/协方差云”工具探索空间结构
半变异函数/协方差云工具可用于研究数据集的自相关。接下来,让我们考虑一下臭氧数据集。注意:在下图中,您可以选择相隔一定距离的所有位置对,方法是在半变异函数云中擦除在那个距离上的所有点。
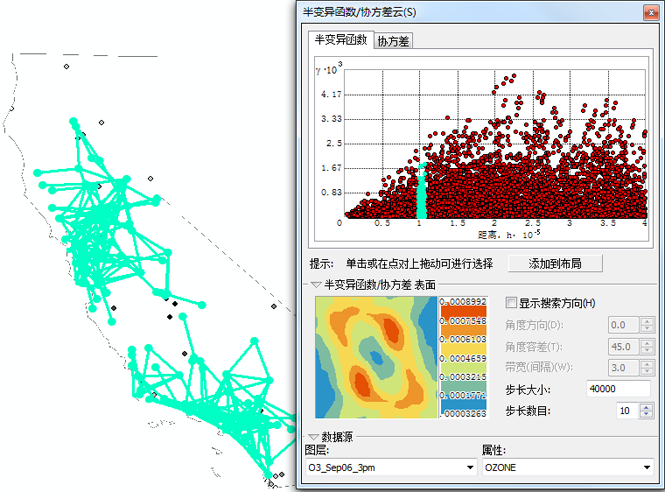
利用“半变异函数/协方差云”工具查找方向影响
在前面的示例中,使用了“半变异函数/协方差云”工具来查看数据的全局自相关。不过,查看半变异函数表面时,半变异函数的值中可能存在方向差异。单击显示搜索方向并设置角度和带宽时(如下图所示),将会看到连在一起的位置具有非常类似的值,这是因为半变异函数的值相对较小。
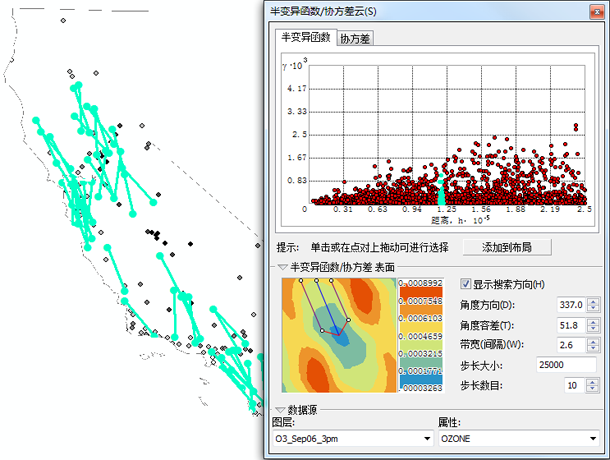
如果更改链接的方向(如下图所示),将会看到一些连在一起的位置具有非常不同的值,这会使得半变异函数的值很大。这表明通常情况下,东北方向上相距 125000 米的位置比西北方向上的位置的差异更大。回想一下,当一个方向上的变化改变得比另一个方向上的快时,这种现象称为各向异性。利用 Geostatistical Analyst 向导对表面进行插值时,可使用考虑到各向异性的半变异函数模型。