扩散插值指热方程的基本解,该方程描述热或粒子如何在同类介质中随着时间扩散。使用此方法得到的预测结果缓慢地在障碍周围流动。
在没有障碍的情况下,通过扩散插值得到的预测结果与通过使用高斯核的核插值法得到的预测结果大致相同。
扩散插值可以使用通过成本面定义的复制的距离度量,它是一个常用栅格函数,用于计算从一个栅格像元到另一个栅格像元的行程成本。
扩散插值为自动选择的格网(像元)生成预测结果,而 Geostatistical Analyst 中的所有其他模型使用大小可变的三角形。
如果未指定成本面,相邻像元中心之间的距离为欧氏距离。如果已经指定成本面,则使用以下公式之一定义成本面上像元之间的距离:
- 附加障碍
(相邻像元的平均成本值)x(像元中心间的距离)
- 累积障碍
(相邻单元的成本值之差)+(单元中心间的距离)
- 流动障碍
指示符(至相邻像元的成本值 > 自相邻像元的成本值)*(至相邻像元的成本值 - 自相邻像元的成本值)+(像元中心间的距离)
其中,Indicator(True) = 1,Indicator(False) = 0。
流动障碍可用于使用数据变化的主方向插入数据。
可将下图左侧没有成本面的“含障碍的扩散插值”结果与下图右侧使用“含障碍的核插值法”创建的预测图相比较。
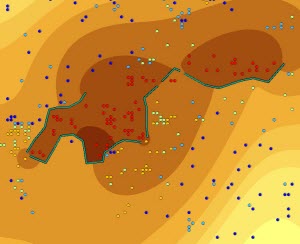
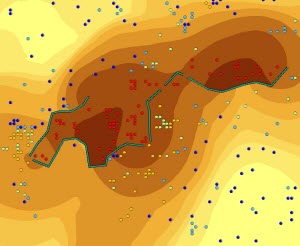
在扩散插值的情况下,核的形状根据扩散方程在障碍附近变化;而在核插值的情况下,点之间的距离根据点之间的最短距离变化。
有关此主题的反馈?