在执行移动窗口克里金法之前,必须使用克里金方法创建一个地统计图层,而不能使用协同克里金法和经验贝叶斯克里金法创建。
可对克里金法的参数进行调整,也可以将其保留为克里金方法自动确定的初始默认值。移动窗口克里金法的基本原理是根据较小的邻域重新计算变程、块金和偏基台半变异函数参数。
如果数据不稳定,可以估计异类半变异函数。换句话说,使用位于待预测位置中心的移动窗口并为每个局部邻域创建半变异函数。
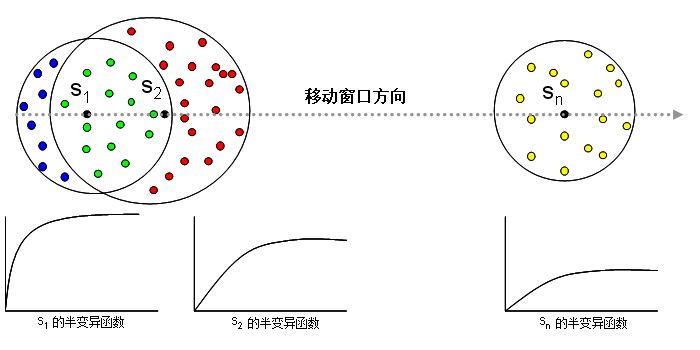
研究区域中每个点的预测值可按顺序映射为穿过研究区域的窗口(图 1)。此例中,数据在旋转时是各向同性的或是恒定的。为完全映射研究区域中的每个位置,会计算每个待预测位置的半变异函数。在每个邻域中,假定数据在局部是稳定的,所以不违反克里金算法的假设条件。
在窗口穿过研究区域时,使用邻近点计算新的半变异函数参数。对于位置 s1,蓝点和绿点在空间上是相关的,或在以该点为圆心的圆的半径所表示的变程距离以内。对于位置 s2,绿点和红点在空间上是相关的,而对于位置 sn,黄点在空间上是相关的。可使用该方法查看数据的空间结构是如何在研究区域内更改的。如果半变异函数在不同窗口中并未发生大量更改,则表示数据接近稳态,适合使用稳态的克里金模型。但是,如果半变异函数在移动窗口间发生了显著的更改,则表示数据并非处于稳态,不适合使用稳态的克里金模型。