需要 Geostatistical Analyst 许可。
半变异函数显示测量采样点的空间自相关。绘制每对位置(经验半变异函数分组),然后根据这些位置拟合模型(将模型与经验半变异函数拟合)。通常使用某几个特征来描述这些模型。
变程和基台
查看半变异函数的模型时,您将注意到模型会在特定距离处呈现水平状态。模型首次呈现水平状态的距离称为变程。比该变程近的距离分隔的样本位置与空间自相关,而距离远于该变程的样本位置不与空间自相关。
半变异函数模型在变程处所获得的值(y 轴上的值)称为基台。偏基台等于基台减去块金。
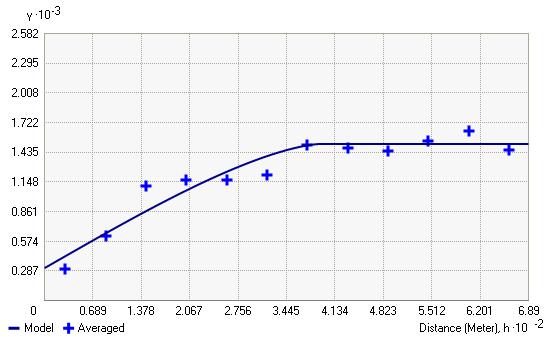
块金
从理论上讲,在零间距(步长 = 0)处,半变异函数的值是 0。但是,在极小的间距处,半变异函数通常显示块金效应,即值大于 0。例如,如果半变异函数模型在 y 轴上的截距为 2,则块金为 2。
块金效应可以归因于测量误差或小于采样间隔距离处的空间变化源(或两者)。由于测量设备中存在固有误差,因此会出现测量误差。自然现象可随着比例范围变化而产生空间变化。小于样本距离的微刻度变化将表现为块金效应的一部分。收集数据之前,能够理解空间变化的比例非常重要。