需要 Geostatistical Analyst 许可。
协同克里金法使用多种变量类型的信息。主要的感兴趣变量是 Z1,可利用 Z1 的自相关性和 Z1 与所有其他变量类型间的互相关性进行更好的预测。使用其他变量的信息进行预测固然很好,但也有其弊端。协同克里金法需要进行更多的估计,包括估计每一变量的自相关性以及所有的互相关性。从理论上讲,克里金法最保险,因为即使没有互相关性,也可以对 Z1 的自相关性进行估计。但是,每一次对未知自相关参数进行估计都会产生更多的变化,从而使得为获得精确性作出的努力得不偿失。
普通协同克里金法对模型做了假设
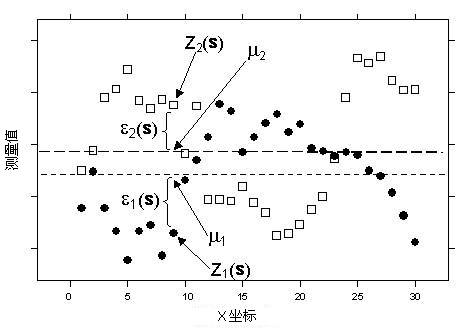
Z1(s) = µ1 + ε1(s) Z2(s) = µ2 + ε2(s),其中,µ1 和 µ2 为未知常量。请注意,此时存在两种类型的随机误差,ε1(s) 和 ε2(s),因此,它们各自具有自相关性且两者之间存在互相关性。同普通克里金法一样,普通协同克里金法尝试对 Z1(s0) 进行预测,但是为了使预测更精确,还使用了协变量 Z2(s) 中的信息。例如,下图中的数据与普通克里金法使用的数据相同,只是在此处额外添加了另外一个变量。
请注意,数据 Z1 和 Z2 具有自相关性。还应注意,当 Z1 低于其平均值 µ1 时,Z2 往往会高于其平均值 µ2,反之亦然。因此,Z1 和 Z2 具有负的互相关性。在本例中,每一位置 s 都有对应的 Z1(s) 和 Z2(s);但这是不必要的,每一变量类型都可以具有其自身独特的一组位置。主要的感兴趣变量是 Z1,自相关性和互相关性都用来进行更好的预测。
其他协同克里金法 - 泛协同克里金法、简单协同克里金法、指示协同克里金法、概率协同克里金法和析取协同克里金法 - 为上述方法的扩展方法,适用于有多个数据集的情况。例如,可通过以下方式实现指示协同克里金法:为数据使用多个阀值,而后使用每个阀值的二进制数据来预测主要感兴趣的阀值。因此,指示协同克里金法与概率克里金法类似,但前者对异常值和其他不稳定数据敏感度较低。
协同克里金法可以使用半变异函数或协方差(用于表示自相关性的数学形式)、互协方差(用于表示互相关性的数学形式)和变换以及趋势移除;并在执行普通协同克里金法、简单协同克里金法或泛协同克里金法时允许存在测量误差。