克里金模型可以生成何种类型的输出表面？

需要 Geostatistical Analyst 许可。

克里金法和协同克里金法都是预测方法，最终目标是生成一个预测值表面。而且，您可能还会希望了解预测值的准确性。可生成三种不同类型的预测图，其中的两种关联有标准误差。您可选择按模型组织克里金方法；而本章节将按目标对它们进行组织。考虑下图，假定三个位置的预测都为正态分布：

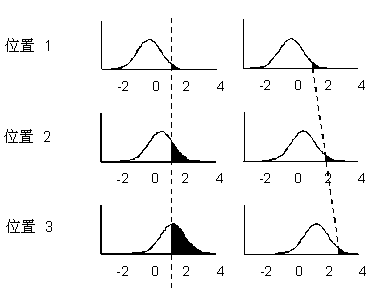
预测将位于每条曲线的中心，同时可为整个表面生成预测图。观察左侧的三个图，如果要预测值大于阈值 1（举例来说）的要素概率，可计算曲线下虚线右侧的面积。每个位置的预测分布都不同。因此在保持阈值恒定时，将为整个表面生成概率图。观察右侧的三个图，如果要预测值概率为 5% 的分位数，请计算虚线上的值（取自 x 轴）。同样，每个位置的预测分布都不同。因此在保持概率恒定时，将为整个表面生成分位数图。可为预测图和概率图生成标准误差图。下表给出各种方法和输出图以及主要假设条件：

克里金法和协同克里金法	预测	预测标准误差	分位数图	概率图	标准误差指示图
普通克里金	X	X	X*	X*
泛克里金	X	X	X*	X*
简单克里金	X	X	X*	X*
指示克里金				X	X
概率				X	X
析取克里金	X**	X**		X**	X**
经验贝叶斯	X	X	X*	X*
面插值	X	X

克里金方法和输出图表

*要求多元正态分布假设条件

**要求成对二元正态假设条件

• 了解有关不同克里金模型的信息

有关此主题的反馈?