中位数中心工具是一种对异常值反应较为稳健的中心趋势的量度。该工具可标识数据集中到其他所有要素的行程最小的位置点。例如,对紧凑性群集点的平均中心进行计算的结果是该群集中心处的某个位置点。如果随后添加一个远离该群集的新点并重新进行计算平均中心,您会注意到结果会向新的异常值靠近。而如果要使用中位数中心工具执行相同的测试,您会发现新的异常值对结果位置的影响明显减小。中位数中心工具可指定权重字段。您可将权重视为与每个要素关联的行程个数(例如,如果要素的权重为 3.2,则行程数将为 3.2)。加权中位数中心是所有行程的距离之和最小的位置点。
用于计算中位数中心的方法是一个迭代过程,由 Kuhn 和 Kuenne (1962) 提出,之后在 Burt 和 Barber (1996) 中进一步概括。在算法的每个步骤 (t) 中,都会找到一个候选“中位数中心”(Xt, Yt),然后对其进行优化,直到其表示的位置距数据集中的所有要素(或所有加权要素)(i) 的“欧式距离”d 最小。
计算
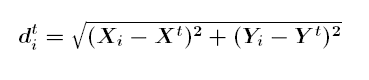
输出
中位数中心工具可创建具有一个中位数中心点要素的输出要素类,或者如果指定了案例分组字段,则可为每个案例创建一个点要素。X 和 Y 中位数中心值、案例及属性字段中值(属性字段中的各字段)都作为输出要素类中的属性。各属性字段的值是对应字段的所有字段值进行计算所获得的中位数值。一组数值的中位数是它的中间值:数据集中有 1/2 的值小于该值,而另外 1/2 的值大于该值。
可能的应用
如果需要一个对于空间异常值反应比较稳健的中心趋势的量度值,则可以使用中位数中心工具。例如,如果不希望少数外围火灾使得实际的中心位置远离火灾核心区,则可以使用该工具计算火灾区的“中位数中心”。通常,对平均中心与中位数中心的结果进行比较来查看外围要素对最终结果的影响是十分有趣的。对于许多应用,与“平均中心”相比,“中位数中心”是一种更为典型的中心趋势量度。
其他资源
以下参考资料中包含了有关此工具的详细信息:
Burt, J. E., and G. Barber. (1996).Elementary statistics for geographers.Guilford, New York.
Kuhn, H. W., and R. E. Kuenne (1962).An efficient algorithm for the numerical solution of the Generalized Weber Problem in spatial economics.Journal of Regional Science, 4(2):21–33.