需要 Spatial Analyst 许可。
模糊逻辑可用作叠加分析方法,来求解诸如地点选择和适宜性模型等传统的叠加分析应用。
模糊逻辑的基本前提是空间数据的属性和几何中存在误差。模糊逻辑提供了用于解决两种类型的误差的方法,但由于模糊逻辑与叠加分析相关,因此其重点关注的是属性数据中的误差。类的定义以及现象的测量值中是属性数据中出现误差的两个主要方面。这两种误差源(尤其在类的定义中)可在将像元指定给特定类时造成不精确的结果。
分类中各个类的定义以及将现象指定给各个类时的不精确性可影响决策的制定。“模糊叠加”工具可帮助决策者指定这些与不精确性相关的决策。模糊逻辑重点在于对类边界的不准确性进行建模。
加权叠加和加权总和工具基于明确集合,其中每个像元在或不在某个类中。模糊逻辑专门用于解决各个类之间的边界不明确时的情况。与明确集合不同,模糊逻辑不是在类内还是在类外的问题;它用于定义现象是集合(或类)的成员的可能性有多大。模糊逻辑以集合论为基础;因此,您将定义可能性,而不是概率。
例如,在房屋适宜性模型中,如果坡度是输入条件之一,根据坡度值成为适合建筑物(或类)的适宜性集合的成员的可能性,将每个坡度值变换或指定一个介于 0 和 1 之间的值。值 1 表示完全确定值在集合中,0 表示完全确定值不在集合中。其他所有值表示某种可能性等级,较高的值表示较大的隶属可能性。将原始输入值变换为 0 到 1 的隶属可能性范围的过程称为模糊化过程。模型的每个条件(例如坡向、到公路的距离和土地利用类型)都将被模糊化。模糊分类工具用来将数据变换为 0 到 1 的可能性范围。
要确定最符合所有条件的位置(即在所有集合中具有高隶属可能性),将使用模糊叠加工具。当合并多个条件时,模糊叠加工具会确定像元隶属于由多个条件所定义的每个集合的可能性。例如,某一特定位置属于坡度、坡向和到公路的距离的良好适宜性的可能性是什么?
因此,模糊逻辑中的两个主要步骤是模糊化(或模糊分类过程)和模糊叠加分析。在一般的叠加过程中,这两个步骤分别与重分类/变换步骤和添加/合并步骤相关。
很多时候,某事物是否属于某一类是不明确的,而是主观性的。在人类语言中,这些不精确性通过修饰词进行量化,例如非常、略微和适中。模糊逻辑执行叠加分析更类似于自然的人类思维。事物不明确;边界可以是模糊的。模糊逻辑不是分析数据中的不确定性,而是探究类边界中的不精确性。
以下部分将介绍与数据分类、模糊分类过程以及执行模糊叠加分析相关的问题。还将介绍模糊逻辑与二进制及加权叠加分析方法的比较,以及模糊逻辑如何整合到一般的叠加过程中。
数据分类和模糊逻辑
要对现象进行描述或排序,一般会将它们划分为各个类。土地利用类别、土壤类型、适宜性权重、道路类和植被类型均是类的示例。在明确集合中,隶属度是二进制的,现象或者在类中,或者不在类中。类边界是清晰的。但由于想法的不精确性、分类规则的不明确性、模糊性以及矛盾心理,类之间的边界不总是明确的。
例如,如果正在探究的现象是某个组中人的不同身高的关系,您可能会根据身高先将不同的人集中到各个类中。您可能从三个类入手 - 矮个、中等和高个。需要设置各个类的边界。例如,矮个的人可能是指 5 英尺(1.524 米)及其以下的任何人,高个的人可能是指 6 英尺(1.8288 米)及其以上的任何人,中等身高的人则介于 5 英尺和 6 英尺(1.6764 和 1.8288 米)之间。身高为 6 英尺(1.8288 米)的人将位于高个类中。身高为 5' 11"(1.8034 米)的人将被划分为中等身高类。两个人的身高之间仅 1 英寸(0.0254 米)之差,却位于两个不同的类中。如果另一个组成员身高为 5' 1"(1.5494 米),第二个成员身高为 6' 6"(1.9812 米),则会表现与上面相同的差异关系。由于分类的粗糙性,无法获得各个身高之间完整的关系。
要更准确地表示不同人之间的身高关系,可添加更多的类。例如,可再添加两个类,这样矮个将为 4' 10"(1.4732 米)及其以下,中低个将为 4' 10"(1.4732 米)至 5' 4"(1.6256 米),中等身高将为 5' 4"(1.6256 米)至 5' 10"(1.778 米),中高个将为 5' 10"(1.778 米)至 6' 4"(1.9304 米),高个将为大于 6' 4"(1.9304 米)。通过类中的这种细化,可更准确地获得人的身高之间的关系。
为进一步细化,甚至可添加更多的类。无论添加了多少类,仍然存在人之间身高关系的概括。存在一些不能被划分到严格定义的类中的现象。有时,很难将现实世界分组为离散的类。
由此看来,定义类边界可以是主观的且可随现象的定义而更改。在上述定义的身高类中,假设人为成年人,很可能是男性和女性的混合形式。如果组完全由女性组成,则可能需要更改类定义。如果组由儿童组成或包含儿童,则可能需要更进一步地更改类边界。
现象的类和特征的定义描述了如何表示要建模的现象。测量误差进一步复合了分类问题。如果测量人身高的步骤的精度为正负 1 英寸(0.0254 米),则误差可更改现象被指定的类。
模糊逻辑会在分类过程中对这种不精确性进行建模。在模糊逻辑中,类被定义为集合。了解集合中成员的理想值是什么,例如,房屋适宜性模型中理想的坡度值。当值远离理想值时,明确等级会减小到某个特定点,在该点处可以明确值不是集合的成员(例如,的确过陡而无法在其上构建)。
例如,在上述身高应用中,如果从三个类(矮个、中等和高个)入手,则模糊逻辑中这三个类可以重叠。
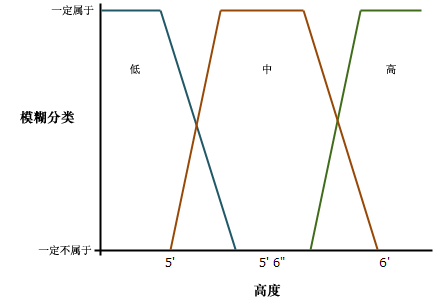
在上图中,每个类的完整隶属度为
- 矮个:< 5 英尺(1.524 米)
- 中等:5' 3 1/2"(1.6129 米)至 5' 8 1/2"(1.7399 米)
- 高个:>6(1.8288 米)
对于矮个集合(或类),身高为 5 英尺(1.524 米)及其以下的任何人确定在小个集合内并指定为 1。身高大于 5 英尺(1.524 米)且小于 5' 3 1/2"(1.6129 米)的任何人介于小个和中等集合(或类)之间。对于介于 5 英尺(1.524 米)和 5' 1 3/4"(1.6193 米)之间的身高,很可能在矮个集合中。大于 5' 1 3/4"(1.6193 米)且小于或等于 5' 3 1/2"(1.6129 米)的身高可能在矮个集合中,但更有可能是中等集合的一部分。
通常使用模糊分类工具通过预先确定的函数执行模糊化过程。
模糊分类
模糊化过程针对没有明确定义的边界的现象表征类的不精确性。
模糊化会将现象的原始值转换为属于某个定义集合的可能性。定义的集合可由适宜的、在适合的距离范围内或具有查找特定矿物的可能性组成。现象的原始值在此连续统一体上通过预定义的模糊隶属度函数或通过其他任意分类方法进行了重分类。
在模糊化过程中,对集合定义了隶属度的理想定义。更接近集合定义中心的每个现象的值将被指定为 1。确定不属于集合的值被指定为 0。落在两个极值之间的那些值位于集合的过渡区(即边界)中。当值远离理想值或集合的中心时,将被指定为从 1 到 0 的连续范围中减少的值。指定的值减少时,原始现象值成为该集合成员的可能性较小。
模糊化值 0.5 是交叉点。大于 0.5 的任意模糊值表示原始现象值可能是集合的成员。当模糊化值下降到 0.5 以下时,原始现象值是集合成员的可能性较小;值可能不是集合的一部分。
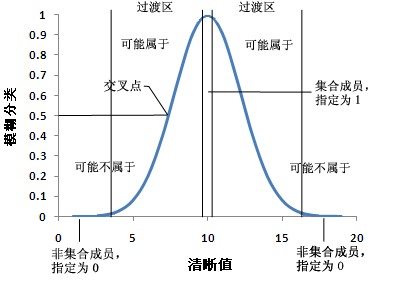
过渡区的宽度取决于要建模的现象、对现象的了解、集合的定义,以及测量的精度。更改模糊化函数的参数可定义过渡区的特征。在下图中,通过根据更改函数的参数获得的三个不同的曲线显示了模糊高斯函数。
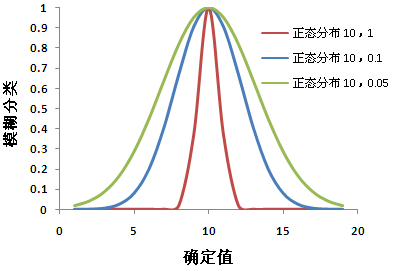
参数充当用于定义集合的修饰符。修饰符表征集合之间的潜在重叠或中间的范围。
对于叠加分析中的每个条件都会发生模糊化过程。
模糊叠加方法
要针对叠加模型中的多个条件分析所有集合之间的关系和交互,可使用模糊叠加方法。由于模糊化过程是基于集合的隶属度,所以叠加方法描述的是集合的分类中不精确性的交互。模糊叠加方法以集合论为基础。集合论在数学领域中是指将现象的成员关系量化到具体的集合。在模糊叠加分析中,集合通常与类对应。
可用的模糊集合叠加方法有 Fuzzy And、Fuzzy Or、Fuzzy Product、Fuzzy Sum 以及 Fuzzy Gamma。每种方法都描述像元与输入集合的成员关系。例如,Fuzzy And 叠加类型会创建一个输出栅格,其中为像元位置所属的每个集合的每个像元值给定了最低指定的模糊值。如果叠加分析是房屋适宜性模型且多个条件中的每个条件都已相对于其属于合适集合的隶属度被模糊化,Fuzzy And 会识别多个条件内像元属于一个合适集合的最低可能性。
Fuzzy Or 类型会返回集合交集的最大值。也就是说,在房屋适宜性模型中将针对多个条件计算每个像元的最高可能隶属度(最高适宜性值)。
二进制、加权及模糊逻辑叠加
在很多用于叠加分析的模糊逻辑介绍中,通常会将其与二进制叠加分析相比较。在二进制叠加分析中,对于每个条件,会计算每个像元是否在指定的类中。如上所述,很多情况下很难定义明确的类边界并确切地将像元指定为特定的类。在二进制分析中,对于房屋适宜性模型的示例,将针对每个条件指定每个像元为适宜 (1) 或不适宜 (0)。在叠加过程中,针对所有输入条件指定为 1 的位置被视为是可能适宜的位置。
二进制叠加分析方法的局限性包括:
- 如果没有任何满足所有条件的位置,则不会确定第二个最佳选项。
- 不存在满足条件的位置的相对权重。
- 上述关于分类过程的问题。
加权叠加分析尝试解决这些局限性。加权叠加工具会在定义的连续范围(如 1 至 10 的范围,其中 10 是相对于条件的最首选)上指定每个像元值,而不是在 1 或 0 二进制范围上对每个像元进行分类。连续的范围提供了更多类级别,从而允许进一步细化现象的表达。对于每个条件,每个像元都会被指定为 1 至 10 的范围。随后将一起添加各个重分类的条件。具有最高总和值的像元位置是相对于输入条件的最首选。每个输入适合的条件越多越好。
与二进制叠加相比,模糊叠加和加权叠加彼此更相似;然而,两者建立在不同的基础上。模糊叠加以集合论为基础,而加权叠加以线性组合为基础。两种方法均会变换原始值。在模糊叠加中,变换用于定义集合隶属的可能性,而加权叠加位于相对优先范围中。由于这两种方法是唯一的,用于在多个条件之间执行分析的工具不可互换。
模糊逻辑及常规的叠加分析过程
模糊逻辑叠加分析遵循常规的叠加分析步骤,但更多重点在于某些步骤,其他步骤则关注较少,并且相对于其他叠加分析方法指定的数字的值的含义不同。
常规的叠加分析步骤如下:
- 定义问题。
- 将问题分解为子模型。
- 确定重要图层。
- 在图层内重分类或变换数据。
- 确定输入图层的权重。
- 添加或组合图层。
- 分析。
与所有叠加分析一样,步骤 1 到步骤 3 对于模糊逻辑分析来说是相同的。由于模糊逻辑以集合为基础,重分类值(步骤 4)的含义以及可用于合并多个条件(步骤 6)的分析方法使模糊逻辑相对于其他叠加分析方法唯一。
下面的部分将介绍步骤 4 到 7 中的模糊逻辑有何不同。
在图层内重分类或变换数据
输入数据被重分类或变换为 0 到 1 范围内,从而确定属于特定集合的可能性。此重分类或模糊化过程通过模糊分类工具实现。已开发了一系列分类函数,以在变换过程中起到辅助作用。可用的函数为模糊高斯、模糊较大值、模糊线性、模糊 MS 大值、模糊 MS 小值、模糊邻近值和模糊较小值。每个分类函数都会以特定的方式变换数据,以获得现象的相互作用。
确定输入图层的权重
由于模糊逻辑以集合论为基础,并且您要确定某一特定位置是属于一个集合还是多个集合,则确定权重没有意义。将一个因素的权重增加并超过另一个因素的权重不会增加属于一个集合或多个集合的组合的可能性。位置或者是集合的成员,或者不是(连同两者之间的所有度数)。在模糊叠加分析中,确定条件的权重不适用。
添加或组合图层
在添加或组合步骤中,模糊逻辑会探究属于多个集合的现象的可能性交互,与加权叠加和加权总和相反,后两者认为适合的元素越多结果越好。
对于模糊叠加,存在特定的方法来研究这种相对关系以及用于量化交互。组合方法有 Fuzzy And、Fuzzy Or、Fuzzy Product、Fuzzy Sum 以及 Fuzzy Gamma。每种方法都以集合论为基础且特定于模糊叠加分析。
分析
与任意叠加分析一样,由您自己决定分析并解释结果。然而,由于重分类值的不同含义以及与每个叠加方法相关的叠加技术的不同,可能需要应用不同的机制来度量结果的有效性。