需要 Spatial Analyst 许可。
核密度分析工具用于计算要素在其周围邻域中的密度。此工具既可计算点要素的密度,也可计算线要素的密度。
核密度分析可用于测量建筑密度、获取犯罪情况报告,以及发现对城镇或野生动物栖息地造成影响的道路或公共设施管线。可使用 population 字段根据要素的重要程度赋予某些要素比其他要素更大的权重,该字段还允许使用一个点表示多个观察对象。例如,一个地址可以表示一栋六单元的公寓,或者在确定总体犯罪率时可赋予某些罪行比其他罪行更大的权重。对于线要素,分车道高速公路可能比狭窄的土路产生更大的影响,高压线要比标准电线杆产生更大的影响。
默认搜索半径(带宽)算法
在 ArcGIS 10.2.1 中,计算默认搜索半径的方法已得到了改善。
用于确定默认搜索半径(同时也被称为带宽)的算法如下所示:
- 计算输入点的平均中心。如果所选的 Population 字段使用的值不是 None,则此计算以下所有计算都将通过该字段中的值进行加权。
- 计算与所有点的(加权)平均中心之间的距离。
- 计算这些距离的(加权)中值 Dm。
- 计算(加权)标准距离 SD。
有关此内容的详细信息,请参阅标准距离工具。
- 使用以下公式计算带宽:
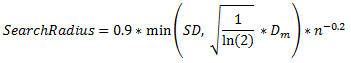
其中:
- SD 是标准距离
- Dm 是中值距离
- 如果未使用 population 字段,则 n 是点数;反之,n 则是 population 字段值的总和
这种计算默认半径的方法通常会避免出现“点周围的圆环”现象,该现象通常会随稀疏数据集而产生。
重新创建来自 ArcGIS 先前版本的结果
在 ArcGIS 10.2.1 之前的版本中,将输入范围的宽度和高度间的较小值除以 30 得出默认搜索半径。如果要再现这些结果,将输出像元大小参数的默认值乘以 25/3 或 8.333333 即可。
点要素的核密度分析
核密度分析用于计算每个输出栅格像元周围的点要素的密度。
概念上,每个点上方均覆盖着一个平滑曲面。在点所在位置处表面值最高,随着与点的距离的增大表面值逐渐减小,在与点的距离等于搜索半径的位置处表面值为零。仅允许使用圆形邻域。曲面与下方的平面所围成的空间的体积等于此点的 Population 字段值,如果将此字段值指定为 NONE 则体积为 1。每个输出栅格像元的密度均为叠加在栅格像元中心的所有核表面的值之和。核函数以 Silverman 的著作(1986 年版,第 76 页,equation 4.5)中描述的四次核函数为基础。
如果 population 字段设置使用的是除 NONE 之外的值,则每项的值用于确定点被计数的次数。例如,值 3 会导致点被算作三个点。值可以为整型也可以为浮点型。
默认情况下,单位是根据输入点要素数据的投影定义的线性单位进行选择的,或是在输出坐标系环境设置中以其他方式指定的。如果选择的是面积单位,则计算所得的像元密度将乘以相应因子,然后写入到输出栅格。
例如,如果输入单位为米,则输出面积单位将默认为平方千米。将以米和千米为单位的单位比例因子进行比较,将得到相差 1,000,000(1,000 米 x 1,000 米)倍的值。
线要素的核密度分析
核密度分析还可用于计算每个输出栅格像元的邻域内的线状要素的密度。
概念上,每条线上方均覆盖着一个平滑曲面。其值在线所在位置处最大,随着与线的距离的增大此值逐渐减小,在与线的距离等于指定的搜索半径的位置处此值为零。由于定义了曲面,因此曲面与下方的平面所围成的空间的体积等于线长度与 Population 字段值的乘积。每个输出栅格像元的密度均为叠加在栅格像元中心的所有核表面的值之和。用于线的核函数是根据 Silverman 著作中所述的用于计算点密度的四次核函数改编的。
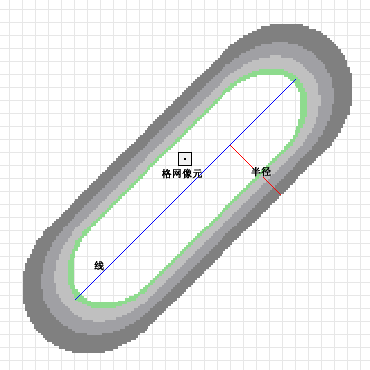
上图显示的是一条线段与覆盖在其上方的核表面。线段对密度的影响等同于栅格像元中心处核表面的值对密度的影响。
默认情况下,单位是根据输入折线要素数据的投影定义的线性单位进行选择的,或是在输出坐标系环境设置中以其他方式指定的。
指定输出面积单位因子后,它会转换长度单位和面积单位。例如,如果线性单位是米,则输出面积单位将默认为 SQUARE_KILOMETERS ,而所得到的线密度单位将转换为千米/平方千米。将以米和千米为单位的面积比例因子相比较,最终结果将是相差 1,000 倍的密度值。
您可以通过手动选择相应的因子来控制密度单位。要将密度单位设置为米/平方米(而不是默认的千米/平方千米),请将面积单位设置为 SQUARE_METERS。同样,若要将输出的密度单位设置为英里/平方英里,请将面积单位设置为 SQUARE_MILES。
有关特定距离单位的详细信息,请参阅以下主题。
如果 population 字段使用的是除 NONE 之外的值,则线的长度将由线的实际长度乘以此线的 population 字段的值而得出。
参考资料
Silverman, B. W. Density Estimation for Statistics and Data Analysis.New York:Chapman and Hall, 1986.