需要 Geostatistical Analyst 许可。
在生成最终表面之前,应该了解模型对未知位置的值所做预测的准确程度。交叉验证和验证有助于准确判断可以提供最佳预测的模型。这些计算的统计数据可用作指示模型及其相关参数值是否合理的诊断信息。
交叉验证和验证使用以下方法 – 移除一个或多个数据位置,然后使用其他位置的数据来预测与其相关联的数据。这样,您可将预测值与实测值相比较并且获得关于克里金模型质量的有用信息(例如,半变异函数参数和搜索邻域)。
交叉验证
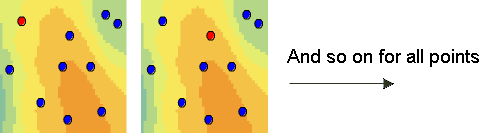
交叉验证使用所有数据对趋势和自相关模型进行估计。它会每次移除一个数据位置,然后预测关联的数据值。例如,下图显示了 10 个数据点。交叉验证会省略一个点(红色点),然后使用剩余的 9 个点(蓝色点)计算此位置的值。将省略点位置的预测值与实际值相比较。然后对第二个点重复此过程,以此类推。交叉验证会对所有点的测量值和预测值进行比较。在某种意义上,通过使用所有数据估计趋势和自相关模型,交叉验证有点欺骗性。完成交叉验证后,如果某些数据位置中含有较大误差,则这些位置可能被作为异常搁置,这时需要重新拟合趋势模型和自相关模型。
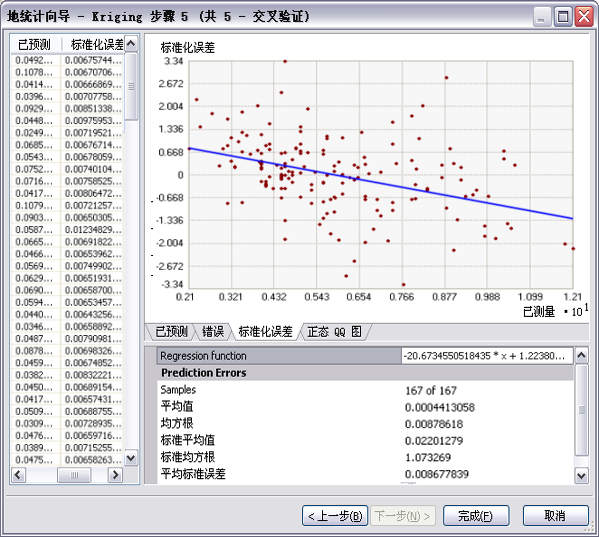
交叉验证自动执行,并且在地统计向导的最后一步中显示结果。也可以通过交叉验证地理处理工具手动执行交叉验证。
验证
验证首先会移除部分数据(称为测试数据集)。然后使用其他数据(称为训练数据集)来开发要用于预测的趋势和自相关模型。在 Geostatistical Analyst 中,使用子集要素工具创建测试数据集和训练数据集。除上述差异外,验证和交叉验证中用于比较预测和真实值的图形类型和汇总统计类型都是相似的。验证创建的模型仅针对数据的子集,因此不能直接检查包含所有可用数据的最终模型。验证检查决策“协议”是否有效,例如,半变异函数模型的选择、步长大小的选择、搜索邻域的选择。如果决策协议适用于验证,则该协议也同样适用于整个数据集。
图
Geostatistical Analyst 在“地统计向导”的最后一页提供了几个测量值和预测值的图表和汇总。给出了预测值与真实值的散点图。您可能预期这些点应该散布在 1:1 线(下图中灰色线)的附近。但是,斜率通常小于 1。克里金法的特点是往往大值的预测值过低,而小值的预测值过高,具体如下图所示:
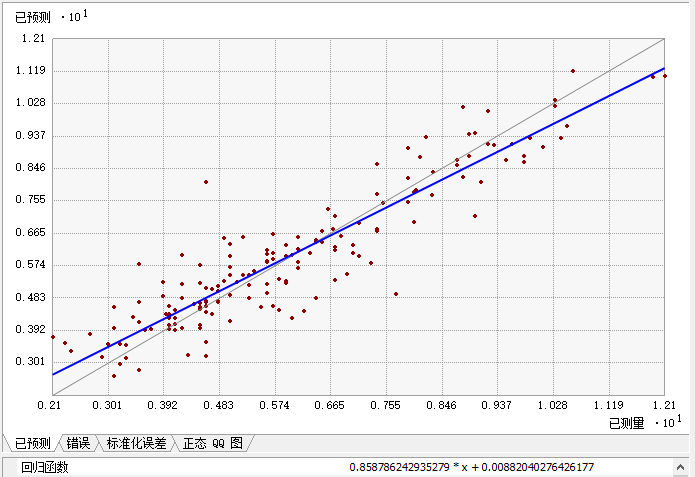
穿过分散点的拟合线显示为蓝色,并在图的下方给出方程。误差图与预测图相同,只是在预测值基础上减去了测量值。对于标准化误差图,要先用预测值减去测量值,然后再除以估计的克里金标准误差。所有三个图都显示了克里金法预测的准确程度。如果所有数据都是独立的(无自相关性),则所有预测值均相同(每一个预测值都是测量数据的平均值),因此蓝线为水平线。 如果拥有自相关性且使用的是理想的克里金模型,则蓝线应更接近于 1:1 灰色线。将使用稳健回归方程计算这三个图中每一个图下方的回归方程。此过程首先将标准线性方程的线与散点图拟合。接下来,移除回归线上方或下方超过两个标准差的所有点,并计算新的回归方程。此过程将确保不让少量异常值破坏整个回归方程。
最后一个图是 QQ 图。该图显示预测值和测量值的差值的分位数以及标准正态分布中对应的分位数。如果预测值与真实值之间的误差为正态分布,则这些点应大致沿灰色线分布。如果误差呈正态分布,则可放心使用依赖正态性的方法(例如,简单克里金法中的分位数图)。
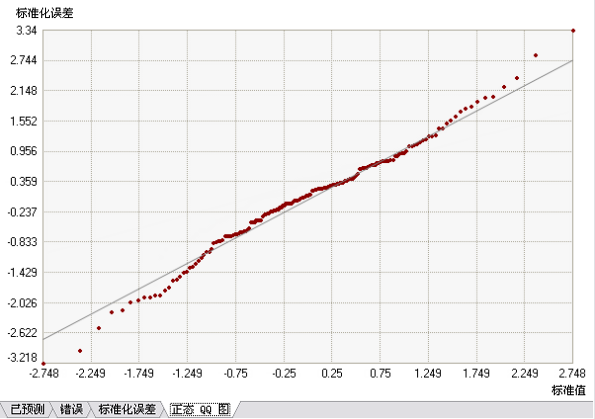
预测误差统计
最后,在下面给出了克里金预测误差的一些汇总统计数据。这些数据可用作诊断信息。这些诊断可通过交叉验证工具或地统计向导进行计算。
- 一般希望预测具有无偏性(居于真实值的中心位置)。如果预测误差具有无偏性,则平均值预测误差应接近于 0。但是,该值取决于数据的规模;要使其标准化,用预测误差除以其预测标准误差则可得到标准化的预测误差。计算后这些数值的平均值也应接近于零。
- 一般希望不确定性评估(预测标准误差)有效。每种克里金方法都提供估计的预测克里金标准误差。除执行预测之外,还会估计预测在真实值基础上的变异性。获得正确的变异性是至关重要的。例如,在普通、简单、通用和经验贝叶斯克里金法中(假设数据为正态分布),分位数图和概率图对克里金标准误差的依赖程度与对预测本身的依赖程度相同。如果平均标准误差与均方根预测误差接近,则说明正确地估计了预测中的变异性。如果平均标准误差大于均方根预测误差,则说明对预测中的变异性估计过高。如果平均标准误差小于均方根预测误差,则说明对预测中的变异性估计过低。查看此变异性的另一种方式就是用每个预测误差除以其估计的预测标准误差。平均来看它们应具有相似性,因此在预测标准误差有效时,均方根标准化误差应接近于 1。如果均方根标准化误差大于 1,则说明对预测中的变异性估计过低;如果均方根标准化误差小于 1,则说明对预测中的变异性估计过高。