该局部异常值分析工具可确定数据中的显著聚类和异常值。此工具可查找到研究区域内空间与时间上均与其邻域存在统计差异的位置。其将使用通过聚合点创建时空立方体工具创建的时空 NetCDF 立方体作为输入。然后,此工具将使用领域距离和邻域时间步长参数值计算各条柱的 Anselin Local Moran's I 统计(聚类和异常值分析)时空实现。要执行此操作,该工具需要计算出 Local Moran's I 指数、伪 P 值和类型编码 (CO_TYPE),此类型编码用于表示输入时空立方体中各统计显著性条柱的聚类或异常值类别类型。伪 p 值表示计算出的指数值的统计显著性,其精度取决于排列的数量。
可能的应用
局部异常值工具可应用至诸多领域,其中包括经济学、资源管理、政治地理学、人口统计、公共卫生和诈骗预防。您可以通过使用此工具回答下列问题:
- 我的研究区域中是否存在具有异常消费模式的位置?
- 该研究区域内是否曾经历过疾病爆发率异常高的时期?
- 是否存在居民用水量明显高于其邻域的城郊区域? 或者查找用水量始终较少的城郊区域,以便制定节约用水的最佳实践。
- 我的区域内是否存在上个月保险索赔申请数量显著增多的位置?
工具输出
此工具可创建许多输出。最杰出的输出为二维地图,它可汇总完成此工具以来添加到地图上的各个位置。类别如下:
| 类型名称 | 定义 |
|---|---|
Never Significant | 从未具有统计显著性 CO_TYPE 的位置。 |
Only High-High Cluster | 统计显著性类型始终仅为高-高聚类的位置。 |
Only High-Low Outlier | 统计显著性类型始终仅为高-低聚类的位置。 |
Only Low-High Outlier | 统计显著性类型始终仅为低-高聚类的位置。 |
Only Low-Low Cluster | 统计显著性类型始终仅为低-低聚类的位置。 |
Multiple Types | 曾经为多种统计显著性聚类类型和异常值类型的位置(例如,位置在某些时间段为低-高异常值,而在其他时间段为高-高聚类)。 |
汇总了各位置上聚类和异常值类型的二维地图,可提供杰出的输出并在工具完成后被添加到地图。此外,会将汇总了分析结果的消息写入到结果窗口中。右键单击结果窗口中的消息条目并选择查看,将在消息对话框中显示结果。
这些消息包括有关输入时空立方体的信息,例如时间跨度、时间偏差以及所分析的条柱和位置的数量。还包括有关最近时间步长内出现的所有异常值的重要信息,并汇总了可能感兴趣的关键时间步长。例如,如果您的问题是查找所在销售领域内业绩欠佳的区域,而且您正在查找高-低异常值,则消息将为您提供低-高异常值数量最多的关键时间步长。

该工具可创建出一个新输出要素类,需利用以下字段汇总输入时空立方体各位置处的条柱:
| 别名 | 字段名 |
|---|---|
| 异常值数 | NUM_OUT |
| 异常值百分比 | PERC_OUT |
| 低聚类数 | N_LOW_CLS |
| 低聚类百分比 | P_LOW_CLS |
| 低异常值数 | N_LOW_OUT |
| 低异常值百分比 | P_LOW_OUT |
| 高聚类数 | N_HIGH_CLS |
| 高聚类百分比 | P_HIGH_CLS |
| 高异常值数 | N_HIGH_OUT |
| 高异常值百分比 | P_HIGH_OUT |
仅可依赖时态邻域进行分析计算的无空间领域位置 | NO_SP_NBR |
最近时间步长内出现异常值的位置 | OUT_R_TIME |
| 聚类异常值类型 | CO_TYPE |
其他汇总统计包括所分析变量的总和、最小值、最大值、平均值、标准差和中值。 | SUM_VALUE、MIN_VALUE、MAX_VALUE、MEAN_VALUE、STD_VALUE 和 MED_VALUE |
最后,局部异常值分析工具将一些新的变量添加至输入时空立方体。如果这些变量已经存在(如果针对同一分析变量多次运行局部异常值分析工具),则会覆盖现有变量以使立方体始终包含最新的分析结果。
You may visualize these variables using ArcGIS Pro. 有关策略,请参阅可视化时空立方体。
解释
为帮助理解局部异常值分析工具的结果,可使用在 3D 模式下显示时空立方体工具显示已添加到立方体中的结果变量。通过选择 Cluster and outlier results 显示主题,可显示各条柱的指数、p 值和聚类异常值分析类型。指数具有正值时表示条柱具有包含同样高或同样低的属性值的相邻条柱;该条柱是聚类的一部分。指数具有负值时表示条柱具有包含不同值的邻近条柱;该条柱是异常值。在这两个实例中,要素的伪 p 值或 p 值必须足够小,才能认为聚类或异常值具有统计显著性。有关确定统计显著性的详细信息,请参阅什么是 z 得分? 什么是 p 值?。请注意,Local Moran's I 指数 (I) 是相对测量,只能在其生成的参考分布和计算出的伪 p 值或 p 值环境中进行说明。在输出要素类中报告的伪 p 值和 p 值对于多重测试和空间依赖性来说已经校正。
聚类或异常值类型可区分具有统计显著性的高值(高-高)聚类、低值(低-低)聚类、高值主要由低值围绕的异常值(高-低)以及低值主要由高值围绕的异常值(低-高)。统计显著性的置信度设置为 95%。此显著性表示 FDR 校正,即将此 p 值阈值从 0.05 调整为某个新值,以便在兼顾多重测试的情况下更好地反映置信度 95%。
邻域默认值
要确定处于空间和时间中某位置的条柱值是否是具有统计显著性的热点或冷点或者是否为统计显著性异常值的一部分,可在每个条柱的相邻时空条柱范围内对其进行评估。邻域距离和邻域时间步长的参数值可定义每个条柱邻域的范围(每个条柱分析的上下文)。假设条柱维度为 400 米乘 400 米乘 1 天。如果将邻域距离设置为 801 米,将邻域时间步长设置为 2,则空间邻域将在水平和垂直两个方向延长两个条柱,并且对角延伸一个条柱,如下所示: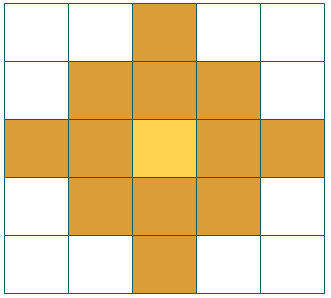
此外,还有时间邻域。作为目标的同一位置上的所有条柱,以及匹配的时间段或两个先前时间段(对于本例一共为三天)的空间邻域(如上图所示)将被作为邻域包括在内。请注意,时间邻域仅后向聚合时间;值为 2 的邻域时间步长包含三个时间步长间隔。为确保每个位置至少有 1 个时间邻域,在第一个时间片中不会计算条柱的 Local Moran's 指数。但是,第一个时间片中的条柱值将包含在全局平均值的计算中。
如果未提供邻域距离参数值,则会为您计算一个值。公式改编自用于确定默认核密度搜索半径的计算。如果未提供邻域时间步长的值,则默认值设置为 1。
排列
排列用于确定找到您所分析值的实际空间分布的可能性,方法是将您的值与一组随机生成的值进行比较。即便存在完全空间随机性 (CSR),而一定程度的聚类仍可仅通过随机性进行观察。排列将会生成许多随机性数据集,并将这些值与原始数据的 Local Moran's I 进行比较。要执行此操作,每个排列均会随机重新排列各条柱周围的邻域值,并计算该随机数据的 Local Moran's I 值。通过查看排列所生成的 Local Moran's I 分布,您即可获悉由随机性决定的 Local Moran's I 值的范围。如果数据中存在统计显著性空间模式,您预期从排列中生成的 Local Moran's I 值比原始数据中生成的 Local Moran's I 值所显示的聚类更少。随后,可以通过确定排列中生成的 Local Moran's I 值(其中显示的聚类较原始数据多)的比例计算出伪 p 值。如果该比例(伪 p 值)很小(小于 0.05),则可以推断出您的数据确实具有统计显著性聚类。
选择排列数时需要兼顾精度和所需增加的处理时间。增加排列数将凭借扩大伪 p 值的可能值范围而提高精度。例如,采用 99 次排列时,伪 p 值精度为 .01 (1/99+1),而采用 999 次排列时,精度则为 .001 (1/999+1)。最初研究问题时可以使用较少的排列数,但是要使最终结果的可行性达到最高,则增加排列数不失为最佳实践。
其他资源
Anselin, Luc. Local Indicators of Spatial Association—LISA, Geographical Analysis 27(2): 93–115, 1995.
Mitchell, Andy. The ESRI Guide to GIS Analysis, Volume 2. ESRI Press, 2005.