需要 Spatial Analyst 许可。
需要 3D Analyst 许可。
山体阴影工具通过为栅格中的每个像元确定照明度,来获取表面的假定照明度。通过设置假定光源的位置和计算与相邻像元相关的每个像元的照明度值,即可得出假定照明度。进行分析或图形显示时,特别是使用透明度时,“山体阴影”工具可大大增强表面的可视化。
默认情况下,阴影和光线是与介于 0 和 255 之间的整数相关的灰度梯度(从黑色渐变为白色)。
山体阴影参数
在为任何特定位置创建山体阴影地图时,所要考虑的主要因素是太阳在天空中的位置。
方位角
方位角指太阳的角度方向,是以北为基准方向,在 0 到 360 度范围内按顺时针进行测量的。90 度的方位角指向为东。默认方位角为 315 度 (NW)。

高度角
高度角指的是照明源高出地平线的角度或坡度。高度角的单位为度,范围为 0(位于地平线上)到 90(位于头上)之间。默认值为 45 度。
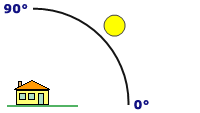
下面的山体阴影示例的方位角为 315 度,高度角为 45 度。

使用山体阴影进行显示
通过将高程栅格放置在山体阴影栅格的上方,然后对高程栅格的透明度进行调整,可轻松创建外观精美的地表地貌图。

您可以添加其他图层(如土地使用类型、植被、道路或河流),从而进一步丰富显示中的信息内容。
在分析中使用山体阴影
通过对阴影进行建模(默认选项),可计算局部照明度以及像元是否落入阴影内。
通过对阴影进行建模,可识别一天的特定时间内将要落入其他像元阴影的各个像元。位于其他像元阴影中的像元编码为 0;所有其他像元的编码为介于 1 和 255 之间的整数。可将所有大于 1 的值重分类为 1,从而生成二元输出栅格。在以下示例中,黑色区域位于阴影内。这两张图像中的方位角相同,只是太阳角度(高度角)已修改。

如何计算山体阴影
要计算阴影值,首先需要提供光照源的高度角和方向角。在计算坡度和坡向的同时会处理这些值,从而确定输出栅格中每个像元的最终山体阴影值。
山体阴影算法
用于计算山体阴影值的算法如下:
(1) Hillshade = 255.0 * ((cos(Zenith_rad) * cos(Slope_rad)) +
(sin(Zenith_rad) * sin(Slope_rad) * cos(Azimuth_rad - Aspect_rad)))请注意,如果山体阴影值的计算结果 < 0,则输出像元值将 = 0。
计算入射角度
以高于地平线的角度指定照明源的高度角。但是,用于计算山体阴影值的公式要求以弧度为单位表示角度且从垂直方向偏转角度。将垂直于表面的方向(头顶正上方)标注为天顶。天顶角为天顶点与光源方向的夹角,是高度角的余角。要计算入射角度,第一步是将高度角转换为天顶角。第二步是将天顶角转换为弧度。
将高度角转换为天顶角:
(2) Zenith_deg = 90 - Altitude转换为弧度:
(3) Zenith_rad = Zenith * pi / 180.0计算入射方向
以度为单位指定照明源的方向和方位角。山体阴影公式要求方位角采用弧度作为单位。首先,将方位角从地理单位(罗盘方向)转换为数学单位(直角)。然后,将方位角转换为弧度。
转换方位角的方法:
(4) Azimuth_math = 360.0 - Azimuth + 90请注意,如果 Azimuth_math >= 360.0,则:
(5) Azimuth_math = Azimuth_math - 360.0转换为弧度:
(6) Azimuth_rad = Azimuth_math * pi / 180.0计算坡度和坡向
移动的 3 x 3 窗口会访问输入栅格中的每个像元,窗口中心的每个像元的坡向和坡度将使用包含该像元的八个相邻像元的值的算法进行计算。这些像元使用字母 a 至 i 进行标识,其中 e 表示当前正在计算坡向的像元。
像元 e 在 x 方向上的变化率将通过以下算法进行计算:
(7) [dz/dx] = ((c + 2f + i) - (a + 2d + g)) / (8 * cellsize)像元“e”在 y 方向上的变化率使用以下算法计算:
(8) [dz/dy] = ((g + 2h + i) - (a + 2b + c)) / (8 * cellsize)坡度是从表面中的每个像元开始的最陡坡降。以下算法用于计算以弧度为单位的坡度(其中包含 z 因子):
(9) Slope_rad = ATAN (z_factor * √ ([dz/dx]2 + [dz/dy]2)) 最陡坡降的方向就是坡向的朝向。使用范围为 0 到 2pi 之间的弧度来定义坡向,其中 0 表示朝东。根据以下算法中的规则确定坡向:
(10) If [dz/dx] is non-zero:
Aspect_rad = atan2 ([dz/dy], -[dz/dx]) if Aspect_rad < 0 then Aspect_rad = 2 * pi + Aspect_rad If [dz/dx] is zero:
if [dz/dy] > 0 then Aspect_rad = pi / 2 else if [dz/dy] < 0 then Aspect_rad = 2 * pi - pi / 2 else Aspect_rad = Aspect_rad山体阴影计算示例
例如,将计算移动窗口内中心像元的山体阴影值。
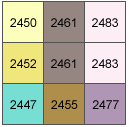
像元大小为 5 个单位。将使用 45 度的默认高度角和 315 度的默认方位角。
- 入射角度
根据等式 2 计算天顶角所得出的结果为:
(2) Zenith_deg = 90 - Altitude = 90 - 45 = 45根据等式 3 将天顶角转换为弧度的计算结果为:
(3) Zenith_rad = Zenith_deg * pi / 180.0 = 45 * 3.1428571429 / 180 = 0.7857142857 - 入射方向
使用等式 4 将天顶角从地理角度转换为数学角度的计算结果为:
(4) Azimuth_math = 360.0 - Azimuth + 90 = 360.0 - 315 + 90 = 135 = 2.3571428571使用等式 6 将天顶角转换为弧度的计算结果为:
(6) Azimuth_rad = Azimuth_math * pi / 180.0 = 135 * 3.1438571429 / 180
- 坡度和坡向
中心像元 e 在 x 方向上的变化率的计算结果为:
(7) [dz/dx] = ((c + 2f + i) - (a + 2d + g)) / (8 * cellsize) = ((2483 + 4966 + 2477) - (2450 + 4904 + 2447)) / (8 * 5) = (9926 - 9801)/ 40 = 3.125中心像元 e 在 y 方向上的变化率的计算结果为:
(8) [dz/dy] = ((g + 2h + i) - (a + 2b + c)) / (8 * cellsize) = (2447 + 4910 + 2477) - (2450 + 4922 + 2483) / (8 * 5) = (9834 - 9855) / 40 = -0.525坡度角的计算结果为:
(9) Slope_rad = ATAN ( z_factor * √ ([dz/dx]2 + [dz/dy]2)) = atan(1 * sqrt(3.125 * 3.125 + -0.525 * -0.525)) = 1.26511根据规则 10 计算 Aspect_rad 角(因为本例中 dz/dx 为非零值)所得出的结果为:
Aspect_rad = atan2 ([dz/dy], -[dz/dx]) = atan2(-0.525, -3.125) = -2.9751469600412由于此值小于 0,因此应用该规则的以下部分:
Aspect_rad = 2 * pi + Aspect_rad = 2 * 3.1428571429 + -2.9751469600412 = 3.310567 - 山体阴影
山体阴影的最终计算结果为:
H山体阴影 = 255.0 * ((cos(Zenith_rad) * cos(Slope_rad)) + (sin(Zenith_rad) * sin(Slope_rad) * cos(Azimuth_rad - Aspect_rad))) = 255.0 * ((cos(0.7857142857) * cos(1.26511)) + (sin(0.7857142857) * sin(1.26511) * cos(2.3571428571 - 3.310567))) = 153.82
因为输出栅格为整型,所以中心像元 e 的阴影值为 154。
参考资料
Burrough, P. A. and McDonell, R. A., 1998. Principles of Geographical Information Systems (Oxford University Press, New York), 190 pp.