需要 Geostatistical Analyst 许可。
由于您是在二维空间内进行操作,因此可能希望半变异函数和协方差函数不仅随距离发生改变,还会随方向发生改变。这被称为各向异性。
考虑两个点 si 和 sj,以及分开这两个点的矢量,这个矢量记为 si - sj。该矢量在 x 轴和 y 轴上都具有距离。或者,在极坐标中可将该矢量视为具有距离和角度。此处,各向异性用于描述半变异函数;思路与协方差函数类似。
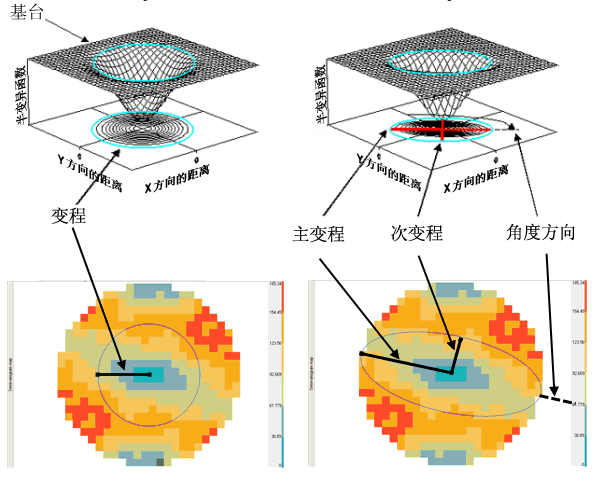
各向同性模型在所有方向上都是相同的,而各向异性模型在某些方向上达到基台的速度高于另一些方向。达到基台的较长轴的长度称为主变程,达到基台的较短轴的长度称为次变程,还具有形成主变程的线的旋转角度。在 Geostatistical Analyst 中,变程的轮廓在经验半变异函数的表面上以蓝色显示。