需要 3D Analyst 许可。
自然邻域插值可找到距查询点最近的输入样本子集,并基于区域大小按比例对这些样本应用权重来进行插值(Sibson,1981)。该插值也称为 Sibson 或“区域占用(area-stealing)”插值。该插值方法的基本属性是它具有局部性,仅使用查询点周围的样本子集,且保证插值高度在所使用的样本范围之内。该插值方法不会推断趋势且不会生成输入样本尚未表示的山峰、凹地、山脊或山谷。该表面将通过输入样本且在除输入样本位置之外的其他所有位置均是平滑的。如果采用“TIN 转栅格”的插值方式,可使用断裂线增大表面,以在适当的位置(例如沿路边和水体)创建线性不连续的地形。该插值方法根据输入数据的结构进行局部调整,而无需来自用户的与搜索半径、样本计数或形状有关的输入。对于规则和不规则分布的数据,它的效果一样好(Watson,1992)。
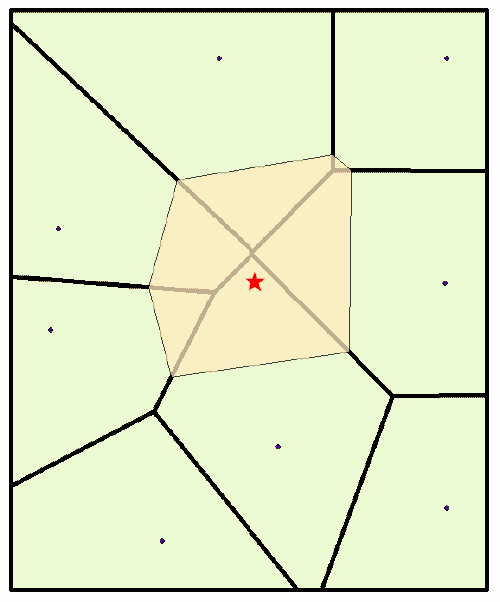
所有点的自然邻域都与邻近 Voronoi(泰森)多边形相关。最初,Voronoi 图由所有指定点构造而成,并由橄榄色的多边形表示。然后会在插值点(红星)周围创建米色的新 Voronoi 多边形。这个新的多边形与原始多边形之间的重叠比例将用作权重。
相比之下,基于距离的插值器(如反距离加权 (IDW))会根据距插值点相同的距离为最北部的点和最南部的点分配相同权重。但是,自然邻域插值会根据重叠百分比将权重分别指定为 19.12% 和 0.38%。
参考书目
Sibson, R. 所著《多元数据插值》(Interpolating Multivariate Data) 第 21–36 页第二章“自然邻域插值简介”。John Wiley & Sons:纽约,1981 年版。
Watson, D. 所著《等高线绘制:空间数据分析和显示指导》(Contouring:A Guide to the Analysis and Display of Spatial Data)。Pergamon Press:伦敦,1992 年版。