ArcMap

波段集统计的工作原理

需要 Spatial Analyst 许可。

波段集统计工具用于为栅格波段集的多元分析提供统计值。启用计算协方差和相关矩阵选项时，协方差和相关矩阵与基本统计参数（如每个图层的最小值、最大值、平均值和标准差）会一同输出。

协方差矩阵包含方差值和协方差值。方差是表明与平均值之间的差异的统计测量值。对各像元值与所有像元的平均值的差取平方，然后求取这些平方值的平均值，即可求得方差。可沿协方差矩阵的对角线从左上角至右下角读取每个图层的方差值。方差的单位为像元值单位的平方。

协方差矩阵中的剩余元为所有输入栅格对之间的协方差。以下公式可用于确定图层 i 与图层 j 之间的协方差：

计算图层 i 与图层 j 之间协方差的公式

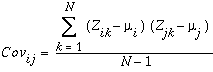
  • 其中：

    Z - 像元值

    i, j - 堆叠图层

    µ - 图层平均值

    N - 像元的数量

    k - 表示特定像元

两图层的协方差为相应行与列的交点。图层 2 与图层 3 之间的协方差与图层 3 与图层 2 之间的协方差是相同的。协方差矩阵值取决于值的单位，而相关矩阵的值则并非如此。

相关矩阵显示相关系数值，该值可描述两个数据集之间的关系。对于一组栅格图层，相关矩阵表示一个栅格图层中的像元值，而这些像元值与另一图层的像元值相关联。两图层间的相关性可用于衡量图层间依存关系。相关性为两图层间的协方差与两图层标准差乘积的比值。由于相关性是一个比值，因此不具有单位。计算相关性的公式如下：

计算相关性的公式

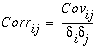
相关性的范围为 +1 至 -1。正相关性表明两图层间有直接关系，例如，当其中一个图层的像元值增大时，另一个图层的像元值也可能增大。负相关性则表示一个变量随另一个变量反比例变化。相关性为零时，表示两个图层之间不存在依存关系。

相关矩阵为对称矩阵。由于相同图层的相关系数为 +1，因此其左上角至右下角的对角线上所有值都是 1.0000。

示例

以下示例显示了四图层多波段栅格波段集统计的输出内容。第一个表显示的是未使用计算矩阵选项时的基本统计数据。然而，选中该选项时，仍会计算协方差和相关矩阵。将显示输出统计文件中所包含的输出统计值。

仅计算平均值

禁用计算协方差和相关矩阵的输出（简要）：

#               STATISTICS of INDIVIDUAL LAYERS

#   Layer           MIN          MAX          MEAN         STD
# ---------------------------------------------------------------
       1            1.0000      21.0000       7.8410       4.1690
       2            1.0000     128.0000      25.5144      35.8494
       3          296.9573    4073.6306    1565.5359     763.9803
       4            0.3333     127.5000      51.5314      29.7958
# ===============================================================

对平均值和矩阵均进行了计算

启用计算协方差和相关矩阵的输出（详细）：

#               STATISTICS of INDIVIDUAL LAYERS

#   Layer           MIN          MAX          MEAN         STD
# ---------------------------------------------------------------
       1            1.0000      21.0000       7.8410       4.1690
       2            1.0000     128.0000      25.5144      35.8494
       3          296.9573    4073.6306    1565.5359     763.9803
       4            0.3333     127.5000      51.5314      29.7958
# ===============================================================



#                    COVARIANCE MATRIX

#   Layer            1            2            3            4
# ---------------------------------------------------------------
       1           17.3826      16.9320    3177.5947      87.9590
       2           16.9320    1285.3096    3117.1753      31.3420
       3         3177.5947    3117.1753  583723.0625   16137.9785
       4           87.9590      31.3420   16137.9785     887.8751
# ===============================================================


#                    CORRELATION MATRIX

#    Layer            1            2            3            4
# ---------------------------------------------------------------
       1            1.0000       0.1133       0.9976       0.7080
       2            0.1133       1.0000       0.1138       0.0293
       3            0.9976       0.1138       1.0000       0.7089
       4            0.7080       0.0293       0.7089       1.0000
# ===============================================================

参考资料

Snedecor, G. W., and W. G. Cochran. 1968. Statistical Methods, 6th ed. Ames, Iowa:The Iowa State University Press.

相关主题