ArcMap

曲率工具的工作原理

需要 Spatial Analyst 许可。

需要 3D Analyst 许可。

曲率工具会逐个像元地计算输入表面的二阶导数值。

每个像元的四阶多项式的形式为：

 Z = Ax²y² + Bx²y + Cxy² + Dx² + Ey² + Fxy + Gx + Hy + I
适用于由一个 3x3 窗口组成的表面。系数 a、b、c 等将基于该表面计算得出。

对于示意图中显示的每个编号像元，系数和九个高程值之间的关系如下所示：

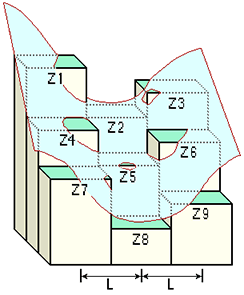
曲率值示意图
曲率值示意图
 A = [(Z1 + Z3 + Z7 + Z9) / 4  - (Z2 + Z4 + Z6 + Z8) / 2 + Z5] / L4 B = [(Z1 + Z3 - Z7 - Z9) /4 - (Z2 - Z8) /2] / L3 C = [(-Z1 + Z3 - Z7 + Z9) /4 + (Z4 - Z6)] /2] / L3 D = [(Z4 + Z6) /2 - Z5] / L2 E = [(Z2 + Z8) /2 - Z5] / L2 F = (-Z1 + Z3 + Z7 - Z9) / 4L2 G = (-Z4 + Z6) / 2L H = (Z2 - Z8) / 2L I = Z5

曲率工具的输出是该表面的二阶导数（例如，坡度的坡度），这样：

 Curvature = -2(D + E) * 100

从应用的角度看，该工具的输出可用于描述流域盆地的物理特征，从而便于理解侵蚀过程和径流形成过程。坡度会影响下坡时的总体移动速率。坡向将决定流向。剖面曲率将影响流动的加速和减速，进而将影响到侵蚀和沉积。平面曲率会影响流动的汇聚和分散。

以栅格形式显示等值线将有助于理解和诠释通过执行曲率工具得到的数据。该过程的示例如下：

诠释通过曲率工具得出的结果

以栅格形式显示等值线将有助于理解和诠释通过执行“曲率”工具得到的数据。该过程的示例如下。

  1. 创建一个曲率栅格：

    输入栅格：elev_ras

    输出曲率栅格：curv_ras

    Z 因子：1

    输出剖面曲线栅格：profile_ras

    输出平面曲线栅格：plan_ras

  2. 创建表面栅格的等值线：

    输入栅格：elev_ras

    输出折线要素：cont_lines

    等值线间距：100

    起始等值线：""

    Z 因子：1

  3. 创建坡度栅格：

    输入栅格：elev_ras

    输出栅格：slope_ras

    输出测量单位：DEGREE

    Z 因子：1

  4. 然后创建坡度的等值线：

    输入栅格：slope_ras

    输出折线要素：cont_slope

    等值线间距：5

    起始等值线：""

    Z 因子：1

  5. 将曲率栅格作为图层添加到 ArcMap 中。叠加刚刚创建的两个等值线要素数据集并为每个数据集应用不同颜色的符号系统。

参考资料

Moore, I. D., R. B. Grayson, and A. R. Landson. 1991. Digital Terrain Modelling: A Review of Hydrological, Geomorphological, and Biological Applications. Hydrological Processes 5: 3-30.

Zeverbergen, L. W., and C. R. Thorne. 1987. Quantitative Analysis of Land Surface Topography. Earth Surface Processes and Landforms 12: 47–56.

相关主题