需要 Spatial Analyst 许可。
主成分分析工具用于将输入多元属性空间中的输入波段内的数据变换到相对于原始空间对轴进行旋转的新的多元属性空间。新空间中的轴(属性)互不相关。之所以在主成分分析中对数据进行变换,主要是希望通过消除冗余的方式来压缩数据。
在包含高程、坡度和坡向(连续范围中)的多波段栅格中,数据冗余现象较为明显。由于坡度和坡向通常由高程得出,因此研究区域内的多数方差只能通过高程来解释。
此工具生成的是波段数与指定的成分数相同的多波段栅格(新多元空间中每个轴或成分一个波段)。第一个主成分将具有最大的方差,第二个主成分将具有未通过第一个主成分描述的第二大方差,依此类推。多数情况下,主成分工具生成的多波段栅格中的前三个或前四个栅格将对 95% 以上的方差进行描述。可以将其余各栅格波段删除。因为新的多波段栅格所包含的波段数较少,而且 95% 以上的原始多波段栅格方差保持不变,因此计算速度更快,同时还保持了精度。
主成分需要要标识的输入波段、要将数据变换到其中的主成分的数量、统计输出文件的名称以及输出栅格的名称。输出栅格将包含数目与指定的成分数相同的波段。一个波段描述一种成分。
主成分分析概念
从概念上讲,使用双波段栅格、轴的平移和旋转以及数据的变换都是通过以下方式完成的:
- 在散点图上绘制数据。
- 计算椭圆以限制散点图中点的范围(见下图)。
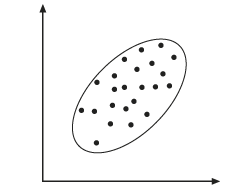
所绘制的椭圆边界 - 确定椭圆的主轴(见下图)。主轴成为新的 x 轴,即第一主成分 (PC1)。由于 PC1 是可在椭圆上绘制的最大样带,因此它可描述最大方差。PC1 的方向为特征向量,其量级为特征值。PC1 与 x 轴的夹角即是在变换中使用的旋转角度。
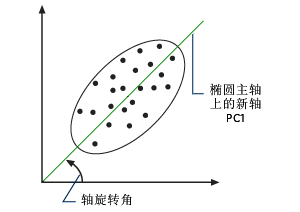
第一主成分 - 计算垂直于 PC1 的正交线。此线为第二主成分 (PC2),也是对应于原始 y 轴的新轴(见下图)。该新轴可描述未由 PC1 描述的最大方差。
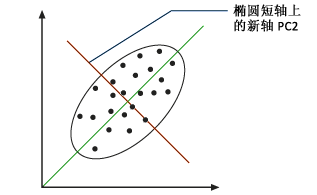
第二主成分
使用特征向量、特征值和计算出的多波段栅格输入的协方差矩阵,创建用于定义平移和旋转的线性公式。此公式可用于对各个像元值相对于新轴进行变换。
示例
以下是为三个主成分创建的输出数据文件的示例:
COVARIANCE MATRIX # Layer 1 2 3 # ----------------------------------------------------------- 1 34.1763 31.2377 51.8100 2 31.2377 212.6159 99.9540 3 51.8100 99.9540 118.8057 # =========================================================== # CORRELATION MATRIX # Layer 1 2 3 # ----------------------------------------------------------- 1 1.0000 0.3665 0.8131 2 0.3665 1.0000 0.6289 3 0.8131 0.6289 1.0000 # =========================================================== # EIGENVALUES AND EIGENVECTORS # Number of Input Layers Number of Principal Component Layers 3 3 # PC Layer 1 2 3 # ----------------------------------------------------------- # Eigen Values 287.8278 69.8781 7.8920 # Eigen Vectors # Input Layer 1 0.2112 0.4718 0.8560 2 0.8116 -0.5727 0.1154 3 0.5447 0.6704 -0.5039 # ===========================================================
参考书目
Campbell, James B. Introduction to Remote Sensing.The Guilford Press. 1987.
Jensen, John R. Introductory Digital Image Processing:A Remote Sensing Perspective.Prentice–Hall. 1986.
Lillesand, Thomas M., and Ralph W. Kiefer. Remote Sensing and Image Processing.John Wiley and Sons. 1987.
Richards, John A. Remote Sensing Digital Image Analysis:An Introduction.Berlin:Springer–Verlag. 1986.