This document provides additional information about tool parameters but also introduces essential vocabulary and concepts that are important when you analyze your data using the Spatial Statistics tools. Use this document as a reference when you need additional information about tool parameters.
Conceptualization of spatial relationships
An important difference between spatial and traditional (aspatial or nonspatial) statistics is that spatial statistics integrate space and spatial relationships directly into their mathematics. Consequently, many of the tools in the spatial statistics toolbox require the user to select a value for the Conceptualization of Spatial Relationships parameter prior to analysis. Common conceptualizations include inverse distance, travel time, fixed distance, K nearest neighbors, and contiguity. The conceptualization of spatial relationships you use will depend on what you're measuring. If you're measuring clustering of a particular species of seed-propagating plant, for example, inverse distance is probably most appropriate. However, if you are assessing the geographic distribution of a region's commuters, travel time or travel cost might be better choices for describing those spatial relationships. For some analyses, space and time might be less important than more abstract concepts such as familiarity (the more familiar something is, the more functionally near it is) or spatial interaction (there are many more phone calls, for example, between Los Angeles and New York than between New York and a smaller town nearer to New York, like Poughkeepsie; some might argue that Los Angeles and New York are functionally closer).
The Grouping Analysis tool contains a parameter called Spatial Constraints, and while the parameter options are similar to those described for the Conceptualization of Spatial Relationships parameter, they are used differently. When a spatial constraint is imposed, only features that share at least one neighbor (as defined by contiguity, nearest neighbor relationships, or triangulation methods), may belong to the same group. Additional information and examples are included in How Grouping Analysis works.
Options for the Conceptualization of Spatial Relationships parameter are discussed below. The option you select determines neighbor relationships for tools that assess each feature within the context of neighboring features. These tools include the Spatial Autocorrelation (Global Moran's I), Hot Spot Analysis (Getis-Ord Gi*), and Cluster and Outlier Analysis (Anselin Local Moran's I) tools. Note that some of these options are only available if you use the Generate Spatial Weights Matrix or Generate Network Spatial Weights tools.
Inverse distance, inverse distance squared (impedance)
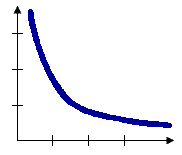
With the Inverse Distance options, the conceptual model of spatial relationships is one of impedance, or distance decay. All features impact/influence all other features, but the farther away something is, the smaller the impact it has. You will generally want to specify a Distance Band or Threshold Distance value when you use an inverse distance conceptualization to reduce the number of required computations, especially with large datasets. When no distance band or threshold distance is specified, a default threshold value is computed for you. You can force all features to be a neighbor of all other features by setting Distance Band or Threshold Distance to zero.
Inverse Euclidean distance is appropriate for modeling continuous data such as temperature variations, for example. Inverse Manhattan distance might work best when analyses involve the locations of hardware stores or other fixed urban facilities, in the case where road network data isn't available. The conceptual model when you use the Inverse Distance Squared option is the same as with Inverse Distance except the slope is sharper, so neighbor influences drop off more quickly and only a target feature's closest neighbors will exert substantial influence in computations for that feature.
Distance band (sphere of influence)

For some tools, like Hot Spot Analysis, a fixed distance band is the default conceptualization of spatial relationships. With the Fixed Distance Band option, you impose a sphere of influence, or moving window conceptual model of spatial interactions onto the data. Each feature is analyzed within the context of those neighboring features located within the distance you specify for Distance Band or Threshold Distance. Neighbors within the specified distance are weighted equally. Features outside the specified distance don't influence calculations (their weight is zero). Use the Fixed Distance Band method when you want to evaluate the statistical properties of your data at a particular (fixed) spatial scale. If you are studying commuting patterns and know that the average journey to work is 15 miles, for example, you may want to use a 15-mile fixed distance for your analysis. See Selecting a fixed distance for strategies that can help you identify an appropriate scale of analysis.
Zone of indifference
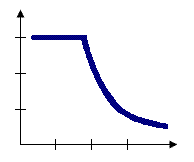
The Zone of Indifference option for the Conceptualization of Spatial Relationships parameter combines the Inverse Distance and Fixed Distance Band models. Features within the distance band or threshold distance are included in analyses for the target feature. Once the critical distance is exceeded, the level of influence (the weighting) quickly drops off. Suppose you're looking for a job and have the choice between a job five miles away and another job six miles away. You probably won't think much about distance in making a decision about which job to take. Now, suppose you have the choice between one job five miles away and another 20 miles away. In this case, distance becomes more of an impedance and may be factored into your decision making. Use this method when you want to hold the scale of analysis fixed but don't want to impose sharp boundaries on the neighboring features included in target feature computations.
Polygon contiguity (first order)
For polygon feature classes, you can choose CONTIGUITY_EDGES_ONLY (sometimes called the Rook's Case) or CONTIGUITY_EDGES_CORNERS (sometimes referred to as Queen's Case). For CONTIGUITY_EDGES_ONLY, polygons that share an edge (that have coincident boundaries) are included in computations for the target polygon. Polygons that do not share an edge are excluded from the target feature computations. For CONTIGUITY_EDGES_CORNERS, polygons that share an edge and/or a corner will be included in computations for the target polygon. If any portion of two polygons overlap, they are considered neighbors and will be included in each other's computations. Use one of these contiguity conceptualizations with polygon features in cases where you are modeling some type of contagious process or are dealing with continuous data represented as polygons.
K nearest neighbors
Neighbor relationships may also be constructed so that each feature is assessed within the spatial context of a specified number of its closest neighbors. If K (the number of neighbors) is 8, then the eight closest neighbors to the target feature will be included in computations for that feature. In locations where feature density is high, the spatial context of the analysis will be smaller. Similarly, in locations where feature density is sparse, the spatial context for the analysis will be larger. An advantage to this model of spatial relationships is that it ensures there will be some neighbors for every target feature, even when feature densities vary widely across the study area. This method is available using the Generate Spatial Weights Matrix tool. The K_NEAREST_NEIGHBORS option with 8 for Number of Neighbors is the default conceptualization used with Exploratory Regression to assess regression residuals.
Delaunay triangulation (natural neighbors)
The Delaunay Triangulation option constructs neighbors by creating Voronoi triangles from point features or from feature centroids such that each point/centroid is a triangle node. Nodes connected by a triangle edge are considered neighbors. Using Delaunay triangulation ensures every feature will have at least one neighbor even when data includes islands and/or widely varying feature densities. Do not use the Delaunay Triangulation option when you have coincident features. This method is available using the Generate Spatial Weights Matrix tool.
Space-Time window
With this option you define feature relationships in terms of both a space (fixed distance) and a time (fixed-time interval) window. This option is available when you create a spatial weights matrix file using the Generate Spatial Weights Matrix tool. When you select SPACE_TIME_WINDOW, you will also be required to specify a Date/Time Field, a Date/Time Interval Type (HOURS, DAYS, or MONTHS, for example), and a Date/Time Interval Value. The interval value is an integer. If you selected HOURS for the Interval Type and a 3 for Interval Value, for example, two features would be considered neighbors if the values in their Date/Time field were within three hours of each other. With this conceptualization, features are neighbors if they fall within the specified distance and also fall within the specified time interval of the target feature. As one possible example, you would select the SPACE_TIME_WINDOW Conceptualization of Spatial Relationships if you wanted to create a spatial weights matrix file to use with Hot Spot Analysis in order to identify space-time hot spots. Additional information, including how to visualize results, is presented in Space-Time Analysis. Other opportunities are available to help you visualize, in 3D, a netCDF space-time cube.
Get spatial weights from file (user-defined spatial relationships)
You can create a file to store feature neighbor relationships using either the Generate Spatial Weights Matrix tool or the Generate Network Spatial Weights tool. If you want to define spatial relationships using travel time or travel costs derived from a network dataset, create a spatial weights matrix file using the Generate Network Spatial Weights tool, then use the resultant SWM file for your analyses. If the spatial relationships for your features are defined in a table, use the Generate Spatial Weights Matrix tool to convert that table into a spatial weights matrix (.swm) file. Particular fields should be included in your table in order to use the CONVERT_TABLE option to obtain an SWM file. You can also provide a path to a formatted ASCII text file that defines your own custom conceptualization of spatial relationships (based on spatial interaction, for example).
Selecting a conceptualization of spatial relationships: Best practices
The more realistically you can model how features interact with each other in space, the more accurate your results will be. Your choice for the Conceptualization of Spatial Relationships parameter should reflect inherent relationships among the features you are analyzing. Sometimes your choice will also be influenced by characteristics of your data.
The inverse distance methods (INVERSE_DISTANCE, INVERSE_DISTANCE_SQUARED), for example, are most appropriate with continuous data or to model processes where the closer two features are in space, the more likely they are to interact/influence each other. With this spatial conceptualization, every feature is potentially a neighbor of every other feature, and with large datasets, the number of computations involved will be enormous. You should always try to include a Distance Band or Threshold Distance value when using the inverse distance conceptualizations. This is particularly important for large datasets. If you leave the Distance Band or Threshold Distance parameter blank, a threshold distance will be computed for you, but this may not be the most appropriate distance for your analysis; the default distance threshold will be the minimum distance that ensures every feature has at least one neighbor.
The FIXED_DISTANCE_BAND method works well for point data. It is the default option used by the Hot Spot Analysis (Getis-Ord Gi*) tool. It is often a good option for polygon data when there is a large variation in polygon size (very large polygons at the edge of the study area and very small polygons at the center of the study area, for example), and you want to ensure a consistent scale of analysis. See Selecting a fixed distance below for strategies to help you determine an appropriate distance band value for your analysis.
The ZONE_OF_INDIFFERENCE conceptualization works well when fixed distance is appropriate but imposing sharp boundaries on neighborhood relationships is not an accurate representation of your data. Keep in mind that the zone of indifference conceptual model considers every feature to be a neighbor of every other feature. Consequently, this option is not appropriate for large datasets since the Distance Band or Threshold Distance value supplied does not limit the number of neighbors but only specifies where the intensity of spatial relationships begins to wane.
The polygon contiguity conceptualizations (CONTIGUITY_EDGES_ONLY, CONTIGUITY_EDGES_CORNERS) are effective when polygons are similar in size and distribution, and when spatial relationships are a function of polygon proximity (the idea that if two polygons share a boundary, spatial interaction between them increases). When you select a polygon contiguity conceptualization, you will almost always want to select row standardization for tools that have the Row Standardization parameter.
The K_NEAREST_NEIGHBORS option is effective when you want to ensure you have a minimum number of neighbors for your analysis. Especially when the values associated with your features are skewed (are not normally distributed), it is important that each feature is evaluated within the context of at least eight or so neighbors (this is a rule of thumb only). When the distribution of your data varies across your study area so that some features are far away from all other features, this method works well. Note, however, that the spatial context of your analysis changes depending on variations in the sparsity/density of your features. When fixing the scale of analysis is less important than fixing the number of neighbors, the K nearest neighbors method is appropriate.
Some analysts consider DELAUNAY_TRIANGULATION a way to construct natural neighbors for a set of features. This method is a good option when your data includes island polygons (isolated polygons that do not share any boundaries with other polygons) or in cases where there is a very uneven spatial distribution of features. It is not appropriate when you have coincident features, however. Similar to the K nearest neighbors method, Delaunay triangulation ensures every feature has at least one neighbor but uses the distribution of the data itself to determine how many neighbors each feature gets.
The SPACE_TIME_WINDOW option allows you to define feature relationships in terms of both their spatial and their temporal proximity. You would use this option if you wanted to identify space-time hot spots, or construct groups where membership was constrained by space and time proximity. Examples of space-time analysis as well as strategies for effectively rendering the results from this type of analysis are provided in Space-Time Analysis.
For some applications, spatial interaction is best modeled in terms of travel time or travel distance. If you are modeling accessibility to urban services, for example, or looking for urban crime hot spots, modeling spatial relationships in terms of a network is a good option. Use the Generate Network Spatial Weights tool to create a spatial weights matrix file (.swm) prior to analysis; select GET_SPATIAL_WEIGHTS_FROM_FILE for your Conceptualization of Spatial Relationships value, then, for the Weights Matrix File parameter, provide the full path to the SWM file you created.
If none of the options for the Conceptualization of Spatial Relationships parameter work well for your analysis, you can create an ASCII text file or table with the feature-to-feature relationships you want and then use these to build a spatial weights matrix file. If one of the options above is close, but not perfect for your purposes, you can use the Generate Spatial Weights Matrix tool to create a basic SWM file, then edit your spatial weights matrix file.
Selecting a fixed-distance band value
Think of the fixed distance band you select as a moving window that momentarily settles on top of each feature and looks at that feature within the context of its neighbors. There are several guidelines to help you identify an appropriate distance band for analysis:
- Select a distance based on what you know about the geographic extent of the spatial processes promoting clustering for the phenomena you are studying. Often, you won't know this, but if you do, you should use your knowledge to select a distance value. Suppose, for example, you know that the average journey-to-work commute distance is 15 miles. Using 15 miles for the distance band is a good strategy for analyzing commuting data.
- Use a distance band that is large enough to ensure all features will have at least one neighbor, or results will not be valid. Especially if the input data is skewed (does not create a nice bell curve when you plot the values as a histogram), you will want to make sure that your distance band is neither too small (most features have only one or two neighbors) nor too large (several features include all other features as neighbors), because that would make resultant z-scores less reliable. The z-scores are reliable (even with skewed data) as long as the distance band is large enough to ensure several neighbors (approximately eight) for each feature. Even if none of the features have all other features as neighbors, performance issues and even potential memory limitations can result if you create a distance band where features have thousands of neighbors.
- Sometimes ensuring all features have at least one neighbor results in some features having many thousands of neighbors, and this is not ideal. This can happen when some of your features are spatial outliers. To resolve this problem, determine an appropriate distance band for all but the spatial outliers, and use the Generate Spatial Weights Matrix tool to create a spatial weights matrix file using that distance. When you run the Generate Spatial Weights Matrix tool, however, specify a minimum number of neighbors value for the Number of Neighbors parameter. Example: Suppose you are evaluating access to healthy food in Los Angeles County using census tract data. You know that more than 90 percent of the population live within three miles of shopping opportunities. If you are analyzing census tracts you will find that distances between tracts (based on tract centroids) in the downtown region are about 1,000 meters on average, but distances between tracts in outlying areas are more than 18,000 meters. To ensure every feature has at least one neighbor, your distance band would need to be more than 18,000 meters, and this scale of analysis (distance) is not appropriate for the questions you are asking. The solution is to create a spatial weights matrix file for the census tract feature class using the Generate Spatial Weights Matrix tool. Specify a Threshold Distance of about 4800 meters (approximately three miles) and a minimum number of neighbors value (let's say 2) for the Number of Neighbors parameter. This will apply the 4,800 meter fixed-distance neighborhood to all features except those that do not have a least two neighbors using that distance. For those outlier features (and only for those outlier features), the distance will be expanded just far enough to ensure every feature has at least two neighbors.
- Use a distance band that reflects maximum spatial autocorrelation. Whenever you see spatial clustering on the landscape, you are seeing evidence of underlying spatial processes at work. The distance band that exhibits maximum clustering, as measured by the Incremental Spatial Autocorrelation tool, is the distance where those spatial process are most active, or most pronounced. Run the Incremental Spatial Autocorrelation tool and note where the resulting z-scores seems to peak. Use the distance associated with the peak value for your analysis.
- Every peak represents a distance where the processes promoting spatial clustering are pronounced. Multiple peaks are common. Generally, the peaks associated with larger distances reflect broad trends (a broad east-to-west trend, for example, where the west is a giant hot spot and the east is a giant cold spot); generally, you will be most interested in peaks associated with smaller distances, often the first peak.
- An inconspicuous peak often means there are many different spatial processes operating at a variety of spatial scales. You probably want to look for other criteria to determine which fixed distance to use for your analysis (perhaps the most effective distance for remediation).
- If the z-score never peaks (in other words, it just keeps increasing) and if you are using aggregated data (for example, counties), it usually means the aggregation scheme is too coarse; the spatial processes of interest are operating at a scale that is smaller than the scale of your aggregation units. If you can move to a smaller scale of analysis (moving from counties to tracts, for example), this may help find a peak distance. If you are working with point data and the z-score never peaks, it means there are many different spatial processes operating at a variety of spatial scales and you will likely need to come up with different criteria for determining the fixed distance to use in your analysis. You will also want to check that your Beginning Distance when you run the Incremental Spatial Autocorrelation tool isn't too large.
- If you do not specify a beginning distance, the Incremental Spatial Autocorrelation tool will use the distance that ensures all features have at least one neighbor. If your data includes spatial outliers, that distance might be too large for your analysis, however, and may be the reason you do not see a pronounced peak in the Output Report File. The solution is to run the Incremental Spatial Autocorrelation tool on a selection set that temporarily excludes all spatial outliers. If a peak is found with the outliers excluded, use the strategy outlined above with that peak distance applied to all of your features (including the spatial outliers), and force each feature to have at least one or two neighbors. If you're not sure if any of your features are spatial outliers:
- For polygon data, render polygon areas using a Standard Deviation rendering scheme and consider polygons with areas that are greater than three standard deviations to be spatial outliers. You can use Calculate Field to create a field with polygon areas if you don't already have one.
- For point data, use the Near tool to compute each feature's nearest neighbor distance. To do this, set both the Input Features and Near Features to your point dataset. Once you have a field with nearest neighbor distances, render those values using a Standard Deviation rendering scheme and consider distances that are greater than three standard deviations to be spatial outliers.

Identify a distance where the processes promoting clustering are most pronounced. - Try not to get stuck on the idea that there is only one correct distance band. Reality is never that simple. Most likely, there are multiple/interacting spatial processes promoting observed clustering. Rather than thinking you need one distance band, think of the pattern analysis tools as effective methods for exploring spatial relationships at multiple spatial scales. Consider that when you change the scale (change the distance band value), you could be asking a different question. Suppose you are looking at income data. With small distance bands, you can examine neighborhood income patterns, middle scale distances might reflect community or city income patterns, and the largest distance bands would highlight broad regional income patterns.
Distance method
Many of the tools in the Spatial Statistics toolbox use distance in their calculations. These tools provide you with the choice of either Euclidean or Manhattan distance.
- Euclidean distance is calculated as
D = sq root [(x1–x2)**2.0 + (y1–y2)**2.0]where (x1, y1) is the coordinate for point A, (x2, y2) is the coordinate for point B, and D is the straight-line distance between points A and B.
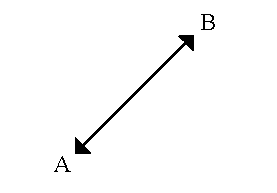
- Manhattan distance is calculated as
D = abs(x1–x2) + abs(y1–y2)where (x1, y1) is the coordinate for point A, (x2, y2) is the coordinate for point B, and D is the vertical plus horizontal difference between points A and B. It is the distance you must travel if you are restricted to north–south and east–west travel only. This method is generally more appropriate than Euclidean distance when travel is restricted to a street network and where actual street network travel costs are not available.
When your input features are not projected (i.e., when coordinates are given in degrees, minutes, and seconds) or when the output coordinate system is set to a Geographic Coordinate System, or when you specify an output feature class path to a feature dataset that has a Geographic Coordinate System spatial reference, distances will be computed using chordal measurements and the Distance Method parameter will be disabled. Chordal distance measurements are used because they can be computed quickly and provide very good estimates of true geodesic distances, at least for points within about thirty degrees of each other. Chordal distances are based on a sphere rather than the true oblate ellipsoid shape of the earth. Given any two points on the earth's surface, the chordal distance between them is the length of a line, passing through the three dimensional earth, to connect those two points. Chordal distances are reported in meters.
Self-potential (field giving intrazonal weight)
Several tools in the Spatial Statistics toolbox allow you to provide a field representing the weight to use for self-potential. Self-potential is the distance or weight between a feature and itself. Often, this weight is zero, but in some cases, you may want to specify another fixed value or a different value for every feature. If your conceptualization of spatial relationships is based on distances traveled within and among census tracts, for example, you might decide to model self-potential to reflect average intrazonal travel costs based on polygon size:
dii = 0.5*[(Ai / π)**0.5]where dii is the travel cost associated with intrazonal travel for polygon featurei, and Ai is the area associated with polygon featurei.
Standardization
Row standardization is recommended whenever the distribution of your features is potentially biased due to sampling design or an imposed aggregation scheme. When row standardization is selected, each weight is divided by its row sum (the sum of the weights of all neighboring features). Row standardized weighting is often used with fixed distance neighborhoods and almost always used for neighborhoods based on polygon contiguity. This is to mitigate bias due to features having different numbers of neighbors. Row standardization will scale all weights so they are between 0 and 1, creating a relative, rather than absolute, weighting scheme. Anytime you are working with polygon features representing administrative boundaries, you will likely want to choose the Row Standardization option.
Examples:
- Suppose you have a complete set of all crime incidents. In some parts of your study area there are lots of points because those are places with lots of crime. In other parts, there are few points, because those are low crime areas. The density of the points is a very good reflection (is representative) of what you're trying to understand: crime spatial patterns. You probably would not row standardize your spatial weights.
- Suppose you've taken soil samples. For some reason (the weather was nice or you happened to be in a location where you didn't have to climb fences, swim through swamps, or hike to the top of a mountain), you have lots of samples in some parts of the study area, but fewer in others. In other words, the density of your points is not strictly the result of a carefully planned random sample; some of your own biases may have been introduced. Further, where you have more points is not necessarily a reflection of the underlying spatial distribution of the data you're analyzing. To help minimize any bias that may have been introduced during the sampling process, you will want to row standardize your spatial weights. When you row standardize, the fact that one feature has two neighbors and another has 18 doesn't have a big impact on results; all the weights sum to 1.
- Whenever you aggregate your data, you are imposing a structure on it. Rarely will that structure be a good reflection of the data you are analyzing and the questions you are asking. For example, while census polygons (like census tracts) are designed around population, even if your analysis involves population-related questions, you will still likely row standardize your weights because those polygons represent just one of many ways they could have been drawn. With polygon data you will almost always want to row standardize your spatial weights.
Distance band or threshold distance
Distance Band or Threshold Distance sets the scale of analysis for most conceptualizations of spatial relationships (for example, INVERSE_DISTANCE and FIXED_DISTANCE_BAND). It is a positive numeric value representing a cutoff distance. Features outside the specified cutoff for a target feature are ignored in the analysis for that feature. With ZONE_OF_INDIFFERENCE, however, the influence of features outside the given distance is reduced in relation to proximity, while those inside the distance threshold are equally considered.
Choosing an appropriate distance is important. Some spatial statistics require each feature to have at least one neighbor for the analysis to be reliable. If the value you set for Distance Band or Threshold Distance is too small (so that some features have no neighbors), a warning message appears suggesting that you try again with a larger distance value. The Calculate Distance Band from Neighbor Count tool will evaluate minimum, average, and maximum distances for a specified number of neighbors and can help you determine an appropriate distance band value to use for analysis. See also Selecting a fixed distance band value for additional guidelines.
When no value is specified, a default threshold distance is computed. The table below indicates how different choices for the Conceptualization of Spatial Relationships parameter behave for each of three possible input types (negative values are not valid):
| Inverse Distance, Inverse Distance Squared | Fixed Distance Band, Zone of Indifference | Polygon Contiguity, Delaunay Triangulation, K Nearest Neighbors | |
|---|---|---|---|
| 0 | No threshold or cutoff is applied; every feature is a neighbor of every other feature. | Invalid. Runtime error will be generated. | Ignored. |
| blank | A default distance will be computed. This default will be the minimum distance to ensure that every feature has at least one neighbor. | A default distance will be computed. This default will be the minimum distance to ensure that every feature has at least one neighbor. | Ignored. |
| positive number | The nonzero, positive value specified will be used as a cutoff distance; neighbor relationships will only exist among features within this distance of each other. | For fixed distance band, only features within this specified cutoff of each other will be neighbors. For zone of indifference, features within this specified cutoff of each other will be neighbors; features outside the cutoff are neighbors too, but they are assigned a smaller and smaller weight/influence as distance increases. | Ignored. |
Number of neighbors
Specify a positive integer to represent the number of neighbors to include in the analysis for each target feature. When the value chosen for the Conceptualization of Spatial Relationships parameter is K Nearest Neighbors, each target feature will be evaluated within the context of the closest K features (where K is the number of neighbors specified). For Inverse Distance or Fixed Distance Band, when you run the Generate Spatial Weights Matrix tool, specifying a value for the Number of Neighbors parameter will ensure that each feature has a minimum of K neighbors. For the polygon contiguity methods, any feature that does not have the Number of Neighbors specified will get additional neighbors based on feature centroid proximity. For the Generate Network Spatial Weights tool, specifying a value for the Maximum Number of Neighbors parameter will ensure no feature has more than the value specified. For the Grouping Analysis tool, providing a value for the Number of Neighbors encourages feature proximity within each group. Specifying 6 neighbors, for example, will limit groups to features sharing at least one of six nearest neighbors to other features in the group.
Weights matrix file
Several tools allow you to define spatial relationships among features by providing a path to a spatial weights matrix file. Spatial weights are numbers that reflect the distance, time, or other cost between each feature and every other feature in the dataset. The spatial weights matrix file may be created using the Generate Spatial Weights Matrix tool or Generate Network Spatial Weights tool, or it may be a simple ASCII file.
When the spatial weights matrix file is a simple ASCII text file, the first line should be the name of a unique ID field. This gives you the flexibility to use any numeric field in your dataset as the ID when generating this file; however, the ID field must be type Integer (Long or Short) and have unique values for every feature. After the first line, the spatial weights file should be formatted into three columns:
- From feature ID
- To feature ID
- Weight
For example, suppose you have three gas stations. The field you are using as the ID field is called StationID, and the feature IDs are 1, 2, and 3. You want to model spatial relationships among these three gas stations using travel time in minutes. You could create an ASCII file that might look like the following:

Generally, when weights represent distance or time, they are inverted (for example, 1/10 when the distance is 10 miles or 10 minutes) so that nearer features have a larger weight than features that are farther away. Notice from the weights above that gas station 1 is 10 minutes from gas station 2. Notice also that travel time is not symmetrical in this example (traveling from gas station 1 to gas station 3 is 7 minutes, but traveling from gas station 3 to gas station 1 is only 6 minutes). Notice that the weight between gas station 1 and itself is 0 and that there is no entry for gas station 2 to itself. Missing entries are assumed to have a weight of 0.
Typing the values for the spatial weights matrix file can be a tedious job at best, even for small datasets. A better approach is to use the Generate Spatial Weights Matrix tool or to write a quick Python script to perform this task for you.
Spatial weights matrix file (.swm)
The Generate Spatial Weights Matrix or Generate Network Spatial Weights tool will create a spatial weights matrix file (.swm) defining the spatial relationships among all the features in your dataset based on the parameters you specify. This file is created in binary file format so the values in the file cannot be viewed directly. To view or edit the feature relationships in an SWM file, use the Convert Spatial Weights Matrix To Table tool.
When the spatial relationships among features is stored in a table, you may use the Generate Spatial Weights Matrix tool to convert that table into a spatial weights matrix file (.swm). The table will need the following fields:
| Field name | Description |
|---|---|
| <Unique ID field name> | An integer field that exists in the input feature class with a unique ID for each feature. This is the from feature ID. |
| NID | An integer field containing neighbor feature IDs. This is the to feature ID. |
| WEIGHT | This is the numeric weight quantifying the spatial relationship between the from and to features. Larger values reflect bigger weights and stronger influence, or interaction, between two features. |
Sharing spatial weights matrix files
The output from the Generate Spatial Weights Matrix and Generate Network Spatial Weights tools is an SWM file. This file is tied to the input feature class, the unique ID field, and the output coordinate system settings when the SWM file was created. Other people can duplicate the spatial relationships you define for analysis by using your SWM file and either the same input feature class, or a feature class linking all or a subset of the features to a matching Unique ID field. Especially if you plan to share your SWM files with others, try to avoid the situation where your output coordinate system differs from the spatial reference associated with your input feature class. A better strategy is to project the input feature class, then set the output coordinate system to Same as Input Feature Class prior to creating spatial weights matrix files.