Description
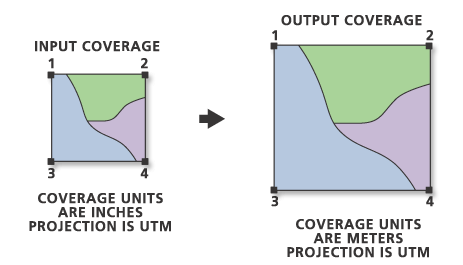
L'outil Transformer convertit des données d'un système de coordonnées vers un autre. Il est souvent utilisé pour convertir des couvertures créées en unités de numériseur (le plus souvent en pouces) en unités réelles représentées sur la minute topographique. Ces emplacements réels sont représentés par une projection spéciale ; par exemple, la projection de votre fond de carte peut être de type UTM avec des emplacements de points de contrôle mesurés en mètres.
Pour effectuer une transformation, vous devez être en mesure d'inscrire au moins deux tics de votre couverture dans des emplacements réels. Ces emplacements réels peuvent soit être mesurés en pieds ou en mètres à l'aide du système de coordonnées du fond de carte, soit être situés au niveau des intersections latitude-longitude. Si vos emplacements référencent des degrés de latitude et de longitude, utilisez l'outil Projeter pour convertir les points de contrôle dans le système de coordonnées qui correspond à votre fond de carte, mesuré en pieds ou en mètres. Effectuez cette opération avant de transformer la couverture numérisée.
Lors de leur transformation initiale, vos données sont transformées dans la même projection que votre carte source. Vous pourrez ensuite utiliser l'outil Projeter pour convertir la couverture dans une autre projection cartographique.
L'outil Transformer procède à la comparaison des coordonnées des tics de la couverture en entrée avec les coordonnées des tics correspondants dans la couverture en sortie. Les ID de tics identifient les tics à comparer. Le nombre minimal de tics nécessaires dépend de l'option de transformation utilisée. Les tics sont traités comme des points de contrôle pour la transformation et ils ne sont pas convertis avec l'équation de transformation. Les coordonnées des tics en sortie ne changent pas à l'issue de la transformation. Cependant, toute entité qui coïncide avec les tics en entrée ne coïncide généralement pas avec les tics en sortie. Un ajustement des entités peut s'avérer nécessaire pour les forcer à coïncider avec les tics de la couverture en sortie après la transformation.
L'outil Transformer utilise, par défaut, une fonction de transformation AFFINE pour transformer des coordonnées de couverture depuis la couverture en entrée vers la couverture en sortie. Au moins trois tics sont nécessaires pour calculer une transformation affine.
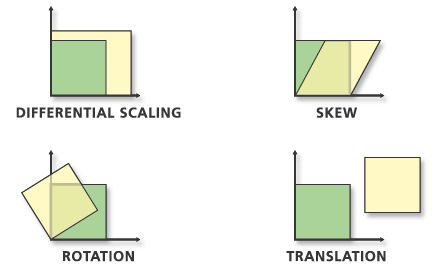
Une transformation affine permet de mettre à l'échelle en différé les données, de les désaxer, de les faire pivoter et de les convertir. Le graphique ci-après illustre les quatre changements possibles :
La fonction de transformation affine est la suivante :
x’ = Ax + By + CLes paramètres A à F sont déterminés par les points de contrôle,
y’ = Dx + Ey + Fpuis appliqués à toutes les coordonnées de la couverture.
où x et y sont les coordonnées de la couverture en entrée, et x' et y' les coordonnées de la couverture en sortie. A, B, C, D, E et F sont déterminés en comparant l'emplacement des tics dans la couverture en entrée et dans la couverture en sortie. Ces paramètres mettent à l'échelle, désaxent, font pivoter et convertissent les coordonnées de tic.
L'outil Transformer fournit un rapport sur les six paramètres et leur interprétation géométrique. Voici un exemple d'une partie du rapport en sortie pour une transformation affine.
Transformation de coordonnées pour la couverture in_cov_name
Scale (X,Y) = (246.140,255.702) Skew (degrees) = (-0.061)
Rotation (degrees) = (0.334) Translation = (2890.267,3679.906)
RMS Error (input, output) = (0.084,20.592)
Affine X = Ax + By + C
Y = Dx + Ey + F
A = 246.135 B = -1.763 C = 2890.267
D = 1.434 E = 255.696 F = 3679.906
Une section du rapport répertorie les paramètres des équations de transformation. Vous pouvez interpréter les paramètres de l'équation pour comprendre ce qu'il se passe d'un point de vue géométrique. La première section du rapport fournit les valeurs interprétées de la mise à l'échelle, de l'inclinaison et de la rotation. Le fait de changer l'ordre d'application de ces actions géométriques modifie leurs valeurs interprétées, mais n'a aucune incidence sur le résultat final et sur les paramètres de l'équation. L'interprétation utilisée respecte l'ordre suivant : (1) mise à l'échelle, (2) inclinaison dans la direction x et (3) rotation anti-horaire des points autour des axes. Les valeurs de conversion ne sont pas interprétées ; elles correspondent simplement aux paramètres de conversion C et F provenant des équations. L'outil Transformer interprète les paramètres de l'équation affine comme suit :
A = mx · cos t
B = my · (k · cos t - sin t)
D = mx · sin t
E = my · (k · sin t + cos t)
C = translation in x direction
F = translation in y direction
where
mx = change of scale in x direction
my = change of scale in y direction
k = shear factor along the x-axis = tan (skew angle) (the skew angle is measured from the y-axis)
t = rotation angle, measured counterclockwise from the x-axis
L'angle de rotation fait référence à la rotation des données autour d'un système de coordonnées x,y fixe. Si l'on se base sur la figure précédente, les données d'origine ont subi une rotation de 45 degrés. Une valeur négative signifie que les données pivotent dans le sens horaire par rapport à l'axe x.
La transformation d'HELMERT met à l'échelle, fait pivoter et convertit les données. Elle ne met pas à l'échelle indépendamment les axes et n'introduit pas de déformation. La transformation d'Helmert nécessite au moins deux points de contrôle. Le rapport suivant porte sur une transformation d'Helmert avec les mêmes couvertures que celles transformées précédemment avec une transformation affine.
Transformation de coordonnées pour la couverture in_cov_name
Scale (X,Y) = (249.927,249.927)
Rotation (degrees) = (0.362) Translation = (2855.407,3715.168)
RMS Error (input, output) = (0.118,29.398)
Similarity X = Ax + By + C
Y = -Bx + Ay + F
A = 249.922 B = -1.578
C = 2855.407 F = 3715.168
Comme vous pouvez le constater, les valeurs d'échelle X et Y sont identiques. Aucune valeur oblique n'est indiquée, car la transformation d'Helmert n'autorise pas l'introduction d'un quelconque mouvement non orthogonal dans les données.
La fonction de la transformation d'Herbert est la suivante :
x’ = Ax + By + C
y’ = -Bx + Ay + F
where
A = s · cos t
B = s · sin t
C = translation in x direction
F = translation in y direction
and
s = scale change (same in x and y directions)
t = rotation angle, measured counterclockwise from the x-axis
Comme pour la transformation AFFINE, l'angle de rotation fait référence à la rotation des données autour d'un système de coordonnée x,y fixe. Si l'on se base sur la figure précédente, les données d'origine ont subi une rotation de 45 degrés. Une valeur négative signifie que les données pivotent dans le sens horaire par rapport à l'axe x.
La transformation PROJECTIVE est établie à partir d'une formule plus complexe nécessitant au moins quatre tics.
x’ = (Ax + By + C) / (Gx + Hy + 1)
y’ = (Dx + Ey + F) / (Gx + Hy + 1)Le rapport PROJECTIF comprend l'échelle approximative, l'erreur QM et les paramètres de l'équation. En raison de la complexité de l'opération, les paramètres de transformation projective ne sont pas interprétés. Pour plus d'informations, reportez-vous à l'un des textes photogrammétriques répertoriés dans les références, à la fin de cette rubrique. Vous trouverez, ci-dessous, un exemple de rapport en sortie pour une transformation projective.
Transformation de coordonnées pour la couverture in_cov_name
Approximate scale = 1479.087
RMS Error (input, output) = (0.040,60.878)
2D Projective X = (Ax + By + C) / (Gx + Hy + 1)
Y = (Dx + Ey + F) / (Gx + Hy + 1)
A = 55.667 B = -718.999 C = 2125052.558
D = -199.525 E = 1385.541 F = 317759.475
G = -0.001 H = 0.000
Principal point of input (xp,yp) = (2.000,16.946)
Exposure center of output(Xc,Yc) = (2127791.000,343183.000)
Le point principal et le centre d'exposition correspondent au premier tic dans le fichier de tics de la couverture en entrée. Si vous souhaitez utiliser un autre point (le centre du jeu de données, par exemple), assurez-vous qu'il s'agit du premier tic du fichier.
Une erreur quadratique moyenne (EQM) est calculée pour chaque transformation effectuée ; elle indique la qualité de la transformation dérivée. L'exemple suivant illustre l'emplacement relatif de quatre points de contrôle en sortie (tics) et des points de contrôle en entrée transformés :
L'erreur QM mesure les erreurs entre les tics de la couverture en sortie et les emplacements transformés des tics de la couverture en entrée.
La transformation est dérivée à l'aide de la méthode de compensation par les moindres carrés, pour que soit créé un nombre de tics plus important que nécessaire.
L'erreur QM relative à chaque transformation est indiquée à la fois dans les unités de la couverture en entrée (0,031 pouce, par exemple) et dans les unités de la couverture en sortie (37,465 pieds, par exemple).
RMS Error (input, output) = (0.031,37.465)Une transformation parfaite produit une erreur QM de zéro. Bien que vous n'obtiendrez pas une valeur de 0,000, vous devez essayer de maintenir votre erreur QM à un niveau aussi bas que possible. Il est préférable de définir et de maintenir une erreur acceptable maximale. Les valeurs acceptables varient en fonction de la précision des données d'origine et de l'échelle de la carte source. Des erreurs QM élevées indiquent que les anciens et les nouveaux tics ne correspondent pas aux mêmes emplacements relatifs. Si votre erreur QM est plus élevée que la valeur établie, cela peut indiquer des problèmes de conversion susceptibles d'étirer erronément votre couverture en sortie.
La dernière partie du rapport répertorie les coordonnées des tics en entrée et en sortie, ainsi que leurs erreurs x et y (voir ci-dessous). Les paramètres de transformation constituent un compromis entre les tics en entrée et en sortie. Si vous appliquez les paramètres de transformation aux tics en entrée réels, les emplacements en sortie transformés ne correspondent pas aux véritables emplacements des tics en sortie. Les erreurs x et y représentent une mesure de la différence entre les véritables emplacements et les emplacements transformés des tics en sortie. Dans certains cas, il est possible de détecter un problème en observant les erreurs x et y.
tic id input x input y output x output y x error y error ------------------------------------------------------------------------ 1 2.000 16.946 2127791.000 343183.000 14.463 75.499 2 12.764 16.821 2143469.000 343326.000 -31.043 -85.363 3 2.052 1.976 2128000.000 320680.000 -36.290 -2.353 4 12.922 2.013 2143729.000 320912.000 20.245 -6.163 5 2.082 9.442 2127944.000 332015.000 22.016 -74.699 6 12.662 9.442 2143320.000 332015.000 10.609 93.079
Exemple
Cet exemple transforme une couverture exprimée en unités de numériseur en coordonnées réelles. La couverture d'origine nommée INCHCOV comporte les points de contrôle suivants, mesurés en pouces de numériseur :
IDTIC XTIC YTIC 1 2.000 16.946 2 12.764 16.821 3 2.052 1.976 4 12.922 2.013 5 2.082 9.442 6 12.662 9.442
Le fond de carte utilisé se trouvait dans le système de coordonnées State Plane avec des points de contrôle mesurés en pieds. Chaque tic correspond aux emplacements suivants :
Tic-IDs X Coordinates Y Coordinates 1 2,127,791 343,183 2 2,143,469 343,326 3 2,128,000 320,680 4 2,143,729 320,912 5 2,127,944 332,015 6 2,143,320 332,015
L'existence de la couverture en sortie est une condition préalable à l'exécution de l'outil Transformer. Utilisez l'outil Créer une couverture pour créer une couverture en sortie et copier, si vous le souhaitez, les fichiers TIC et BND de la couverture en entrée. Vous pouvez éventuellement utiliser l'outil Generate pour créer une couverture contenant des tics aux emplacements souhaités.
Le fichier de tics de la couverture en sortie doit contenir des coordonnées x,y de chaque tic à conserver dans cette couverture ; dans le cas présent, il s'agit des emplacements des tics dans le système de coordonnées State Plane. Les coordonnées des tics peuvent être ajustées dans ArcMap ou dans les modules TABLES ou INFO d'ArcInfo Workstation.
Une fois les nouveaux tics créés, les entités de la couverture numérisée peuvent être transformées en unités réelles. L'outil Transformer permet de convertir une couverture de projection State Plane référencée en pouces (INCHCOV) en une couverture de même type, mais référencée en pieds (STATECOV). Voici un exemple de transformation AFFINE.
Scale (X,Y) = (1452.317,1508.433) Skew (degrees) = (0.416)
Rotation (degrees) = (0.218) Translation = (2124994.654,317664.385)
RMS Error (input, output) = (0.048,71.614)
Affine X = Ax + By + C
Y = Dx + Ey + F
A = 1452.230 B = -5.526 C = 2124994.654
D = 15.858 E = 1508.462 F = 317664.385
tic id input x input y
output x output y x error y error
--------------------------------------------------
1 2.000 16.946
2127791.000 343183.000 14.463 75.499
2 12.764 16.821
2143469.000 343326.000 -31.043 -85.363
3 2.052 1.976
2128000.000 320680.000 -36.290 -2.353
4 12.922 2.013
2143729.000 320912.000 20.245 -6.163
5 2.082 9.442
2127944.000 332015.000 22.016 -74.699
6 12.662 9.442
2143320.000 332015.000 10.609 93.079
Voici l'exemple correspondant d'une transformation PROJECTIVE pour la même couverture. Pour rappel, l'option PROJECTIVE n'est généralement utilisée que lorsque les couvertures d'origine sont numérisées directement à partir de photos aériennes.
Transformation de coordonnées pour la couverture INCHCOV
Approximate scale = 1479.087
RMS Error (input, output) = (0.040,60.878)
2D Projective X = (Ax + By + C) / (Gx + Hy + 1)
Y = (Dx + Ey + F) / (Gx + Hy + 1)
A = 55.667 B = -718.999 C = 2125052.558
D = -199.525 E = 1385.541 F = 317759.475
G = -0.001 H = 0.000
Principal point of input (xp,yp) = (2.000,16.946)
Exposure center of output(Xc,Yc) = (2127791.000,343183.000)
tic id input x input y
output x output y x error y error
--------------------------------------------------
1 2.000 16.946
2127791.000 343183.000 -4.438 45.252
2 12.764 16.821
2143469.000 343326.000 -11.447 -36.202
3 2.052 1.976
2128000.000 320680.000 -17.300 46.421
4 12.922 2.013
2143729.000 320912.000 1.704 -36.962
5 2.082 9.442
2127944.000 332015.000 21.787 -93.410
6 12.662 9.442
2143320.000 332015.000 9.694 74.901
Enfin, voici la même couverture transformée à l'aide de l'option HELMERT.
Transformation de coordonnées pour la couverture inchcov
Scale (X,Y) = (1483.794,1483.794)
Rotation (degrees) = (0.377) Translation = (2124800.900,317942.729)
RMS Error (input,output) = (0.162,240.958)
Similarity X = Ax + By + C
Y = -Bx + Ay + F
A = 1483.762 B = -9.765
C = 2124800.900 F = 317942.729
tic id input x input y
output x output y x error y error
--------------------------------------------------
1 2.000 16.946
2127791.000 343183.000 -188.053 -76.916
2 12.764 16.821
2143469.000 343326.000 106.378 -300.277
3 2.052 1.976
2128000.000 320680.000 -173.717 214.680
4 12.922 2.013
2143729.000 320912.000 225.411 143.724
5 2.082 9.442
2127944.000 332015.000 -146.109 -42.262
6 12.662 9.442
2143320.000 332015.000 176.089 61.051
L'exemple suivant retourne une couverture à l'aide d'une transformation AFFINE.
Transformation de coordonnées pour la balise de couverture
Scale (X,Y) = (1.000,-1.000) Skew (degrees) = (0.000)
*** Negative Y scaling indicates reflection around X axis. ***
Rotation (degrees) = (180.000) Translation = (800.000,0.000)
RMS Error (input, output) = (0.000,0.000)
Affine X = Ax + By + C
Y = Dx + Ey + F
A = -1.000 B = 0.000 C = 800.000
D = 0.000 E = 1.000 F = 0.000
tic id input x input y
output x output y x error y error
--------------------------------------------------
1 700.000 100.000
100.000 100.000 0.000 0.000
2 700.000 800.000
100.000 800.000 0.000 0.000
3 100.000 800.000
700.000 800.000 0.000 0.000
4 100.000 100.000
700.000 100.000 0.000 0.000
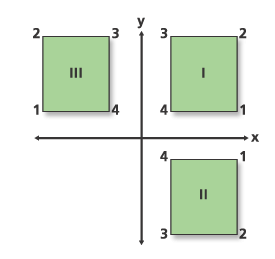
Notez le message relatif à la réflexion dans le rapport en sortie. La figure ci-après illustre ce qu'il advient de la couverture. Le rectangle étiqueté I est la couverture en entrée. Une échelle Y de -1 est appliquée aux coordonnées. Cela donne, comme résultat, le rectangle II. En l'absence de facteur d'inclinaison, les points pivotent de 180 degrés, ce qui place la couverture en position III. La dernière étape (non illustrée) consiste à convertir la couverture.
Bibliographie
Maling, D.H., Coordinate Systems and Map Projections. George Philip., 1973.
Maling, D.H., "Coordinate systems and map projections for GIS." In: Maguire D.J., M.F. Goodchild et D.W. Rhind (eds.), Geographical Information Systems: principles and applications. Vol. 1, pp. 135-146. Longman Group UK Ltd., 1991.
Moffitt, F.H. et E.M. Mikhail, Photogrammetry. Troisième édition. Harper and Row, Inc., 1980.
Pettofrezzo, A.J., Matrices and Transformations. Dover Publications, Inc., 1966.
Slama, C.C., C. Theurer et S.W. Henriksen (eds.), Manual of Photogrammetry. 4e édition. Chapitre XIV, pp. 729-731. ASPRS, 1980.