Mit der Geostatistical Analyst-Lizenz verfügbar.
Wie die Realisierungen generiert werden
Gaussian Geostatistical Simulations erstellt zunächst ein Raster an zufällig zugewiesenen Werten, die aus einer Standardnormalverteilung stammen (Mittelwert = 0 und Varianz = 1). Das Kovarianz-Modell (vom Semivariogramm, das im einfachen Kriging-Layer angegeben ist und als Eingabe für die Simulation benötigt wird) wird dann auf das Raster angewendet. Dadurch wird sichergestellt, dass Rasterwerte der räumlichen Struktur im Eingabe-Dataset entsprechen. Das resultierende Raster stellt eine Realisierung ohne Bedingungen dar und viele weitere können jeweils mithilfe eines anderen Rasters mit normalverteilten Werten erzeugt werden. Einzelheiten dieser Methode finden Sie in Dietrich and Newsam (1993).
Wenn eine bedingte Simulation ausgewählt wurde, werden die Raster ohne Bedingungen über Kriging mit Bedingungen versehen. Dieser Prozess verwendet die Kriging-Schätzung (Vorhersage) an jeder Position, um sicherzustellen, dass die simulierten Werte die Eingabedatenwerte berücksichtigen und die Kriging-Vorhersagen im Durchschnitt repliziert werden. Einzelheiten zur Aufbereitung der Realisierungen mithilfe von Kriging finden Sie in Journel (1974).
Wenn jedoch das einfache Kriging-Modell Messfehler beinhaltet, werden die Eingabedatenwerte nicht berücksichtigt (weder im einfachen Kriging-Layer noch in den simulierten Realisierungen). Außerdem wurde das Werkzeug "Gaussian Geostatistical Simulations" implementiert, um eine kontinuierliche (glatte) Suchnachbarschaft zu verwenden, die Unterbrechungen in den simulierten Oberflächen aufgrund von Änderungen der beim Kriging verwendeten lokalen Nachbarschaft vermeidet. Einzelheiten finden Sie in Aldworth (1998) sowie Gribov und Krivoruchko (2004).
Weitere Informationen zu Konzepten der geostatistischen Simulation und Beispiele für Simulationen mit und ohne Bedingungen finden Sie im Hilfeabschnitt unter Wichtige Konzepte der geostatistischen Simulation.
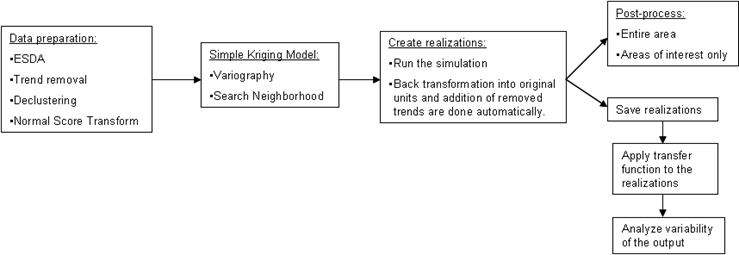
Zum allgemeinen Arbeitsablauf für Gaussian Geostatistical Simulation gehört das Vorbereiten der Daten, Erstellen der Realisierungen, Rückumwandlung der Ergebnisse in ursprüngliche Einheiten und Nachbearbeitung der Ergebnisse und/oder Verwenden der Ergebnisse als Eingabe für eine Transferfunktion (Modell), um Variabilität in der Ausgabe des Modells zu beurteilen. Dieser Vorgang wird in der folgenden Abbildung dargestellt:
Einfache Kriging-Modelle für Simulation
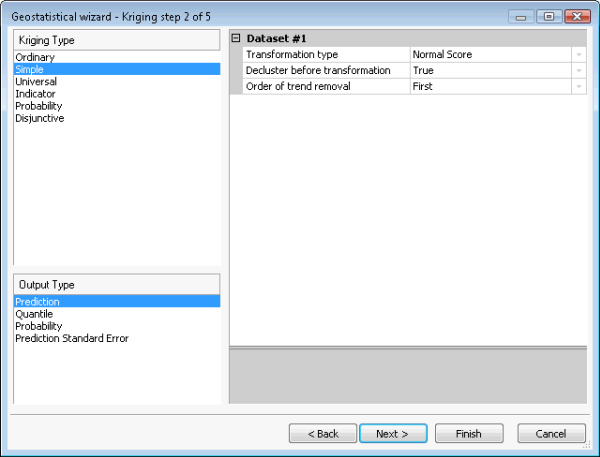
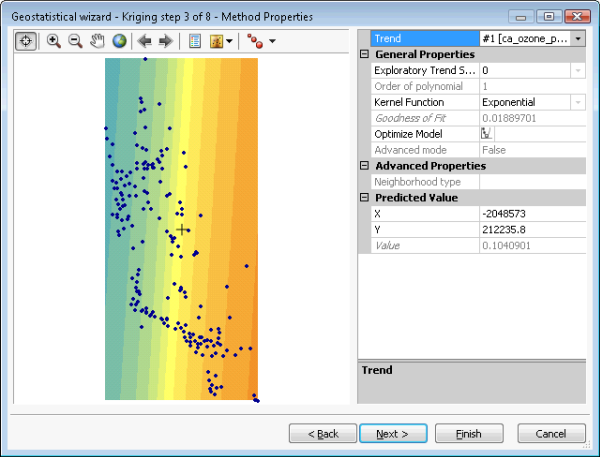
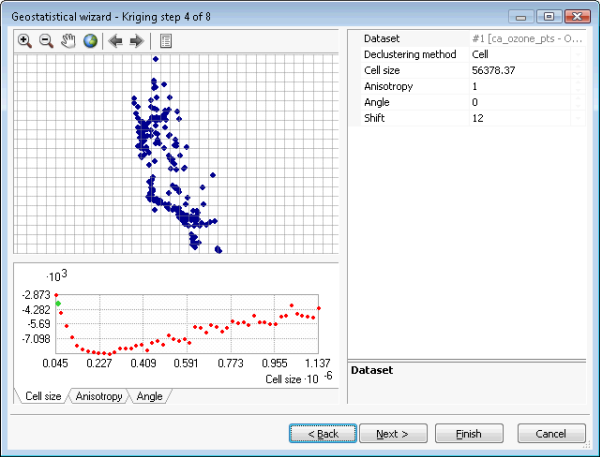
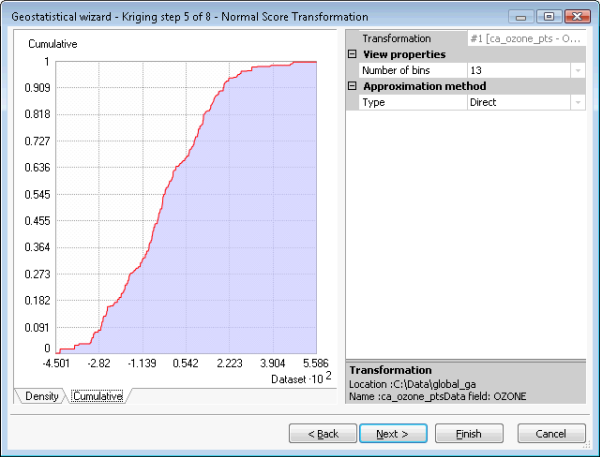
Das Werkzeug "Gaussian Geostatistical Simulation" akzeptiert jedes einfache Kriging-Modell. Simulationsergebnisse sind jedoch nur gültig, wenn die Eingabedaten (für Anpassung des Semivariogramms und Bedingungen für Realisierungen verwendet) normalverteilt sind. Dies kann durch Anwenden einer Normalverteilungstransformation erreicht werden. Cluster sollten aufgelöst werden, um ein repräsentatives Histogramm aus geclusterten Daten zu erhalten. Und Trends sollten entfernt werden, um sicherzustellen, dass der Mittelwert über die räumliche Domäne stationär ist. Diese Schritte werden in den folgenden Abbildungen illustriert. Abbildung (a) zeigt einfaches Kriging mit den ausgewählten Optionen für Trendentfernung, Cluster-Auflösung und Normalverteilungstransformation. Abbildung (b) zeigt den Trend, der vom Dataset entfernt wird, bevor Cluster-Auflösung, Normalverteilungstransformation und Variografie ausgeführt werden. Abbildung (c) zeigt die Cluster-Auflösung nach Zellen. Abbildung (d) zeigt die Normalverteilungstransformation, die in diesem Fall die direkte Methode verwendet.
Prüfen der Simulationsausgabe
Realisierungen sollten geprüft werden, um Folgendes zu bestätigen:
- Die Ausgabewerte, ihre räumlichen Muster und Positionen sind vernünftig.
- Das Histogramm der simulierten Daten reproduziert im Durchschnitt das Histogramm der Eingabedaten.
- Die Semivariogramme der simulierten Daten reproduzieren im Durchschnitt das Semivariogramm der Eingabedaten.
- Für Simulationen mit Bedingungen werden die Eingabedatenwerte berücksichtigt (es sei denn, das einfache Kriging-Modell umfasst Messfehler).
Nachbearbeitung
Sobald die Realisierungen erstellt wurden, werden sie gewöhnlich nachbearbeitet, um Zusammenfassungen der Ergebnisse zu erhalten. Das Werkzeug "Gaussian Geostatistical Simulations" bietet mehrere Nachbearbeitungsoptionen, die für die gesamte räumliche Ausdehnung der Raster oder in Bereichen von besonderem Interesse ausgeführt werden können. Diese Bereiche werden durch die Angabe einer Polygon-Feature-Class in der Option "Input statistical polygons" des Werkzeugs definiert. Die Ausgabe ist in beiden Fällen ähnlich: Die Nachbearbeitung der gesamten Raster erzeugt Zusammenfassungen von Rastern, während die Nachbearbeitung von Polygonbereichen eine Polygon-Ausgabe-Feature-Class erzeugt, die zusammenfassende Statistiken für jedes Polygon enthält.
Nachbearbeitung der vollständigen Rasterausdehnung
- Ausgaberaster umfassen den Minimalwert, der für jede Position (Zelle) erstellt wird, sowie das Maximum, den Mittelwert, die Standardabweichung, das erste Quartil, den Medianwert (zweites Quartil) und das dritte Quartil. Zusätzlich können Sie ein Quantil angeben, das einen Wert zurückgibt, der basierend auf der in jeder Zelle simulierten Werteverteilung diesem Quantil entspricht. Sie können auch einen Schwellenwert angeben, der den Prozentsatz der simulierten Werte liefert, die den Schwellenwert für jede Zelle überschreiten.
- Beachten Sie, dass die nachzubearbeitende Ausdehnung durch die Angabe eines Begrenzungspolygons oder eine Gruppe von Punkten begrenzt werden kann. (In diesem Fall wird eine konvexe Hülle generiert und als Begrenzungspolygon verwendet.) Die Werte werden nur innerhalb des Begrenzungspolygons simuliert.
Nachbearbeitung für Interessenbereiche
- Bei der Angabe von polygonalen Interessenbereichen umfasst die Ausgabe für jedes Polygon automatisch die Summenstatistik, die in der folgenden Tabelle erläutert wird. Zusätzlich können Sie einen Quantil- und einen Schwellenwert angeben (wie bei der Nachbearbeitung der vollständigen Rasterausdehnung). Die erzeugte Ausgabe, wenn diese Optionen ausgewählt sind, wird ebenfalls in der Tabelle beschrieben.
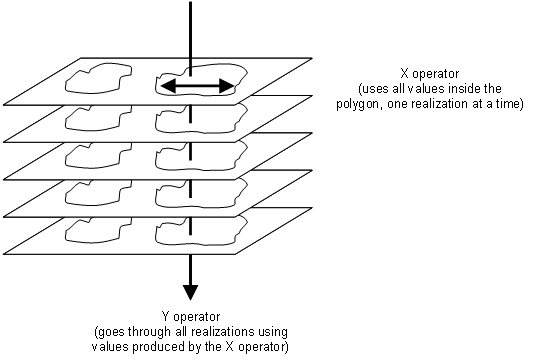
- Die Berechnung der zusammengefassten Ausgabe für diese Polygone erfolgt mit Operatoren wie in der Abbildung unten dargestellt. Der X-Operator verwendet alle Werte, die innerhalb des Polygons liegen, und berechnet einen Wert für jede Realisierung. Der Y-Operator verwendet Werte aus allen Realisierungen. Eingaben für den Y-Operator sind die Werte für die Polygonbereiche jeder Realisierung, die vom X-Operator berechnet wurden.
Die Bedeutungen der Felder in der Ausgabe-Feature-Class werden in der folgenden Tabelle aufgelistet.
| Feldname | Beschreibung |
|---|---|
MIN | Minimalwert jeder Zelle in allen Realisierungen, die innerhalb des Polygons liegen. |
MAX | Maximalwert jeder Zelle in allen Realisierungen, die innerhalb des Polygons liegen. |
MEAN | Mittelwert aller Zellen in allen Realisierungen, die innerhalb des Polygons liegen. |
STDDEV | Standardabweichung aller Zellen in allen Realisierungen, die innerhalb des Polygons liegen. |
QUARTILE1 | Erster Quartilwert aller Zellen in allen Realisierungen, die innerhalb des Polygons liegen. |
MEDIAN | Medianwert aller Zellen in allen Realisierungen, die innerhalb des Polygons liegen. |
QUARTILE3 | Dritter Quartilwert aller Zellen in allen Realisierungen, die innerhalb des Polygons liegen. |
QUANTILE | Wert, der einem vom Benutzer angegebenen Quantil für alle Zellen in allen Realisierungen entspricht, die innerhalb des Polygons liegen. |
P_THRSHLD | Prozentsatz der Zellen, die einen vom Benutzer angegebenen Schwellenwert überschreiten, basierend auf allen Zellen in allen Realisierungen, die innerhalb des Polygons liegen. |
X_Y | Die X-Funktion wird jeweils für eine Realisierung auf die Werte der Zellen angewendet, die innerhalb des Polygons liegen. Der Prozess entspricht der Ausführung des Werkzeugs "Zonal Statistics" mit dem Polygon als Zone und jeweils einer Realisierung als Werteraster. Die Y-Funktion wird auf die Werte angewendet, die durch die X-Funktion erzeugt wurden.
|
CELL_COUNT | Anzahl der Zellen, die innerhalb des Polygons liegen. Wenn der Zellenmittelpunkt innerhalb des Polygons liegt, wird diese Zelle ebenfalls als innerhalb des Polygons liegend betrachtet. Eine negative Anzahl deutet darauf hin, dass ein Teil des Polygons außerhalb der Ausdehnung des simulierten Rasters und/oder außerhalb der Ausschneidebegrenzung liegt. Die negative Zahl selbst gibt die Gesamtzahl der Zellen an, die innerhalb des Polygons liegen. |
SOURCE_ID | Die Objekt- oder Feature-ID der Eingabepolygon-Feature-Class. |
Für die beiden Optionen "Begrenzungspolygon" und "Polygonale Interessenbereiche" wird für Rasterzellen angenommen, dass sie innerhalb der Polygone liegen, wenn die Zellenmittelpunkte innerhalb der Polygonbegrenzung liegen.
Beispiel für eine bedingte Simulation und Nachbearbeitungsausgabe
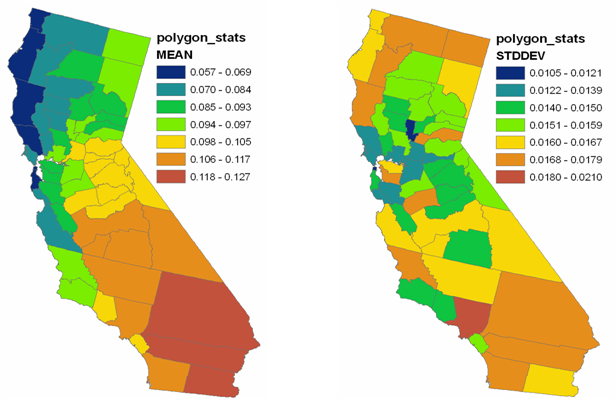
Die folgende Abbildung zeigt das Ergebnis einer bedingten Simulation mit Polygonnachbearbeitung der Ausgabe. Die Karten zeigen den Mittelwert und die Standardabweichung von 100 Realisierungen von Ozonwerten für jeden Landkreis in Kalifornien. Diese Werte von Mittelwert und Standardabweichung könnten beispielsweise in epidemiologischen Studien verwendet werden, in denen das Auftreten einer Krankheit mit dem durchschnittlichen Ozonwert für jeden Landkreis verglichen werden soll.
Literaturhinweise
Aldworth, J. 1998. Spatial Prediction, Spatial Sampling, and Measurement Error. Ph.D. Thesis, Iowa State University. 186.
Chiles, J. P., und P. Delfiner. 1999. Geostatistics: Modeling Spatial Uncertainty. New York: John Wiley & Sons, 449–471.
Deutsch, C. V., und A. G. Journel. 1998. GSLIB Geostatistical Software Library and User's Guide, 2nd Edition. New York: Oxford University Press, 119–141.
Dietrich, C. R., und G. N. Newsam. 1993. "A Fast and Exact Method for Multidimensional Gaussian Stochastic Simulations." Water Resources Research 29 (8): 2861–2869.
Goodchild, M. F., B. O. Parks und L. T. Steyaert. 1993. Environmental Modeling with GIS. New York: Oxford University Press, 432–437.
Gribov, A. und K. Krivoruchko. 2004. "Geostatistical Mapping with Continuous Moving Neighborhood." Mathematical Geology 36 (2): 267–281.
Journel, A. G. 1974. "Geostatistics for Conditional Simulation of Ore Bodies." Economic Geology 69: 673–687.
Leuangthong, O., J. A. McLennan und C. V. Deutsch. 2004. "Minimum Acceptance Criteria for Geostatistical Realizations." Natural Resources Research 13 (3): 131–141.