Mit der Spatial Analyst-Lizenz verfügbar.
Für jede Zelle berechnet das Werkzeug Neigung die maximale Änderungsrate des Wertes dieser Zelle im Vergleich zu ihren benachbarten Zellen. Das steilste Gefälle für die Zelle ist durch die maximale Änderung der Höhe entlang der Entfernung zwischen der Zelle und ihren acht Nachbarzellen gekennzeichnet.
Vom Konzept her passt das Werkzeug eine Ebene an die Z-Werte einer aus 3 x 3 Zellen bestehenden Zellengruppe um die bearbeitete Zelle bzw. die mittlere Zelle herum an. Der Neigungswert dieser Ebene wird anhand der durchschnittlichen Maximalwertmethode berechnet (siehe Referenzliste). Die Richtung der Ebene entspricht der Ausrichtung der bearbeiteten Zelle. Je niedriger der Neigungswert, desto flacher das Gelände. Je höher der Neigungswert, desto steiler das Gelände.
Wenn es eine Zellenposition in der Nachbarschaft mit einem NoData-Z-Wert gibt, wird der Z-Wert der Mittelzelle dieser Position zugewiesen. Am Rand des Rasters enthalten mindestens drei Zellen (außerhalb der Ausdehnung des Rasters) "NoData" als Z-Wert. Diesen Zellen wird der Z-Wert der Mittelzelle zugewiesen. Das Ergebnis ist eine Abflachung der 3 x 3-Ebene, die an diese Randzellen angepasst wird, was üblicherweise zu einer Verringerung der Neigung führt.
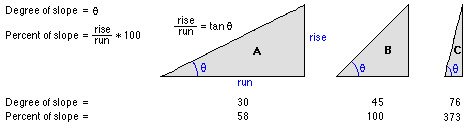
Die Neigung des Ausgabe-Rasters kann in Grad oder Prozent (prozentuale Steigung) berechnet werden. Die prozentuale Steigung ist einfacher zu verstehen, wenn Sie diese als Steigung, geteilt durch die Entfernung, multipliziert mit 100, betrachten. Siehe Dreieck B unten. Bei einem Winkel von 45 Grad entspricht die Steigung der Entfernung, und die prozentuale Steigung beträgt 100 Prozent. Wenn die Neigung sich der Vertikalen (90 Grad) annähert, wie im Falle von Dreieck C, geht die prozentuale Neigung ins Unendliche.
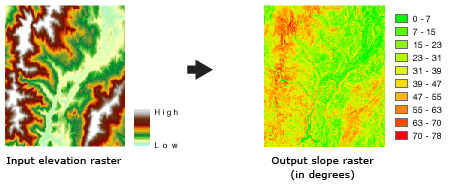
Das Werkzeug Neigung wird am häufigsten auf Höhen-Datasets angewendet (siehe das folgende Diagramm). Steilere Neigungen sind im Ausgabe-Neigungs-Raster rot schattiert.
Das Werkzeug kann auch zusammen mit anderen Typen kontinuierlicher Daten, wie z. B. Bevölkerungsdaten, verwendet werden, um einschneidende Wertänderungen zu ermitteln.
Der Neigungsalgorithmus
Die Änderungsraten (Delta) der Oberfläche in der horizontalen (dz/dx) und der vertikalen (dz/dy) Richtung von der Mittelzelle bestimmen die Neigung. Der Basisalgorithmus zum Berechnen der Neigung lautet:
slope_radians = ATAN ( √ ([dz/dx]2 + [dz/dy]2) )Die Neigung wird in der Regel unter Verwendung des folgenden Algorithmus in Einheiten von Grad gemessen:
slope_degrees = ATAN ( √ ([dz/dx]2 + [dz/dy]2) ) * 57.29578Der Neigungsalgorithmus kann auch wie folgt interpretiert werden:
slope_degrees = ATAN (rise_run) * 57.29578- Dabei gilt:
rise_run = √ ([dz/dx]2 + [dz/dy]2]
Die Werte der Mittelzelle und ihrer acht benachbarten Zellen bestimmen die horizontalen und vertikalen Deltas. Die Nachbarn werden als Buchstaben a bis i identifiziert, wobei e die Zelle darstellt, für die die Ausrichtung berechnet wird.
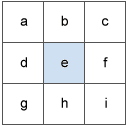
Die Änderungsrate in der x-Richtung für Zelle e wird mit dem folgenden Algorithmus berechnet:
[dz/dx] = ((c + 2f + i) - (a + 2d + g) / (8 * x_cellsize)Die Änderungsrate in der y-Richtung für Zelle e wird mit dem folgenden Algorithmus berechnet:
[dz/dy] = ((g + 2h + i) - (a + 2b + c)) / (8 * y_cellsize)Ein Beispiel für eine Neigungsberechnung
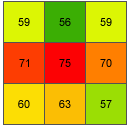
Beispiel: Der Neigungswert der mittleren Zelle des unten dargestellten beweglichen Fensters wird berechnet.
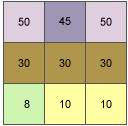
Die Zellengröße beträgt 5 Einheiten. Standardmäßig wird Grad als Neigungseinheit verwendet.
Die Änderungsrate in der x-Richtung für die mittlere Zelle e lautet:
[dz/dx] = ((c + 2f + i) - (a + 2d + g) / (8 * x_cellsize)
= ((50 + 60 + 10) - (50 + 60 + 8)) / (8 * 5)
= (120 - 118) / 40
= 0.05Die Änderungsrate in der y-Richtung für die Zelle e lautet:
[dz/dy] = ((g + 2h + i) - (a + 2b + c)) / (8 * y_cellsize)
= ((8 + 20 + 10) - (50 + 90 + 50)) / (8 * 5)
= (38 - 190 ) / 40
= -3.8Mit den Änderungsraten in der x- und der y-Richtung für Zelle e wird die Neigung für die mittlere Zelle mit dem folgenden Algorithmus berechnet:
rise_run = √ ([dz/dx]2 + [dz/dy]2)
= √ ((0.05)2 + (-3.8)2)
= √ (0.0025 + 14.44)
= 3.80032 slope_degrees = ATAN (rise_run) * 57.29578
= ATAN (3.80032) * 57.29578
= 1.31349 * 57.29578
= 75.25762Der ganzzahlige Neigungswert für Zelle e beträgt 75 Grad.
Referenzliste
Burrough, P. A., and McDonell, R. A., 1998. Principles of Geographical Information Systems (Oxford University Press, New York), 190 pp.