Mit der Geostatistical Analyst-Lizenz verfügbar.
Das Semivariogramm stellt die räumliche Autokorrelation der gemessenen Referenzpunkte dar. Sobald jedes Positionspaar geplottet ist (Binning des empirischen Semivariogramms), wird ein Modell durch diese Positionen angepasst (Anpassen eines Modells an das empirische Semivariogramm). Es gibt bestimmte Merkmale, die häufig zum Beschreiben dieser Modelle verwendet werden.
Bereich und Sill
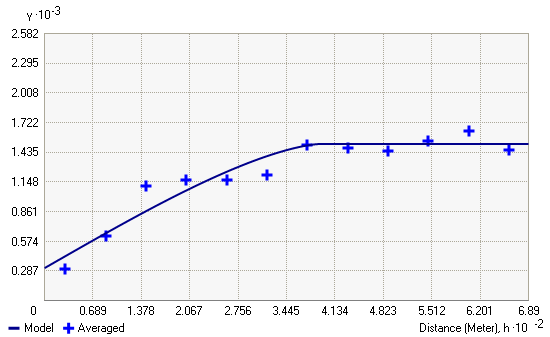
Wenn Sie das Modell eines Semivariogramms betrachten, werden Sie bemerken, dass das Modell ab einer bestimmten Entfernung abflacht. Die Entfernung, an der das Modell zuerst abflacht, wird als "Major Range" bezeichnet. Referenzpositionen, die durch Entfernungen getrennt sind, die innerhalb des Bereiches liegen, sind räumlich korreliert, Positionen außerhalb des Bereiches dagegen nicht.
Der Wert, bei dem das Semivariogramm den Bereich erreicht (den Wert auf der Y-Achse), wird als "Sill" bezeichnet. Ein "Partial Sill" ergibt sich aus "Sill" minus "Nugget".
Das Nugget
Theoretisch beträgt bei einer Trennungsentfernung von null (z. B. Lag = 0) der Semivariogrammwert 0. Bei einer unendlich kleinen Trennungsentfernung weist das Semivariogramm jedoch oft einen Nugget-Effekt auf, d. h. einen Wert größer als 0. Wenn beispielsweise das Semivariogramm-Modell die Y-Achse bei 2 schneidet, beträgt der Nugget-Wert 2.
Der Nugget-Effekt lässt sich auf Messfehler und/oder räumliche Schwankungen bei Entfernungen zurückführen, die kleiner als das Abtastintervall sind. Der Messfehler tritt aufgrund eines in Messgeräten inhärenten Fehlers auf. Natürliche Phänomene können bei verschiedenen Maßstäben räumlich variieren. Variationen bei Mikromaßstäben, die kleiner als die Abtastschrittweiten sind, erscheinen als Teil des Nugget-Effekts. Vor der Datenerfassung sollten Sie sich mit den Maßstäben räumlicher Variation vertraut machen.