Unabhängig davon, ob Sie die Erde als Kugel oder Sphäroid darstellen, müssen Sie die dreidimensionale Erdoberfläche auf ein zweidimensionales Kartenblatt übertragen. Diese mathematische Transformation wird im Allgemeinen als Kartenprojektion bezeichnet. Sie können sich die Veränderungen der räumlichen Eigenschaften durch Kartenprojektionen wie eine Lichtquelle vorstellen, die durch die Erde hindurch auf eine Oberfläche scheint, die so genannte Projektionsfläche. Stellen Sie sich eine leere Erdoberfläche vor, auf der nur das Gradnetz zu sehen ist. Wickeln Sie ein Blatt Papier um die Erde. Eine Lichtquelle im Erdmittelpunkt wirft nun die Schatten des Gradnetzes auf das Papier. Wenn Sie nun das Papier entfernen und flach ausbreiten, sehen Sie, dass die Form des Gradnetzes auf dem flachen Papier sich von der Form des Gradnetzes auf der Erde unterscheidet. Die Kartenprojektion hat das Gradnetz verzerrt.
Ein Sphäroid kann genauso wenig auf eine Fläche abgeplattet werden wie eine Orangenschale. Es treten unweigerlich Risse auf. Die zweidimensionale Darstellung der Erdoberfläche führt zu Verzerrungen der Formen, Flächen, Entfernungen oder Richtungen der Daten.
Bei Kartenprojektionen werden mathematische Formeln verwendet, um sphäroidische Koordinaten auf dem Globus in flache planare Koordinaten umzurechnen.
Unterschiedliche Projektionen führen zu unterschiedlichen Arten von Verzerrungen. Einige Projektionen sind so angelegt, dass die Verzerrungen einer oder zweier Dateneigenschaften minimiert werden. So kann eine Projektion beispielsweise die Fläche eines Features bewahren, die Form jedoch verfälschen. In der nachfolgenden Grafik sind die Daten in der Nähe der Pole gestreckt.
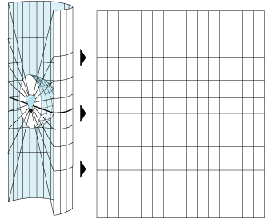
Das folgende Diagramm zeigt, wie dreidimensionale Features komprimiert werden, um auf eine flache Oberfläche zu passen.
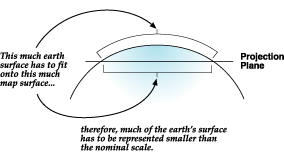
Kartenprojektionen sind für bestimmte Zwecke konzipiert. Einige werden zum Beispiel für Daten mit großem Maßstab in einer beschränkten Fläche verwendet, während andere zur Erstellung einer Weltkarte mit kleinem Maßstab dienen. Kartenprojektionen für Daten mit kleinem Maßstab basieren in der Regel auf kugeligen statt auf sphäroidischen geographischen Koordinatensystemen.
Winkeltreue Projektionen
Winkeltreue Projektionen bewahren die lokale Form. Um einzelne Winkel beizubehalten, die die räumlichen Beziehungen beschreiben, muss eine winkeltreue Projektion die Gradnetzlinien anzeigen, die sich an 90-Grad-Winkeln auf der Karte überschneiden. Eine Kartenprojektion ermöglicht dies, indem sie alle Winkel beibehält. Der Nachteil besteht darin, dass eine durch mehrere Bögen eingeschlossene Fläche möglicherweise stark verzerrt wird. Es gibt keine Kartenprojektion, die die Form großer Gebiete korrekt darstellen kann.
Flächentreue Projektionen
Flächentreue Projektionen bewahren die Fläche der angezeigten Features. Hierzu werden die anderen Eigenschaften wie Form, Winkel und Maßstab verzerrt. In flächentreuen Projektionen überschneiden die Meridiane und die Parallelen sich möglicherweise nicht in Winkeln von 90 Grad. In einigen Fällen, insbesondere bei Karten kleinerer Regionen, erscheinen Formen nicht offensichtlich verzerrt. Daher kann es schwierig sein, eine flächentreue Projektion von einer winkeltreuen Projektion zu unterscheiden, sofern dies nicht dokumentiert oder gemessen wird.
Äquidistante Projektionen
Äquidistante Karten bewahren die Entfernungen zwischen bestimmten Punkten. Der Maßstab wird bei keiner Projektion überall auf der ganzen Karte korrekt beibehalten. Es gibt jedoch in den meisten Fällen eine oder mehrere Linien auf einer Karte, an denen der Maßstab ordnungsgemäß beibehalten wird. Die meisten äquidistanten Projektionen weisen eine oder mehrere Linien auf, deren Länge auf einer Karte der gleichen Länge (bei Kartenmaßstab) wie auf dem Globus entspricht, unabhängig davon, ob es sich bei der Linie um einen großen oder kleinen Kreis oder eine gerade oder gebogene Linie handelt. Solche Entfernungen gelten als wahr. Bei der Sinusoidal-Projektion z. B. bilden der Äquator und alle Parallelen ihre wahren Längen ab. In anderen äquidistanten Projektionen weisen der Äquator und alle Meridiane korrekte Längenwerte auf. Wieder andere (z. B. die äquidistante Zwei-Punkt-Projektion) zeigen den tatsächlichen Maßstab zwischen einem oder zwei Punkten und jedem anderen Punkt auf der Karte. Bedenken Sie stets, dass keine Projektion für alle Punkte auf einer Karte äquidistant ist.
Wahre Richtungsprojektionen
Die kürzeste Route zwischen zwei Punkten auf einer gekrümmten Oberfläche wie der Erde ist die sphäroidische Entsprechung einer geraden Linie auf einer flachen Oberfläche. Damit ist der große Kreis gemeint, auf dem die zwei Punkte liegen. Wahre Richtungsprojektionen oder azimutale Projektionen bewahren einige der großen Kreisbögen und geben die Richtungen oder die Azimute aller Punkte in Bezug auf den Mittelpunkt der Karte korrekt an. Einige wahre Richtungsprojektionen sind zudem winkeltreu, flächentreu oder äquidistant.