Im Folgenden sind die verfügbaren Verteilungen verschiedener Werkzeuge angegeben, die Zufallswerte erstellen. Die Verteilungen transformieren die vom angegebenen Strom (global in der Analyseumgebung oder aber lokal für das Werkzeug festgelegt) erzeugten Zufallswerte 0 oder 1 in die angegebene Verteilung. Die Syntax und Parameter für die einzelnen Verteilungen finden Sie unter Die Verteilungssyntax für Zufallswerte.
Gleichmäßige Verteilung
Die gleichmäßige Verteilung ist eine kontinuierliche Wahrscheinlichkeitsfunktion, in der alle Werte innerhalb eines bestimmten Intervalls dieselbe Wahrscheinlichkeit aufweisen. Eine Ganzzahlverteilung ist eine diskrete Version der gleichmäßigen Verteilung (siehe unten). Die gleichmäßige Verteilung kann zum Modellieren der Konzentration eines Gases in einem Simulationsmodell oder der Zeit zwischen Unfällen auf einer Kreuzung oder auch zum Platzieren der Punkte im Werkzeug "Zufällige Punkte erstellen" verwendet werden.
Die gleichmäßige Verteilung wird häufig zum Modellieren zufälliger Ereignisse verwendet, wenn jedes potenzielle Ergebnis oder Auftreten dieselbe Vorkommenswahrscheinlichkeit besitzt.
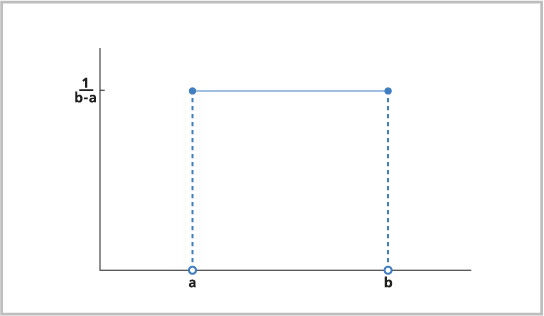
Für die gleichmäßige Verteilung gilt die folgende Formel:
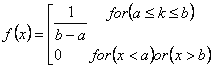
wobei
a ist der minimale Wert für das Intervall mit gleicher Wahrscheinlichkeit.
b ist der maximale Wert für das Intervall mit gleicher Wahrscheinlichkeit.
x steht für die Beobachtungen.
Die ausgewählten Zufallswerte liegen zwischen dem Minimum und dem Maximum (jeweils exklusive). Das Minimum muss kleiner als das Maximum sein. Wenn das Minimum und das Maximum nicht angegeben sind, werden gleichmäßige Variablen zwischen 0,0 und 1,0 produziert.
Ganzzahlverteilung
Die Ganzzahlverteilung ist eine kontinuierliche Wahrscheinlichkeitsfunktion, bei der alle diskreten Werte innerhalb eines bestimmten Intervalls dieselbe Wahrscheinlichkeit aufweisen. Die Ganzzahlverteilung ist die diskrete Version der gleichmäßigen Verteilung (siehe oben). Sie können die Ganzzahlverteilung zum Modellieren der Vorkommenswahrscheinlichkeit der einzelnen Zahlen beim Würfeln (jede Zahl hat eine Vorkommenswahrscheinlichkeit von einem Sechstel), zum Modellieren zufälliger Ereignisse in einem Simulationsmodell oder zum Auswählen von Stichprobenstellen für eine biologische Untersuchung verwenden.
Die Ganzzahlverteilung wird häufig zum Modellieren zufälliger Ereignisse verwendet, wenn jedes potenzielle Ergebnis oder Auftreten dieselbe Vorkommenswahrscheinlichkeit besitzt.
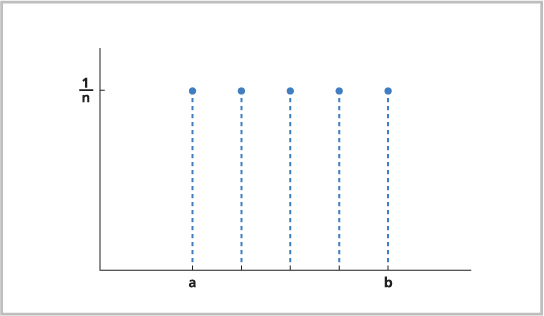
Für die Ganzzahlverteilung gilt die folgende Formel:
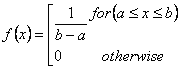
wobei
a ist der minimale Wert für das Intervall mit gleicher Wahrscheinlichkeit.
b ist der maximale Wert für das Intervall mit gleicher Wahrscheinlichkeit.
x steht für die Beobachtungen.
Die ausgewählten Zufallswerte liegen zwischen dem Minimum und dem Maximum (jeweils exklusive). Das Minimum muss kleiner als das Maximum sein. Wenn das Minimum und das Maximum nicht angegeben sind, werden gleichmäßige Werte zwischen 1 und 100 erzeugt.
Normalverteilung
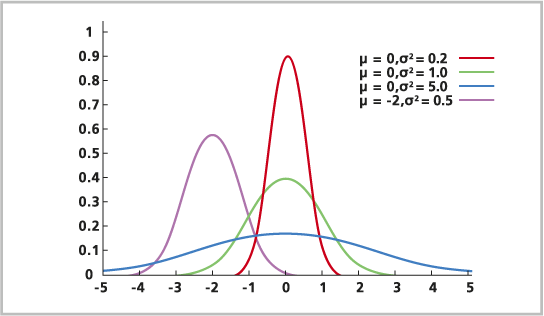
Mit der Normalverteilung werden häufig auftretende kontinuierliche Zufallsvariablen modelliert. Die Normalverteilung wird häufig verwendet und ist für viele Anwendungen geeignet. Sie beruht auf dem Zentralen Grenzwertsatz, der seinerseits auf dem Prinzip basiert, dass die Summe der Zufallsvariablen bei einer großen Anzahl von Beobachtungen normal verteilt ist. Zum Beispiel nähert sich die Häufigkeit, mit der beim Werfen einer Münze "Kopf" fällt, der Normalverteilung, wenn die Münze sehr oft geworfen wird. Beispiele für Normalverteilungen sind die Größe der Menschen in einem Land, Höhenwerte in einem Bundesland und Ergebnisse von Mathematiktests bei allen 12 Jahre alten Schülern.
Für die Normalverteilung gilt die folgende Formel:
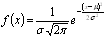
wobei
μ ist der Mittelwert.
σ ist die Standardabweichung (eine positive Zahl).
Die Normalverteilung ist hinsichtlich des Mittelwertes, des Modalwertes und des Medians (die bei μ jeweils gleich sind) symmetrisch.
Häufig werden mit Binomial- und Poisson-Verteilungen diskrete, voneinander unabhängige, zufällige, wahre oder falsche Ereignisse in der Zukunft (zum Beispiel die Häufigkeit, mit der beim Werfen einer Münze "Kopf" fällt) mit einer relativ kleinen Anzahl von Beobachtungen modelliert, während mit der Normalverteilung kontinuierliche Variablen (z. B. Größe, Gewicht und Menge) mit einer großen Anzahl von Beobachtungen modelliert werden. Die Binomial- und Poisson-Verteilungen beruhen auf der Wahrscheinlichkeit, während die Normalverteilung die Anzahl der Beobachtungen darstellt, die mit der Menge oder Größe übereinstimmt.
Exponentialverteilung
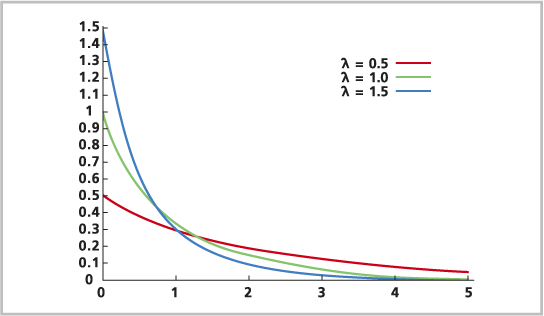
Die Exponentialverteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung. Sie wird im Allgemeinen zum Modellieren der Zeit zwischen Ereignissen verwendet, die mit einer konstanten Durchschnittsrate auftreten. Die Verteilung kann aber auch zum Modellieren der Häufigkeit von Ereignissen in einer Distanz pro Einheit verwendet werden. Exponentialverteilungen können beispielsweise für die Zeit bis zum nächsten Verkehrsunfall auf einer Kreuzung, die Zeit zwischen der Beobachtung zweier Sternschnuppen am Nachthimmel und für den Abstand zwischen Schlaglöchern auf einer Straße verwendet werden. Bei jedem dieser Beispiele nimmt mit zunehmender Zeit oder Entfernung die Wahrscheinlichkeit einer Zustandsänderung oder des Eintretens des Ereignisses exponentiell zu. Die Vorkommen der Ereignisse sind voneinander unabhängig.
Für die Exponentialverteilung gilt die folgende Formel:
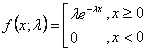
wobei
e ist der natürliche Logarithmus.
x ist die mögliche Häufigkeit für das Ereignis (positive Ganzzahlwerte).
Mit der Exponentialverteilung werden Poisson-Prozesse modelliert, bei denen sich das Phänomen im Ausgangszustand befindet. Die Exponentialverteilung ist die kontinuierliche Version der geometrischen Verteilung. Wenn der Prozess des Wechsels von Zustand A in Zustand B in mehrere voneinander unabhängige Tasks unterteilt werden kann, sollte dieser besser mit einer Gamma-Verteilung modelliert werden. Mit der Gamma-Verteilung wird die Summe mehrerer voneinander unabhängiger, exponentiell verteilter Variablen modelliert. Die Gamma-Verteilung kann als Sonderfall der Exponentialverteilung angesehen werden.
Poisson-Verteilung
Die Poisson-Verteilung ist eine diskrete Wahrscheinlichkeitsverteilung. Mit der Poisson-Verteilung wird die Wahrscheinlichkeit der Häufigkeit von Ereignissen in einem festen Zeitraum bei einem bekannten Mittelwert modelliert. Die Ereignisse sind von ihrem jeweils letzten Eintreten unabhängig. Auf der X-Achse sind die diskreten Werte für die Ereignisse 0, 1, 2, 3, 4 usw. abgetragen (die meist die Häufigkeit des Ereignisse darstellen), und die Y-Achse entspricht der Wahrscheinlichkeit, mit der das Phänomen bei einem bekannten Mittelwert mit der entsprechenden Häufigkeit eintritt. Als Ereignisse können die Anzahl der Unfälle auf einer Kreuzung, die Anzahl von Geburtsfehlern oder die Anzahl von Hirschen pro Quadratkilometer verwendet werden. Mit der Poisson-Verteilung werden seltene Ereignisse modelliert. Die Verteilung wird manchmal als "Gesetz der kleinen Zahlen" bezeichnet, da das Ereignis zwar nicht häufig eintritt, jedoch viele Möglichkeiten für das Eintreten vorhanden sind.
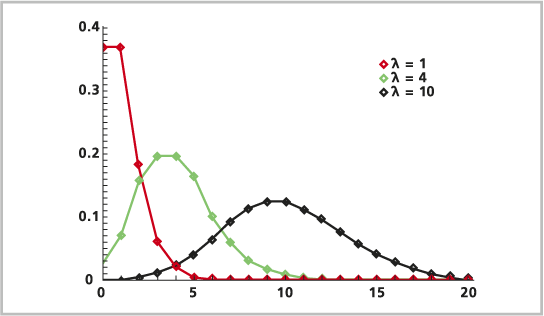
Die Formel ist unten angegeben:
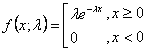
wobei
e ist der natürliche Logarithmus.
k ist die mögliche Häufigkeit für das Ereignis (positive Ganzzahlwerte).
k! ist eine Fakultät von k.
λ (oder der Mittelwert) ist eine positive Zahl, die die erwartete Häufigkeit innerhalb eines bestimmten Intervalls darstellt. Wenn das Ereignis alle 10 Minuten eintritt, beträgt der Lambda-Wert für eine Stunde (60 Minuten) 6.
Die Poisson-Verteilung ähnelt der Binomialverteilung. Mit der Poisson-Verteilung wird jedoch die Häufigkeit eines seltenen Ereignisses modelliert, ohne dass Informationen zur möglichen Gesamthäufigkeit bekannt sind. Mit der Poisson-Verteilung wird die Anzahl der Unfälle auf einer Kreuzung untersucht, während mit der Binomialverteilung die Anzahl der Unfälle im Verhältnis zur Anzahl der die Kreuzung passierenden Autos modelliert wird.
Gamma-Verteilung
Die Gamma-Verteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung. Mit der Gamma-Verteilung wird die Summe mehrerer voneinander unabhängiger, exponentiell verteilter Variablen modelliert. Die Gamma-Verteilung kann als Sonderfall der Exponentialverteilung angesehen werden.
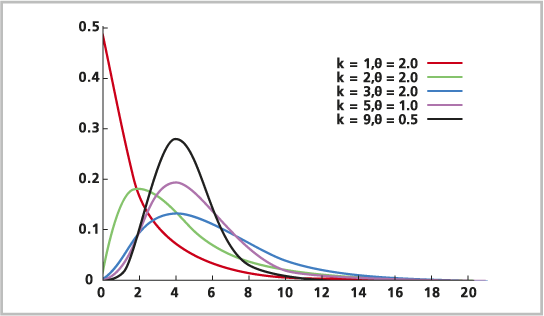
Für die Gamma-Verteilung gilt die folgende Formel:
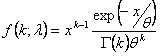
Die Gamma-Verteilung kann auch folgendermaßen parametrisiert werden:
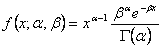
Beim Alpha-Wert 1 gleicht die Gamma-Verteilung der Exponentialverteilung. Wenn der Alpha-Wert ein Ganzzahl-Wert ist, wird die Gamma-Verteilung zur Erlang-Verteilung. Bei einem Alpha-Ganzzahlwert und einem Beta-Wert von 2 wird die Gamma-Verteilung zu einer Chi-Quadrat-Verteilung mit 2 Freiheitsgraden für Alpha.
Die sich ergebenden Variablen sind größer oder gleich 0,0. Alpha und Beta müssen größer als 0,0 sein.
Binomialverteilung
Mit der Binomialverteilung wird die Häufigkeit eines Ereignisses bei Beobachtung einer Folge potenzieller Verursacher des Ereignisses modelliert. Beispielsweise kann mit der Binomialverteilung die Anzahl von Menschen in einer medizinischen Untersuchung erfasst werden, die an Herzkrankheiten gestorben sind, sowie die Anzahl der Personen, die auf der zweiten Etage aus einem vollen Fahrstuhl aussteigen, oder auch die Anzahl der Tiere in einer Population, die ein bestimmtes genetisches Merkmal tragen.
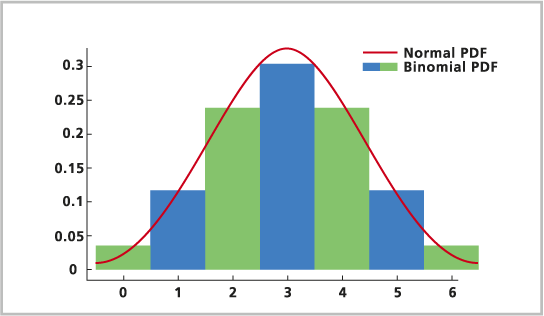
Mit der Binomialverteilung werden Vorkommen beschrieben, keine Größen. Es kann modelliert werden, wie viele Teilnehmer ein Rennen beendet haben, nicht aber, wie schnell die Teilnehmer waren.
Für die Binomialverteilung gilt die folgende Formel:
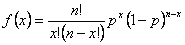
wobei
n ist die Anzahl der Beobachtungen.
p ist die Wahrscheinlichkeit des Vorkommens.
x ist die Anzahl der Erfolge von 0 bis n.
Ein gängiges Beispiel für die Verwendung der Binomialverteilung ist die Wahrscheinlichkeitsermittlung für die Häufigkeit, mit der bei 10 Münzwürfen (n = 10) "Kopf" fällt. "Kopf" kann in 0 von 10 Fällen, 1 von 10 Fällen usw. fallen, daher x = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. p ist die Wahrscheinlichkeit für jeden Wert x.
Alle Versuche sind voneinander unabhängig, und jeder Versuch führt zum Ergebnis Erfolg oder Misserfolg.
Die Binomialverteilung nähert sich bei einem großen Wert für n und einem kleinen Wert für p der Poisson-Verteilung an. In diesem Fall ist die Poisson-Verteilung möglicherweise leichter zu verwenden.
Die Binomialverteilung gibt eine Zufallsvariable für die Anzahl von Erfolgen aus n Versuchen zurück, wobei die Wahrscheinlichkeit für den Erfolg pro Versuch gleich p ist (z. B. ist die Wahrscheinlichkeit von "Kopf" beim Münzwurf gleich p).
Geometrische Verteilung
Die geometrische Verteilung ist eine diskrete Wahrscheinlichkeitsverteilung. Zwei Typen von Phänomenen werden mit dieser Verteilung hauptsächlich modelliert: (1) die Wahrscheinlichkeit einer Anzahl von Versuchen bis zu einem Erfolg (z. B. die Anzahl der Versuche beim Würfeln, bis eine 6 fällt), oder (2) die Wahrscheinlichkeit einer Anzahl von erfolglosen Versuchen, bevor ein Erfolg erzielt wird (z. B. die Anzahl der Wanderungen auf einem bestimmten Pfad, bevor ein Hirsch gesehen wird). Die Wahrscheinlichkeit, auf der ersten Wanderung keinen Hirsch zu sehen, liegt bei (1 - p). Auf der zweiten Wanderung liegt die Wahrscheinlichkeit, keinen Hirsch zu sehen, bei (1 - p) (1 - p). Bei weiteren Wanderungen auf dem Pfad nimmt die Wahrscheinlichkeit, keinen Hirsch zu sehen, exponentiell ab, und letztlich tritt dieses Ereignis ein. Die Ereignisse sind voneinander unabhängig.
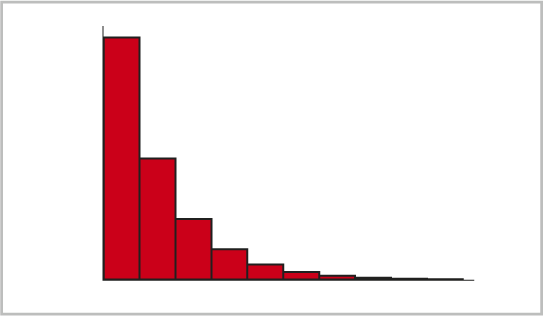
Für die geometrische Verteilung gilt die folgende Formel:

wobei
p ist die Wahrscheinlichkeit eines Erfolgs.
n ist die Anzahl der Versuche.
Die geometrische Verteilung ist die diskrete Version der Exponentialverteilung (siehe oben). Die geometrische Verteilung ist ein Sonderfall der negativen Binomial- oder Pascal-Verteilung, wobei r in der Pascal-Verteilung gleich 1 ist (siehe unten).
Negative Binomialverteilung
Die negative Binomialverteilung ist eine diskrete Wahrscheinlichkeitsverteilung. Diese Verteilung basiert auf Bernoulli-Versuchen. Mit Bernoulli-Versuchen werden Ereignisse modelliert, bei denen Versuche zu einem von zwei Ergebnissen führen können (Erfolg oder Misserfolg), eine Erfolgswahrscheinlichkeit p aufweisen (wobei p für jeden Versuch gleich ist) und voneinander unabhängig sind. Der Wurf einer Münze stellt einen Bernoulli-Versuch dar. Mit der negativen Binomialverteilung kann z. B. modelliert werden, wie viele Münzwürfe benötigt werden, bis fünfmal nacheinander "Kopf" fällt. Daher wird mit der negativen Binomialverteilung die Anzahl von Misserfolgen vor einem Erfolg modelliert. Wenn r ein Ganzzahl-Wert ist, wird die negative Binomialverteilung zu einem Sonderfall, der als Pascal-Verteilung bezeichnet wird.
Für die negative Binomialverteilung gilt die folgende Formel:
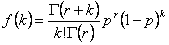
wobei
r ist die Anzahl der Misserfolge.
p ist die Wahrscheinlichkeit eines Erfolgs.
k ist die Anzahl der Erfolge von 0 bis n.
Wenn die negative Binomialverteilung das Werfen einer Münze darstellt, wird für die Anzahl von Versuchen, bis "Kopf" fällt, ein zufälliger Wert zurückgegeben.