Wenn Sie das Werkzeug Regressionsanalyse ausführen, erhalten Sie als primäre Ausgabe einen Bericht. Bei der Ausführung im Vordergrund wird der Bericht im Fenster mit den Geoverarbeitungsmeldungen angezeigt, Sie können jedoch auch im Fenster Ergebnisse darauf zugreifen. Darüber hinaus kann optional auch eine Tabelle erstellt werden, mit der Sie die getesteten Modelle ausführlicher untersuchen können. Der Zweck des Berichts besteht zum einen darin herauszufinden, ob die von Ihnen in Betracht gezogenen potenziellen erklärenden Variablen zu ordnungsgemäß spezifizierten OLS-Modellen führen. Falls es keine bestandenen Modelle geben sollte (Modelle, die alle beim Starten des Werkzeugs Regressionsanalyse angegebenen Kriterien erfüllen), gibt die Ausgabe jedoch auch an, welche Variablen zuverlässige Prädiktoren sind, und unterstützt Sie dabei zu ermitteln, welche Diagnosen zu Problemen führen. Strategien zum Beheben von Problemen mit den einzelnen Diagnoseprogrammen finden Sie im Dokument Grundlagen zur Regressionsanalyse (siehe Allgemeine Regressionsprobleme, Folgen und Lösungen) und unter Was Sie noch nicht über die Regressionsanalyse wussten. Weitere Informationen darüber, wie Sie ermitteln können, ob Ihr Modell ein ordnungsgemäß spezifiziertes OLS-Modell ist, finden Sie unter Grundlagen zur Regressionsanalyse und Interpretieren von OLS-Ergebnissen.
Der Bericht
Der Bericht Regressionsanalyse hat fünf verschiedene Abschnitte. Die einzelnen Abschnitte werden nachfolgend beschrieben.
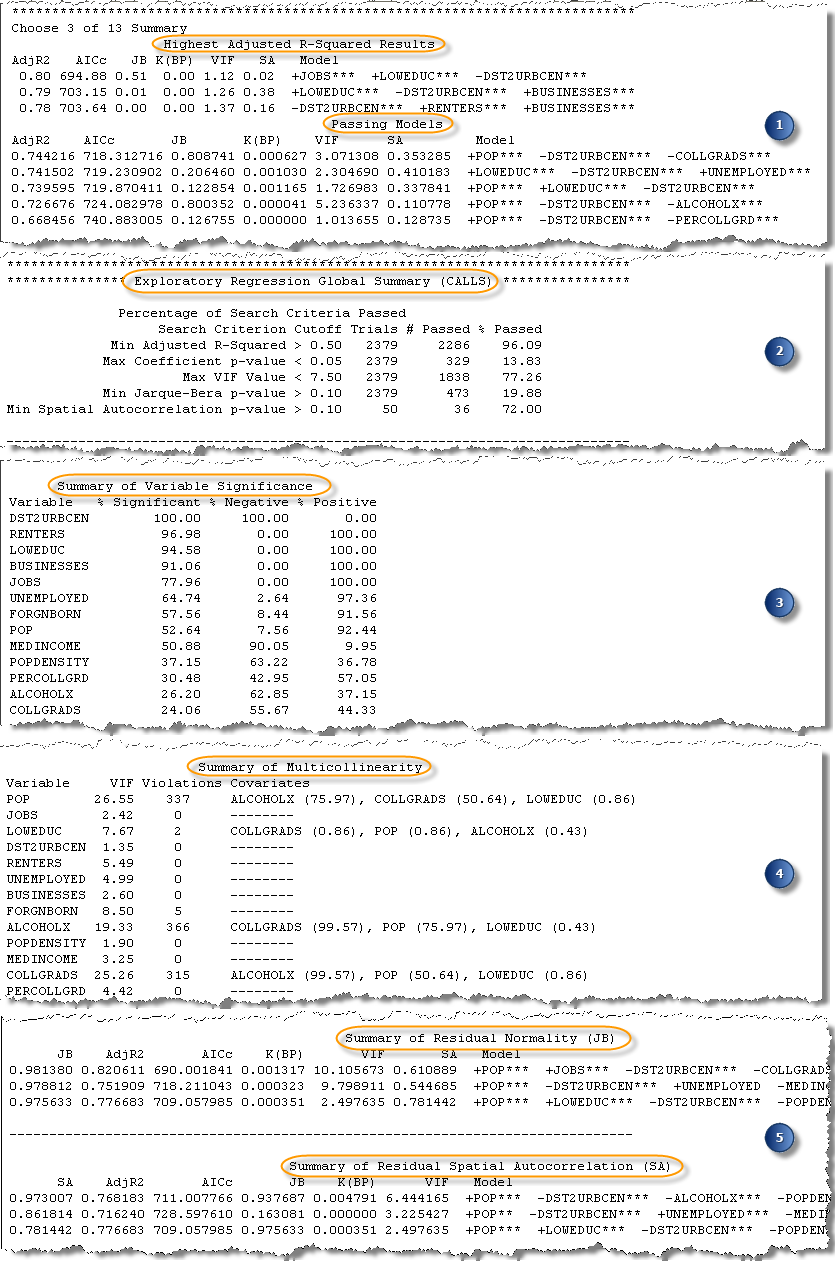
1. Beste Modelle nach Anzahl der erklärenden Variablen
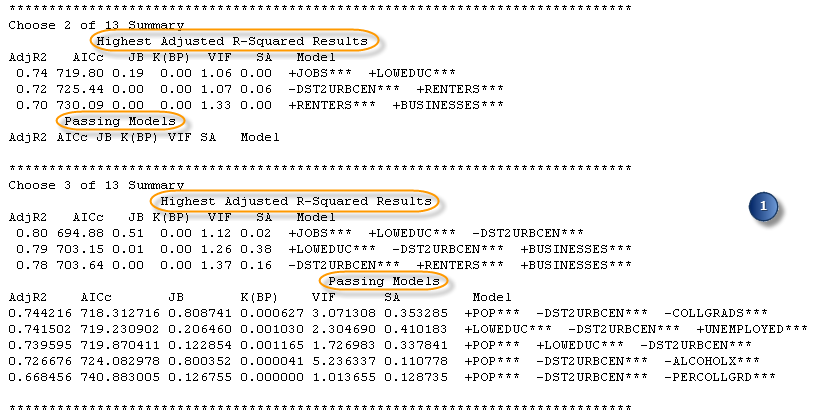
Die ersten Zusammenfassungen im Ausgabebericht sind nach der Anzahl der erklärenden Variablen in den getesteten Modellen gruppiert. Wenn Sie für den Parameter Minimale Anzahl erklärender Variablen 1 angeben und für den Parameter Maximale Anzahl erklärender Variablen 5, werden fünf zusammenfassende Abschnitte aufgeführt. In jedem Abschnitt sind die drei Modelle mit den höchsten Werten für Adjusted R2 sowie alle bestandenen Modelle aufgeführt. Jeder zusammenfassende Abschnitt umfasst auch die Diagnosewerte für jedes aufgelistete Modell: korrigiertes Akaike's Information Criterion - AICc, Jarque-Bera-p-Wert - JB, Koenkers t-verteilter Breusch-Pagan-p-Wert - K(BP), den größten Variance Inflation Factor - VIF und einen Messwert der residualen räumlichen Autokorrelation (Globaler p-Wert von Morans I) - SA. Mithilfe dieser Zusammenfassung erhalten Sie einen Überblick darüber, wie gut die Vorhersagen Ihrer Modelle sind (Adj R2) und ob Modelle alle der von Ihnen angegebenen Diagnosekriterien erfüllen. Wenn Sie alle standardmäßigen Suchkriterien übernommen haben (Parameter Minimaler annehmbarer Adj R-Squared, Maximaler p-Wert für Koeffizient - Grenzwert, Maximaler VIF-Wert - Grenzwert, Minimaler annehmbarer p-Wert Jarque Bera und Minimaler annehmbarer p-Wert für räumliche Autokorrelation), sind alle Modelle in der Liste Bestandene Modelle ordnungsgemäß spezifizierte OLS-Modelle.
Wenn keine bestandenen Modelle vorhanden sind, finden Sie im restlichen Teil des Ausgabeberichtes trotzdem nützliche Informationen über die Variablenbeziehungen, und er kann Sie bei der Entscheidung zur weiteren Vorgehensweise unterstützen.
2. Globale Zusammenfassung der Regressionsanalyse
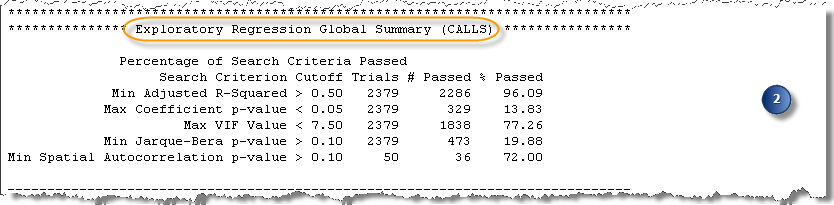
Der Abschnitt Globale Zusammenfassung der Regressionsanalyse ist insbesondere dann ein wichtiger Ausgangspunkt, wenn keine bestandenen Modelle gefunden wurden, da in diesem Abschnitt deutlich wird, warum keine der Modelle bestanden haben. In diesem Abschnitt sind die fünf Diagnosetests und der Prozentsatz der Modelle aufgeführt, die die einzelnen Tests bestanden haben. Wenn keine bestandenen Modelle ermittelt werden konnten, können Sie mithilfe dieser Zusammenfassung ermitteln, bei welchem Diagnosetest es zu Problemen kommt.
Der Diagnosetest, der am häufigsten Probleme verursacht, ist der Global Moran’s I-Test für die räumliche Autokorrelation (SA). Wenn alle getesteten Modelle über räumlich autokorrelierte Regressionsresiduen verfügen, weist dies häufig darauf hin, dass wichtige erklärende Variablen fehlen. Eine der besten Möglichkeiten, um fehlende erklärende Variablen zu ermitteln, besteht darin, die Karte der Residuen zu untersuchen, die vom OLS-Regressionswerkzeug (Ordinary Least Squares, kleinste Quadrate) ausgegeben wird. Wählen Sie eines der untersuchenden Regressionsmodelle aus, die für alle anderen Kriterien gute Ergebnisse erzielt haben (anhand der Liste der höchsten Adjusted R-Squared-Werte oder durch Auswahl eines Modells in der optionalen Ausgabetabelle), und führen Sie die OLS mit diesem Modell aus. Die Ausgabe des OLS-Regressionswerkzeugs ist eine Karte der Modell-Residuen. Sie sollten die Residuen untersuchen, da sie möglicherweise Hinweise darauf geben, was fehlt. Versuchen Sie, so viele potenzielle räumliche Variablen wie möglich zu identifizieren (beispielsweise die Entfernung zu wichtigen Fernstraßen, zu Krankenhäusern oder anderen wichtigen geographischen Features). Ziehen Sie die Verwendung von Variablen der räumlichen Ordnung in Betracht: Wenn alle zu niedrigen Vorhersagen beispielsweise in ländlichen Gebieten auftreten, erstellen Sie eine Dummy-Variable, um zu ermitteln, ob sich hierdurch die Ergebnisse der untersuchenden Regression verbessern.
Ein weiterer Diagnosetest, der häufig Probleme verursacht, ist der Jarque-Bera-Test für normal verteilte Residuen. Wenn keines Ihrer Modelle den Jarque-Bera-Test (JB) besteht, liegt eine Modellverzerrung vor. Zu den häufigen Ursachen für eine Modellverzerrung zählen unter anderem:
- Nicht lineare Beziehungen
- Datenausreißer
Durch die Anzeige einer Scatterplotmatrix der potenziellen erklärenden Variablen in Bezug auf die abhängige Variable können Sie ermitteln, ob eines dieser Probleme vorliegt. Weitere Strategien werden unter Grundlagen zur Regressionsanalyse erläutert. Wenn die Modelle beim räumlichen Autokorrelationstest (SA) Fehler aufweisen, beheben Sie diese zuerst. Die Verzerrung kann darauf zurückzuführen sein, dass wichtige erklärende Variablen fehlen.
3. Zusammenfassung der Variablensignifikanz
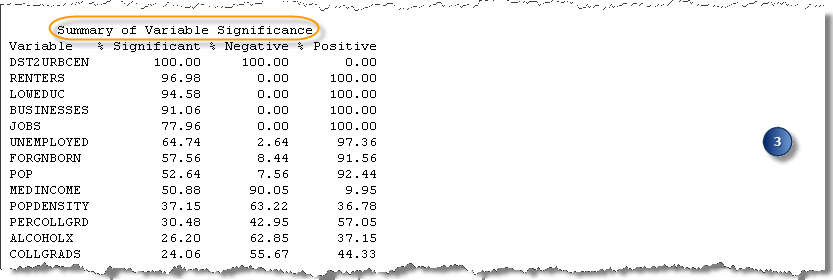
Der Abschnitt Zusammenfassung der Variablensignifikanz enthält Informationen über Variablenbeziehungen und die Zuverlässigkeit dieser Beziehungen. Jede potenzielle erklärende Variable wird mit der proportionalen Häufigkeit, wie oft sie statistisch signifikant war, aufgeführt. Die ersten Variablen in der Liste weisen die höchsten Werte in der Spalte % Signifikant auf. Anhand der Spalten % Negativ und % Positiv können Sie ebenfalls erkennen, wie stabil die Variablenbeziehungen sind. Starke Prädiktoren sind zuverlässig signifikant (% Signifikant), und die Beziehung ist stabil (primär negativ oder primär positiv).
Dieser Teil des Berichtes zielt außerdem darauf ab, Ihre Effizienz zu steigern. Dies ist insbesondere dann wichtig, wenn Sie mit sehr vielen (mehr als 50) potenziellen erklärenden Variablen arbeiten und Modelle mit fünf oder mehr Prädiktoren ausprobieren möchten. Wenn Sie sehr viele erklärende Variablen verwenden und zahlreiche Kombinationen testen möchten, kann die Berechnung sehr viel Zeit in Anspruch nehmen. In einigen Fällen kann es tatsächlich vorkommen, dass das Werkzeug aufgrund von ausgelastetem Arbeitsspeicher die Berechnungen nicht abschließen kann. Eine empfehlenswerte Herangehensweise ist es, die Anzahl der getesteten Modelle Schritt für Schritt zu erhöhen: Beginnen Sie, indem Sie für die Parameter Minimale Anzahl erklärender Variablen und Maximale Anzahl erklärender Variablen zunächst 2, dann 3, dann 4 usw. festlegen. Entfernen Sie bei jedem Ausführen die Variablen, die in den getesteten Modellen kaum statistisch relevant sind. Anhand des Abschnitts Zusammenfassung der Variablensignifikanz können Sie die Variablen ermitteln, die zuverlässig starke Prädiktoren sind. Selbst wenn Sie nur eine potenzielle erklärende Variable aus der Liste entfernen, kann dies die Verarbeitungsdauer des Werkzeugs Regressionsanalyse deutlich verringern.
4. Zusammenfassung der Multikollinearität
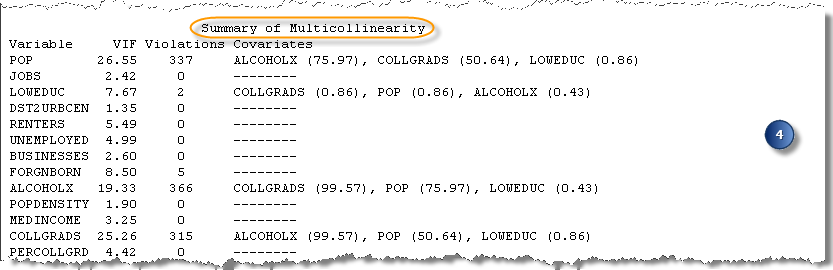
Sie können den Abschnitt Zusammenfassung der Multikollinearität des Berichts zusammen mit dem Abschnitt Zusammenfassung der Variablensignifikanz verwenden, um zu ermitteln, welche potenziellen erklärenden Variablen aus der Analyse entfernt werden können, um die Performance zu steigern. Im Abschnitt Zusammenfassung der Multikollinearität erfahren Sie, wie oft jede erklärende Variable in einem Modell mit Multikollinearität einbezogen wurde. Außerdem werden hier die anderen in diesen Modellen enthaltenen erklärenden Variablen aufgeführt. Wenn zwei (oder mehr) erklärende Variablen häufig zusammen in Modellen mit hoher Multikollinearität gefunden werden, weist dies darauf hin, dass diese Variablen wahrscheinlich das gleiche aussagen. Da Sie jedoch nur Variablen einbeziehen möchten, die eindeutige Aspekte der abhängigen Variablen erläutern, sollten Sie nur eine der redundanten Variablen in weiteren Analysevorgängen einschließen. Hierzu können Sie basierend auf der Zusammenfassung der Variablensignifikanz die stärkste der redundanten Variablen auswählen.
5. Weitere Diagnosezusammenfassungen

Die letzten Diagnosezusammenfassungen zeigen die höchsten Jarque-Bera-p-Werte (Zusammenfassung der residualen Normalität) und die höchsten globalen p-Werte für Moran’s I (Zusammenfassung der residualen räumlichen Autokorrelation). Um diese Diagnosetests zu bestehen, benötigen Sie große p-Werte.
Diese Zusammenfassungen sind nicht besonders nützlich, wenn Ihre Modelle den Jarque-Bera-Test und räumlichen Autokorrelationstest (Global Moran’s I) bestehen. Wenn Ihr Kriterium für die statistische Signifikanz 0,1 beträgt, sind alle Modelle mit höheren Werten als 0,1 gleichsam bestandene Modelle. Diese Zusammenfassungen sind jedoch nützlich, wenn keine bestandenen Modelle vorhanden sind und Sie ermitteln möchten, wie weit Sie von normal verteilten Residuen entfernt sind oder welche Residuen keine statistisch signifikante räumliche Autokorrelation aufweisen. Wenn zum Beispiel alle p-Werte für die Jarque-Bera-Zusammenfassung 0,000000 lauten, ist eindeutig, dass Sie weit von normal verteilten Residuen entfernt sind. Wenn die p-Werte jedoch 0,092 lauten, wissen Sie, dass Sie kurz davor sind, normal verteilte Residuen zu erhalten (tatsächlich kann ein p-Wert von 0,092 auch als bestanden gelten, abhängig von der Signifikanzstufe). Diese Zusammenfassungen dienen dazu, die Schwere des Problems zu verdeutlichen, und wenn keine Modelle bestehen, welche Variablen mit den Modellen verknüpft sind, die zumindest kurz davor sind zu bestehen.
Die Tabelle
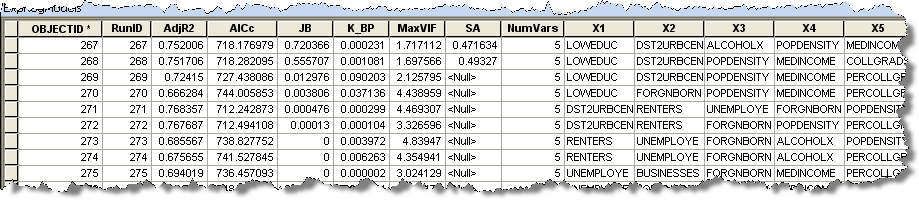
Wenn Sie für die Ausgabeergebnistabelle einen Wert angegeben haben, wird eine Tabelle mit all den Modellen erstellt, die die Kriterien für Maximaler p-Wert für Koeffizient - Grenzwert und Maximaler VIF-Wert - Grenzwert erfüllen. Auch wenn keine bestandenen Modelle vorhanden sind, sind in der Regel einige Modelle in der Ausgabetabelle aufgeführt. Jede Zeile in der Tabelle entspricht einem Modell, das die Kriterien für die Koeffizienten- und VIF-Werte erfüllt. In den Tabellenspalten sind die Modelldiagnosen und die erklärenden Variablen aufgeführt. Die aufgelisteten Diagnosen sind Adjusted R-Squared (R2), korrigiertes Akaike's Information Criterion (AICc), Jarque-Bera-p-Wert (JB), Koenkers t-verteilter Breusch-Pagan-p-Wert (BP), Variance Inflation Factor (VIF) und globaler p-Wert von Moran’s I (SA). Sie können die Modelle zum Beispiel nach den AICc-Werten sortieren. Je niedriger der AICc-Wert ist, desto besser die Leistung des Modells. Sie können die AICc-Werte in ArcMap sortieren, indem Sie auf die AICc-Spalte doppelklicken. Wenn Sie ein Modell zur Verwendung in einer OLS-Analyse auswählen (um die Residuen zu untersuchen), wählen Sie ein Modell mit einem niedrigen AICc-Wert und bestandenen Werten für so viele andere Diagnosetest wie möglich aus. Wenn Sie zum Beispiel den Ausgabebericht genau untersucht haben und wissen, dass die Probleme vor allem mit dem Jarque-Bera-Test auftraten, verwenden Sie das Modell mit dem niedrigsten AICc-Wert, das alle Kriterien außer für Jarque-Bera erfüllt hat.
Zusätzliche Quellen
Wenn Sie mit der Regressionsanalyse in ArcGIS noch nicht vertraut sind, empfehlen wir Ihnen dringend, das kostenlose Esri Virtual Campus Training Seminar zur Regression anzusehen und dann das Lernprogramm für Regressionsanalysen durchzuarbeiten, bevor Sie die Regressionsanalyse verwenden.
Nachfolgend finden Sie weitere nützliche Quellen:
- Weitere Informationen zur Regressionsanalyse
- Was Sie noch nicht über die Regressionsanalyse wussten
- Grundlagen zur Regressionsanalyse
Burnham, K.P. and D.R. Anderson. 2002. Model Selection and Multimodel Inference: a practical information-theoretic approach, 2nd Edition. New York: Springer. Section 1.5.
Auf der Seite Spatial Statistics Resources finden Sie außerdem ständig neue Videos, Lernprogramme und andere Schulungsmaterialien.