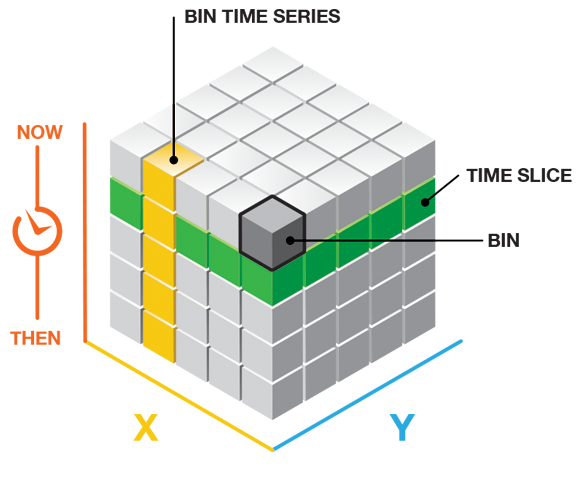
Mit dem Werkzeug Raum-Zeit-Würfel durch Aggregieren von Punkten erstellen werden mit einem Zeitstempel versehene Punkt-Features mittels Aggregation der Punkte zu Raum-Zeit-Abschnitten in einen netCDF-Datenwürfel strukturiert. Alle in einem Abschnitt enthaltenen Punkte werden gezählt, jede Zusammenfassungsfeld-Statistik wird berechnet, und mithilfe der Mann-Kendall-Statistik wird der Trend für die Abschnitte im Zeitverlauf für jede Position ermittelt. Dieses Werkzeug dient in erster Linie zur Erstellung eines Eingabe-Würfels für anschließendes Raum-Zeit-Muster-Mining , man kann damit aber auch Zeitserientrends im Untersuchungsgebiet analysieren.
Interpretieren von Ergebnissen
Das Werkzeug gibt eine netCDF-Repräsentation Ihrer Eingabe-Punkte aus. Die Würfelpunktanzahl kann in ArcGIS Pro in 2D oder 3D visualisiert werden. Zusätzlich zur netCDF-Datei werden im Ergebnisfenster Meldungen angezeigt, die eine Zusammenfassung der Raum-Zeit-Würfel-Dimensionen und -Inhalte enthalten. Wenn Sie auf den Eintrag Meldungen im Ergebnisfenster klicken und Anzeigen wählen, werden die Ergebnisse in einem Meldungsdialogfeld angezeigt.

Die Struktur des Würfels umfasst Zeilen, Spalten und Zeitschritte. Multipliziert man die Anzahl der Zeilen mit der Anzahl der Spalten und der Anzahl der Zeitschritte, erhält man die Gesamtanzahl der Abschnitte des Würfels. Mit den Zeilen und Spalten wird die räumliche Ausdehnung und mit den Zeitschritten die zeitliche Ausdehnung des Würfels bestimmt.
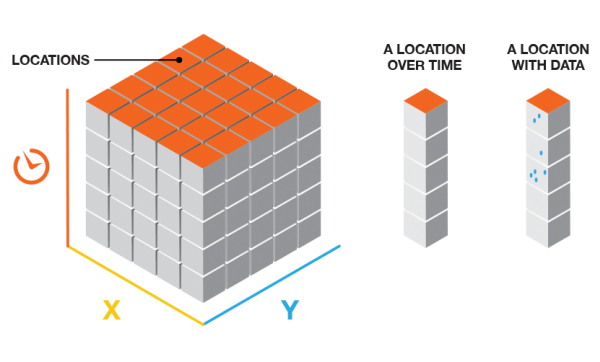
In den meisten Analysen werden lediglich Positionen mit Daten für mindestens ein Zeitintervall berücksichtigt, sie werden jedoch über alle Zeitschritte hinweg analysiert. Beim Berechnen der Punktanzahl werden Punktzahlen von Null angenommen für Abschnitte, die keine Punkte enthalten, deren zugeordnete Position jedoch bei mindestens einem Zeitintervall mindestens einen Punkt aufzuweisen hatte. Angaben zum prozentualen Anteil von Nullen, die Positionen zugeordnet sind, die für mindestens ein Zeitintervall Daten enthalten, werden in den Meldungen als "geringe Dichte" angegeben. Beim Berechnen der Werte für Zusammenfassungsfelder bestimmt der Parameter Leere Abschnitte füllen mit, wie Abschnitte, die keine Punkte aufweisen, gefüllt werden. Alle Abschnitte, die nicht basierend auf den Schätzungskriterien gefüllt werden können, führen dazu, dass die gesamte Position aus der Analyse ausgeschlossen wird. Zum Füllen leerer Abschnitte mit dem Durchschnittswert räumlicher Nachbarn sind mindestens 4 räumliche Nachbarn und zum Füllen leerer Abschnitte mit dem Durchschnittswert von Raum-Zeit-Nachbarn sind mindestens 13 Nachbarn erforderlich.
Am Ende der Ausgabe-Meldung sind Angaben zum "Datentrend Gesamt" vorhanden. Dieser Trend basiert auf der Analyse einer lageunabhängigen Zeitserie. Diese beantwortet allgemein die Frage, ob die von den Eingabepunkten repräsentierten Ereignisse im Zeitverlauf zunehmen oder abnehmen. Zur Beantwortung dieser Frage wird die Anzahl der Punkte für alle Positionen in jedem Zeitintervall in Form einer Zeitserie von Anzahlwerten mithilfe der Mann-Kendall-Statistik analysiert.
Abschnittsbemaßungen zur Aggregation
In den meisten Fällen wissen Sie, wie die Dimensionen der Würfelabschnitte festzulegen sind, und es empfiehlt sich, genauestens darüber nachzudenken, welche Dimensionen für die Beantwortung der jeweiligen Fragestellung geeignet sein könnten. Wenn Sie Verbrechen untersuchen, könnten Sie beispielsweise Punkte in 400-m-Abschnitte aggregieren, da dies in etwa einer Straßenlänge in einem Stadtviertel entspricht. Wenn Ihnen die Daten eines ganzen Jahres vorliegen, könnten Sie Trends untersuchen, deren Ereignisse monatlich oder wöchentlich zusammengefasst wurden.
Standardparameter
Sollten Sie, was nur selten der Fall sein dürfte, kein bestimmtes Zeitintervall oder Abstandsintervall bevorzugen, dann können Sie die Parameter Zeitintervall oder Entfernungsintervall unausgefüllt und das Werkzeug die Werte für Sie berechnen lassen.
Die Standard-Abschnittsentfernung wird wie folgt berechnet:
- Bestimmen Sie die Entfernung der längsten Seite der Ausdehnung der Eingabe-Features (maximale Ausdehnung).
- Die Abschnittsentfernung ist dann der größere Wert der maximalen Ausdehnung dividiert durch 100 oder einem Algorithmus, der auf der räumlichen Verteilung der Eingabe-Features basiert.
Das Standard-Zeitintervall basiert auf zwei verschiedenen Algorithmen, die zur Ermittlung der optimalen Anzahl und Weite der Zeitintervalle verwendet werden. Das geringere numerische Ergebnis aus diesen Algorithmen, größer als 10, wird als Standard-Anzahl für diese Zeitintervalle herangezogen. Sind beide numerischen Ergebnisse kleiner als 10, wird 10 als Standardwert für Zeitintervalle festgelegt.
Zeitschrittausrichtung
Die Zeitschrittausrichtung ist ein wichtiger Parameter, der beim Aggregieren der Daten in einem Raum-Zeit-Würfel berücksichtigt werden muss, da er den Beginn und das Ende der Aggregation bestimmt. Hier ein Beispiel zur Verdeutlichung:
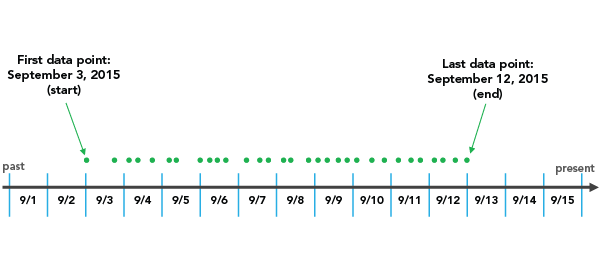
Endzeit
Wenn beispielsweise eine END_TIME Zeitschrittausrichtung mit einem Zeitschrittintervall von 3 Tagen ausgewählt wird, startet die Klasseneinteilung mit dem letzten Datenpunkt und geht in Schritten von 3 Tagen zurück, bis alle Daten in einen Zeitschritt fallen.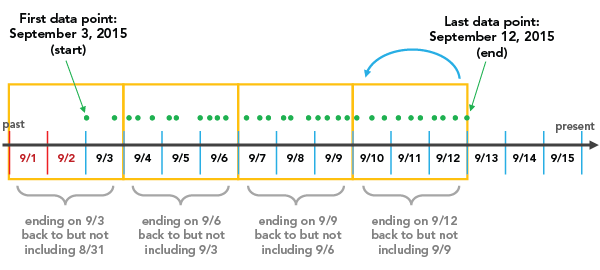
Hierbei ist zu beachten, dass es je nach ausgewähltem Zeitintervall möglich ist, einen Zeitschritt am Anfang des Raum-Zeit-Würfels zu erstellen, der im gesamten Zeitraum keine Daten aufweist. Dem Beispiel oben ist zu entnehmen, dass 9/1 und 9/2 im ersten Zeitschritt enthalten sind, obwohl bis 9/3 keine Daten vorhanden sind. Diese leeren Tage sind Teil des Zeitschritts, sie sind jedoch mit keinen Daten verknüpft. Dadurch können Ihre Ergebnisse verzerrt werden, da der vorübergehend verzerrte Zeitschritt deutlich weniger Punkte aufzuweisen scheint als andere Zeitschritte, was tatsächlich ein künstliches Ergebnis des Aggregationsschemas ist. Der Bericht gibt an, ob eine zeitliche Verzerrung im ersten oder letzten Zeitschritt vorhanden ist. In diesem Fall weisen 2 von 3 Tagen im ersten Zeitschritt keine Daten auf, sodass die zeitliche Verzerrung 66 % beträgt.
END_TIME ist die Standardoption für Zeitschrittausrichtung , da viele Analysen auf die letzten Vorgänge fokussiert sind, sodass eine Verzerrung in Richtung Beginn des Würfels vorzuziehen ist. Eine andere Lösung ohne zeitliche Verzerrung ist die Bereitstellung von Daten, die gleichmäßig auf das Zeitintervall verteilt sind, sodass keine Zeiträume verzerrt sind. Hierzu können Sie einen Auswahlsatz der Daten erstellen, die den Teil des Punkt-Datasets ausschließen, der sich außerhalb des Zeitraums befindet, den Sie als ersten Zeitraum festlegen möchten. In diesem Beispiel kann das Problem gelöst werden, indem alle Daten, ausgenommen die Daten vor 9/4, ausgewählt werden. Der Bericht zeigt die Zeitspanne des ersten und letzten Zeitschritts an, und anhand dieser Informationen kann ermittelt werden, wo die Trennung erfolgen muss.
Wenn der Start des letzten Abschnitts beim zeitlichen Zurückgehen zufällig genau auf den ersten Datenpunkt fällt, muss außerdem beachtet werden, dass der letzte Datenpunkt nicht in diesen Abschnitt einbezogen wird. Dies ist darauf zurückzuführen, dass bei einer END_TIME Zeitschrittausrichtung jeder Abschnitt das letzte Datum in einem angegebenen Abschnitt enthält, zum ersten Datum in diesem Abschnitt zurückkehrt, dieses aber nicht in diesen Abschnitt einbezieht. In diesem Fall muss daher ein zusätzlicher Abschnitt hinzugefügt werden, um sicherzustellen, dass der erste Datenpunkt einbezogen wird.
Startzeit
Wenn beispielsweise eine START_TIME Zeitschrittausrichtung mit einem Zeitschrittintervall von 3 Tagen ausgewählt wird, startet die Klasseneinteilung mit dem ersten Datenpunkt und geht in Schritten von 3 Tagen nach vorn, bis das letzte Datum in den letzten Zeitschritt fällt.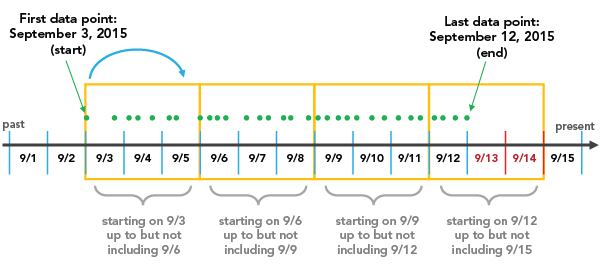
Es müssen einige wichtige Punkte berücksichtigt werden. Ein Punkt ist, dass es bei einer START_TIME Zeitschrittausrichtung je nach ausgewähltem Zeitschrittintervall möglich ist, einen Zeitschritt am Ende des Raum-Zeit-Würfels zu erstellen, der im gesamten Zeitraum keine Daten aufweist. Dem Beispiel oben ist zu entnehmen, dass 9/13 und 9/14 im letzten Zeitschritt enthalten sind, obwohl nach 9/12 keine Daten vorhanden sind. Diese leeren Tage sind Teil des Zeitschritts, sie sind jedoch mit keinen Daten verknüpft. Dadurch können Ihre Ergebnisse verzerrt werden, da der vorübergehend verzerrte Zeitschritt deutlich weniger Punkte aufzuweisen scheint als andere Zeitschritte, was tatsächlich ein künstliches Ergebnis des Aggregationsschemas ist. Der Bericht gibt an, ob eine zeitliche Verzerrung im ersten oder letzten Zeitschritt vorhanden ist. In diesem Fall weisen 2 von 3 Tagen im letzten Zeitschritt keine Daten auf, sodass die zeitliche Verzerrung 66 % beträgt. Dies ist besonders dann problematisch, wenn eine START_TIME Zeitschrittausrichtung ausgewählt wird, da Analysen, die auf die aktuellen Daten fokussiert sind, deutlich beeinflusst werden können. Die Lösung besteht darin, Daten bereitzustellen, die gleichmäßig auf das Zeitintervall verteilt sind, sodass keine Zeiträume verzerrt sind. Hierzu können Sie einen Auswahlsatz der Daten erstellen und dieser schließt den Teil des Punkt-Datasets aus, der sich außerhalb des Zeitraums befindet, den Sie als letzten Zeitraum festlegen möchten. In diesem Beispiel kann das Problem gelöst werden, indem alle Daten, ausgenommen die Daten nach 9/11, ausgewählt werden. Sie können auch zwei Tage vom Anfang des Datasets trennen, was ebenfalls dazu führen würde, dass das Datum gleichmäßig in den Zeitschritte liegt. Der Bericht zeigt die Zeitspanne des ersten und letzten Zeitschritts an, und anhand dieser Informationen kann ermittelt werden, wo die Trennung erfolgen muss.
Wenn das Ende des letzten Zeitschritts beim zeitlichen Vorwärtsgehen zufällig genau auf den letzten Datenpunkt fällt, muss außerdem beachtet werden, dass der letzte Datenpunkt nicht in diesen Abschnitt einbezogen wird. Dies ist darauf zurückzuführen, dass bei einer START_TIME Zeitschrittausrichtung jeder Abschnitt das erste Datum in einem angegebenen Abschnitt enthält, zum letzten Datum in diesem Abschnitt vorwärts geht, dieses aber nicht in diesen Abschnitt einbezieht. In diesem Fall muss daher ein zusätzlicher Abschnitt hinzugefügt werden, um sicherzustellen, dass der letzte Datenpunkt einbezogen wird.
Bezugszeit
Mit einer REFERENCE_TIME Zeitschrittausrichtung können Sie sicherstellen, dass ein bestimmtes Datum den Anfang oder das Ende eines der Zeitschritte in dem Würfel kennzeichnet.
Wenn eine REFERENCE_TIME ausgewählt wird, die hinter der Ausdehnung des Datasets, auf dem letzten Datenpunkt oder in der Mitte des Datasets liegt, wird sie wie der letzte Punkt eines Zeitschritts behandelt und alle anderen Abschnitte auf beiden Seiten werden mit einer Zeitschrittausrichtung erstellt, bis alle Daten abgedeckt sind, wie unten dargestellt.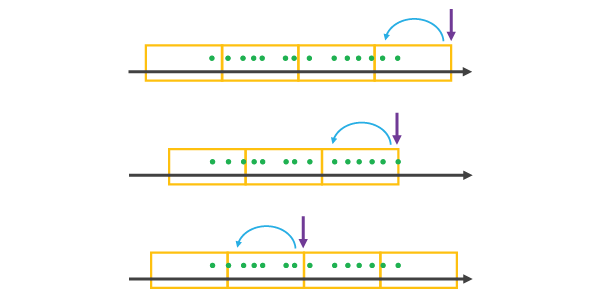
Wenn eine REFERENCE_TIME ausgewählt wird, die vor der Ausdehnung des Datasets oder auf dem ersten Datenpunkt liegt, wird sie wie der erste Datenpunkt eines Zeitschritts behandelt und alle anderen Zeitschritte auf beiden Seiten werden mit einer START_TIME Zeitschrittausrichtung erstellt, bis alle Daten abgedeckt sind, wie unten dargestellt.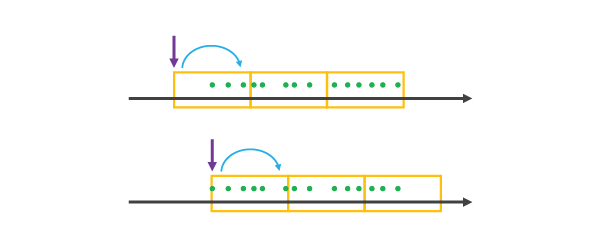
Beachten Sie, dass bei Auswahl einer REFERENCE_TIME vor oder nach der Ausdehnung Ihrer Daten möglicherweise leere oder teilweise leere Abschnitte erstellt werden, die Ihre Analyse verzerren.
Vorlagewürfel
Wenn Sie einen Vorlagewürfel auswählen, können Sie eine konsistente räumliche Ausdehnung und ein Zeitintervall auswählen, während Sie andere Datasets analysieren. Sie können beispielsweise den Raum-Zeit-Würfel des letzten Jahres als Vorlagewürfel verwenden, nachdem die Daten des nächsten Jahres abgerufen wurden, weil dadurch die Konsistenz in der verwendeten räumlichen Ausdehnung und dem Zeitschrittintervall sichergestellt wird, wodurch die Ausdehnung des Würfels die neuen Daten abdecken kann. Sie haben auch die Möglichkeit, den Raum-Zeit-Würfel für einen Ereignistyp als Vorlagewürfel für die Analyse eines anderen Ereignistyps heranzuziehen, um sicherzustellen, dass ein Vergleich der Analyseergebnisse gültig ist.
Die Auswahl eines Vorlagewürfels hat Auswirkungen auf die Zeitschrittausrichtung. Hier einige Beispiele: Wenn Sie einen Vorlagewürfel auswählen, der vor oder nach der Zeitspanne der Eingabe-Features liegt, werden Zeitschritte hinzugefügt, bis alle Daten durch einen Zeitschritt abgedeckt sind, indem die Zeitschrittausrichtung des
Vorlagewürfels verwendet wird. Der resultierende Raum-Zeit-Würfel weist leere Würfel dort auf, wo der Vorlagewürfel die Eingabe-Features nicht zeitlich überlappt. Dadurch können die Ergebnisse einer Analyse verzerrt werden. Wenn der Vorlagewürfeldie Eingabe-Features überlappt, deckt der Raum-Zeit-Würfel die zeitliche Ausdehnung des Vorlagewürfels ab und dehnt sich aus, bis alle Eingabe-Features abgedeckt sind. Dazu wird die Zeitschrittausrichtung des
Vorlagewürfels verwendet. In der Abbildung unten sind Vorlagewürfel blau und die resultierenden Raum-Zeit-Würfel orangefarben dargestellt.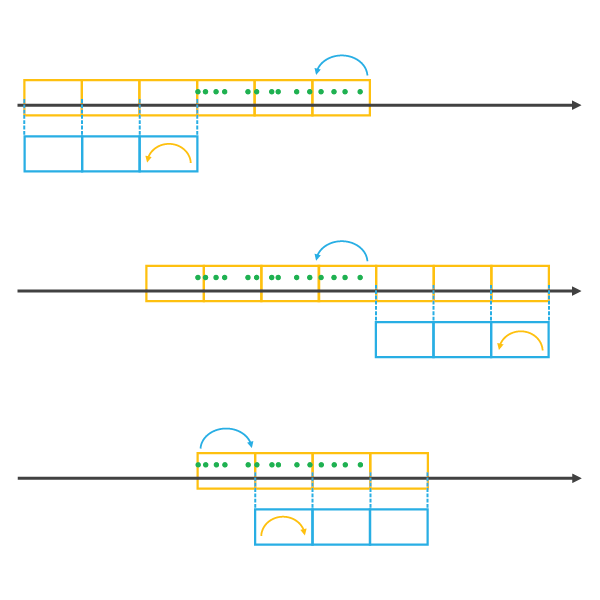
Hierbei ist zu beachten, dass beim Erstellen eines neuen Raum-Zeit-Würfels mit einem Vorlagewürfel die zeitliche Ausdehnung des Vorlagewürfels ausgedehnt wird, bis alle Daten abgedeckt sind. Dadurch können Sie anhand des Würfels des letzten Jahres einen neuen Würfel erstellen, der sowohl die Daten des letzten als auch die dieses Jahres enthält. Die räumliche Ausdehnung des Vorlagewürfels wird anders behandelt. Alle Daten, die außerhalb der räumlichen Ausdehnung des Vorlagewürfels liegen, werden aus der Analyse ausgeschlossen. Der Vorlagewürfel und der resultierende Raum-Zeit-Würfel weisen identische räumliche Ausdehnungen auf. Änderungen können nur in der räumlichen Ausdehnung vorkommen, in der Positionen, die zuvor keine Daten aufwiesen, zu Positionen mit Daten werden können, wenn neue Features aufgetreten sind, die nicht vorhanden waren als der Vorlagewürfel erstellt wurde.
Trendanalyse
Die Mann-Kendall-Trendanalyse kommt bei jeder Position, die Daten enthält, als Zeitserientest für unabhängige Abschnitte zum Einsatz. Die Mann-Kendall-Statistik stellt eine Rangstufenkorrelationsanalyse für die Abschnittszählung bzw. -werte und deren zeitliche Abfolge dar. Der Abschnittswert des ersten Zeitraums wird mit dem Abschnittswert des zweiten verglichen. Wenn der erste Wert kleiner ist als der zweite, wird als Ergebnis +1 ausgegeben. Ist der erste Wert größer als der zweite, lautet das Ergebnis -1. Sind beide Werte gleich groß, ist das Ergebnis 0. Die Ergebnisse für jedes verglichene Zeitraumpaar werden addiert. Die erwartete Summe beträgt 0, woraus hervorgeht, dass die Werte im zeitlichen Verlauf keinen Trend aufweisen. Auf der Grundlage der Varianz der Werte in der Abschnitts-Zeitserie, der Anzahl der Gleichstände und der Anzahl der Zeiträume wird die beobachtete Summe mit der erwarteten Summe (0) verglichen, um zu ermitteln, ob die Differenz statistisch signifikant ist oder nicht. Der Trend für jede Abschnitts-Zeitserie wird als Z-Score und p-Wert vermerkt. Ein kleiner p-Wert verweist darauf, dass der Trend statistisch signifikant ist. Das Vorzeichen des Z-Wertes lässt erkennen, ob der Trend eine Zunahme (positiver Z-Wert) oder Abnahme (negativer Z-Wert) der Abschnittswerte darstellt. Strategien zur Visualisierung der Trendergebnisse werden unter Raum-Zeit-Würfel visualisieren beschrieben.
Zusätzliche Quellen
Bei der Erstellung, Visualisierung und Analyse des Raum-Zeit-Würfels wird die von UCAR/Unidata entwickelte netCDF-Software verwendet. Weitere Informationen zu Unidata und dem NetCDF (Network Common Data Form)-Projekt finden Sie hier.
Optimierung der Abschnittsbreite in Histogrammen
- Shimazaki H. und Shinomoto S., A method for selecting the bin size of a time histogram in Neural Computation (2007) Bd. 19(6), 1503–1527.
- Terrell, G. and Scott, D., Oversmoothed Nonparametric Density Estimates. Journal of the American Statistical Association (1985) Vol. 80(389), 209-214.
- Online-Statistik-Lernprogramm: Ein Multimedia-Kurs (http://onlinestatbook.com/). Projektleiter: David M. Lane, Rice University (Kapitel 2, "Graphing Distributions, Histograms" [Diagrammverteilungen, Histogramme]).
Mann-Kendall-Trendanalyse
- Hamed, K. H., Exact distribution of the Mann-Kendall trend test statistic for persistent data, in Journal of Hydrology (2009), 86–94.
- Kendall, M. G., Gibbons, J. D., Rank correlation methods, 5. Aufl., (1990) Griffin, London.
- Mann, H. B., Nonparametric tests against trend in Econometrica (1945) Bd. 13, 245–259.