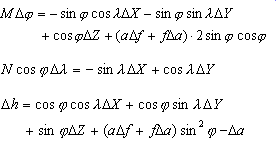Gleichungsbasierte Transformationsmethoden können in die folgenden vier Methodentypen unterteilt werden.
Methoden mit drei Parametern
Die einfachste Datumstransformationsmethode ist eine geozentrische Transformation bzw. eine Transformation mit drei Parametern. Bei der geozentrischen Transformation werden die Unterschiede zwischen zwei Datumsangaben im XYZ- oder kartesischen 3D-Koordinatensystem modelliert. Ein Datum wird mit dem Mittelpunkt 0,0,0 definiert. Der Mittelpunkt des anderen Datums ist in einer Entfernung (dx,dy,dz oder ΔX,ΔY,ΔZ) in Metern definiert.
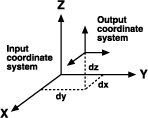
Normalerweise werden die Transformationsparameter so definiert, dass der Ausgangspunkt ein lokales Datum und das Ziel das World Geodetic System (WGS) von 1984 oder ein anderes geozentrisches Datum ist.
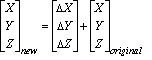
Die drei Parameter sind lineare Verlagerungen, und die Maßeinheit ist immer Meter.
Methoden mit sieben Parametern
Eine komplexere und genauere Datumstransformation ist möglich, indem einer geozentrischen Transformation vier weitere Parameter hinzugefügt werden. Die sieben Parameter sind drei lineare Verlagerungen (dx,dy,dz), drei Winkeldrehungen um die einzelnen Achsen (rx,ry,rz) und ein Skalierungsfaktor.
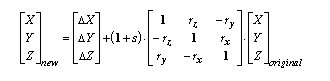
Die Drehwerte sind in Dezimalsekunden angegeben, der Skalierungsfaktor in Teilen pro Million (parts per million, ppm). Die Drehwerte werden auf zwei unterschiedliche Arten definiert: als positiv im Uhrzeigersinn oder gegen den Uhrzeigersinn, je nach Blickrichtung auf den Ursprung der XYZ-Systeme.
Die obige Gleichung stellt dar, wie die Vereinigten Staaten und Australien die Gleichungen definieren. Sie wird als Coordinate-Frame-Rotation-Transformation bezeichnet. Die Drehungen sind positiv gegen den Uhrzeigersinn. In Europa wird eine andere Konvention, die Positionsvektor-Transformation, verwendet. Beide Methoden werden manchmal als Bursa-Wolf-Methode bezeichnet. In der Projection Engine sind die Coordinate-Frame- und die Bursa-Wolf-Methode identisch. Die Coordinate-Frame- und die Positionsvektor-Methode werden beide unterstützt, und Transformationswerte können leicht von einer Methode in die andere konvertiert werden, indem einfach die Vorzeichen der drei Drehwerte geändert werden. Beispiel: Die Parameter, die mit der Coordinate-Frame-Methode aus dem Datum WGS 1972 in das Datum WGS 1984 konvertiert werden sollen, sind (in der Reihenfolge dx,dy,dz,rx,ry,rz,s):
(0.0, 0.0, 4.5, 0.0, 0.0, -0.554, 0.227)Um die gleichen Parameter mit der Positionsvektor-Methode zu verwenden, ändern Sie das Vorzeichen der Drehung, sodass dies die neuen Parameter sind:
(0.0, 0.0, 4.5, 0.0, 0.0, +0.554, 0.227)Nur anhand der Parameter kann die verwendete Konvention nicht abgeleitet werden. Wenn Sie die falsche Methode einsetzen, können Ihre Ergebnisse ungenaue Koordinaten enthalten. Die einzige Möglichkeit, die Art der Definition der Parameter zu bestimmen, ist die Prüfung eines Passpunktes, dessen Koordinaten in den beiden Systemen bekannt sind.
Die Molodensky-Badekas-Methode ist eine Variation der Methoden mit sieben Parametern. Sie weist zusätzlich drei Parameter auf, die den XYZ-Ursprung der Drehung definieren. Manchmal wird dieser Punkt als Ursprung des Datums oder des geographischen Koordinatensystems bezeichnet. Wenn der XYZ-Ursprung des Drehpunkts bekannt ist, kann eine entsprechende Coordinate-Frame-Transformation berechnet werden. Die dx-, dy- und dz-Werte ändern sich, aber die Dreh- und Skalenwerte bleiben gleich.
Molodensky-Methode
Bei der Molodensky-Methode erfolgt die Konvertierung direkt zwischen zwei geographischen Koordinatensystemen ohne eine Konvertierung in ein XYZ-System. Die Molodensky-Methode erfordert drei Verlagerungen (dx,dy,dz) sowie die Unterschiede zwischen den großen Halbachsen (Δa) und den Abplattungen (Δf) der zwei Sphäroide. Die Projection Engine berechnet die Sphäroidunterschiede automatisch gemäß den beteiligten Datumsangaben.
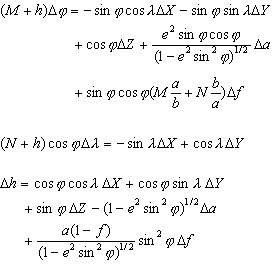
- h = Ellipsoidhöhe (Meter)
- Φ = Breitengrad
- λ = Längengrad
- a = große Halbachse des Sphäroids (Meter)
- b = kleine Halbachse des Sphäroids (Meter)
- f = Abplattung des Sphäroids
- e = Exzentrizität des Sphäroids
M und N sind der meridionale bzw. der erste vertikale Radius der Krümmung bei einem bestimmten Breitengrad. Die Gleichungen für M und N lauten:
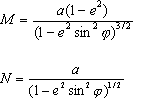
Sie berechnen nach Δλ und ΔΦ. Die Beträge werden von der Projection Engine automatisch addiert.
Vereinfachte Molodensky-Methode
Die vereinfachte Molodensky-Methode ist eine einfachere Version der Molodensky-Methode. Siehe folgende Gleichungen: