Bei Transformationen werden Daten innerhalb eines Koordinatensystems verschoben. Sie werden häufig verwendet, um Daten von unbekannten Digitalisierungsgeräten oder Scanner-Einheiten in reale Koordinaten zu konvertieren. Transformationen können auch verwendet werden, um Einheiten innerhalb eines Koordinatensystems zu konvertieren, wie zum Beispiel Fuß in Meter. Um Daten zwischen Koordinatensystemen zu konvertieren, zum Beispiel geographisch in UTM, sollten Sie stattdessen die Daten projizieren.
Die Transformationsfunktionen basieren auf dem Vergleich der Koordinaten der Quell- und Zielpunkte, der so genannten Passpunkte, in speziellen Grafikelementen, die als Versatz-Links bezeichnet werden. Bei Transformationen werden die Quell- und Zielpositionen der Links verwendet, um die Transformationsformeln zu konstruieren. Diese Links können Sie interaktiv erstellen, indem Sie bekannte Quell- und Zielpositionen verwenden oder durch Laden einer Linktextdatei oder Passpunktedatei.
Beim Erstellen der Links für Transformationen versuchen Sie, dieselbe Position in den Quell- und Zielpositionen zu finden. Ein Beispiel sei ein Straßen-Layer, den Sie an die Position anderer Daten transformieren oder verschieben möchten, in denen eine Luftaufnahme enthalten sein kann. Wenn Sie Versatz-Links erstellen, könnte das Von-Ende an einer Kreuzung im Straßen-Layer platziert werden, während das Bis-Ende an der entsprechenden Kreuzung auf dem Bild platziert werden sollte. Links müssen nicht unbedingt in Features beginnen oder enden. Die Entfernung zwischen den Quell- und Zielpositionen kann häufig ziemlich groß sein.
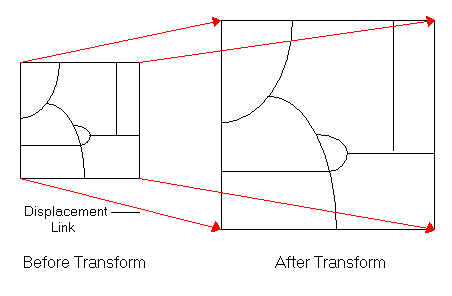
ArcMap unterstützt standardmäßig drei Typen der Transformation: Affin, Ähnlichkeit und Projektiv.
Affine Transformation
Bei einer affinen Transformation können die Daten unterschiedlich skaliert, verzerrt, gedreht und übertragen werden. In der folgenden Grafik sind die vier möglichen Änderungen dargestellt.
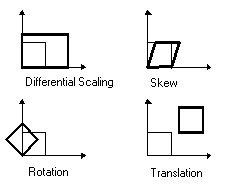
Die Funktion für die affine Transformation lautet
x’ = Ax + By + C y’ = Dx + Ey + F Dabei sind x und y die Koordinaten des Eingabe-Layers und x’ und y’ sind die transformierten Koordinaten. A, B, C, D, E und F werden durch Vergleich der Position der Quell- und Ziel-Passpunkte bestimmt. Mit ihnen werden die Layer-Koordinaten skaliert, gezerrt, gedreht und übertragen. Bei dieser Methode werden mindestens drei Links benötigt. Für die meisten Transformationen wird diese Methode empfohlen.
Für die affine Transformation werden mindestens drei Versatz-Links benötigt.
Ähnlichkeitstransformation
Mit der Ähnlichkeitstransformation werden die Daten skaliert, gedreht und übertragen. Weder werden die Achsen unabhängig skaliert noch wird eine Verzerrung vorgenommen. Das Seitenverhältnis der transformierten Features bleibt erhalten. Wichtig ist dies, wenn die relative Form der Features erhalten bleiben soll.
Die Funktion für die Ähnlichkeitstransformation lautet
x’ = Ax + By + C y’ = -Bx + Ay + Fwobei gilt:
A = s * cos t B = s * sin t C = translation in x direction F = translation in y direction und
s = scale change (same in x and y directions) t = rotation angle, measured counterclockwise from the x-axisFür die Ähnlichkeitstransformation werden mindestens zwei Versatz-Links benötigt. Allerdings sind zum Erzeugen eines RMS-Fehlers (Root Mean Square, quadratisches Mittel) mindestens drei Links erforderlich.
Projektive Transformation
Die projektive Transformation basiert auf einer komplexeren Formel, für die mindestens vier Versatz-Links erforderlich sind.
x’ = (Ax + By + C) / (Gx + Hy + 1) y’ = (Dx + Ey + F) / (Gx + Hy + 1) Diese Methode wird zum Transformieren von Daten verwendet, die direkt aus Luftaufnahmen erfasst werden. Weitere Informationen finden Sie in der Literatur zum Thema Photogrammetrie, die in den Hilfsreferenzen zur räumlichen Anpassung aufgeführt sind.
Restfehler und RMS-Fehler
Die Transformationsparameter stellen den bestmöglichen Kompromiss zwischen den Quell- und Ziel-Passpunkten dar. Wenn Sie mit den Transformationsparametern die tatsächlichen Passpunkte der Quelle transformieren, stimmen die transformierten Ausgabepositionen nicht mit den tatsächlichen Positionen der Ausgabe-Passpunkte überein. Dies wird als Restfehler bezeichnet. Er ist ein Maß für die Übereinstimmung der tatsächlichen Positionen mit den transformierten Positionen der Ausgabe-Passpunkte. Dieser Fehler wird für jeden Versatz-Link generiert.
Ein Root Mean Square-Fehler wird für jede ausgeführte Transformation berechnet. Er gibt an, wie gut die abgeleitete Transformation ist. Im folgenden Beispiel ist die relative Position von vier Ziel-Passpunkten und den transformierten Quell-Passpunkten dargestellt:
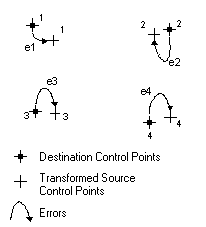
Der RMS-Fehler misst die Fehler zwischen den Ziel-Passpunkten und den transformierten Positionen der Quell-Passpunkte:
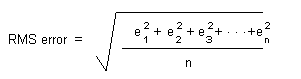
Die Transformation wird anhand der Methode der kleinsten Quadrate abgeleitet, sodass mehr Links als nötig angegeben werden können. Um eine Transformation zu erhalten, die einen RMS-Fehler generiert, müssen mindestens drei Links angegeben werden.
Generell gilt: Je mehr Links Sie für eine Transformation platzieren, desto genauer sind die Ergebnisse. Die Genauigkeit der Transformation können Sie überprüfen, indem Sie die RMS-Fehler in der Link-Tabelle anzeigen.
Blindtransformationen
Manchmal müssen Sie eine Anpassung, in der Regel eine Transformation, durchführen, bei der Sie keine Daten an der Zielposition haben und das Bis-Ende eines Versatz-Links nicht interaktiv platzieren können. Angenommen, Sie haben einige Daten digitalisiert und möchten sie von den Einheiten des Digitalisierungsgeräts in reale Koordinaten transformieren. In diesem Fall dürften Sie die realen Koordinaten einiger Feature-Positionen in Ihren Daten kennen, wie zum Beispiel eine Straßenkreuzung oder die Position eines Brunnens.
Sie können dann die Transformation einrichten, indem Sie Versatz-Links mit dem Von-Ende an bekannten Positionen und dem Bis-Ende an temporären Punkten im Raum erstellen. Danach können Sie die Link-Tabelle verwenden, um die Zielkoordinaten dieser Links so zu bearbeiten, dass sie an den entsprechenden realen Positionen liegen.