The Median Center tool is a measure of central tendency that is robust to outliers. It identifies the location that minimizes travel from it to all other features in the dataset. For example, if you were to compute the Mean Center for a compact cluster of points, the result would be a location at the center of the cluster. If you then added a new point far away from the cluster and recomputed the Mean Center, you would notice that the result would be pulled toward the new outlier. If you were to perform this same experiment using the Median Center tool, however, you would see that the new outlier has a much smaller impact on the result location. The Median Center tool allows you to specify a Weight Field. You can think of weights as the number of trips associated with each feature (for example, if the weight for a feature is 3.2, the number of trips would be 3.2). The weighted median center is the location that minimizes distance for all trips.
The method used to calculate the Median Center is an iterative procedure introduced by Kuhn and Kuenne (1962) and further outlined in Burt and Barber (1996). At each step (t) in the algorithm, a candidate Median Center is found (Xt, Yt) and then refined until it represents the location that minimizes the Euclidean Distance d to all features (or all weighted features) (i) in the dataset.
Calculations
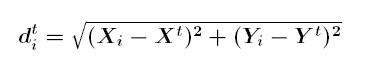
Output
The Median Center tool creates a new Output Feature Class with a single median center point feature, or single point feature for each case when a Case Field is specified. The X and Y median center values, case, and attribute field median values (one field for each Attribute Field specified) are attributes in the Output Feature Class. The value for each Attribute Field is the computed median for all the field values. The median for a set of numbers is the middle value: 1/2 of the values in the dataset are smaller, and 1/2 are larger.
Potential applications
You would use the Median Center tool when you want a measure of central tendency that is robust to spatial outliers. You might use it to compute the Median Center of fire activities when you don't want rare peripheral fire events to pull the result center location away from core fire activities. Often, it is interesting to compare Mean Center to Median Center results to see the impact peripheral features have on your result. For many applications, the Median Center is a more representative measure of central tendency than the Mean Center is.
Additional resources
The following references have further information about this tool:
Burt, J. E., and G. Barber. (1996). Elementary statistics for geographers. Guilford, New York.
Kuhn, H. W., and R. E. Kuenne (1962). An efficient algorithm for the numerical solution of the Generalized Weber Problem in spatial economics. Journal of Regional Science, 4(2):21–33.