 |
This document is archived and information here might be outdated. Recommended version. |
IAffineTransformation2D2.MoveOrigin Property (ArcObjects .NET 10.8 SDK)
|
This document is archived and information here might be outdated. Recommended version. |
The origin of accumulated transformations used when projecting an affine transformation to a different spatial reference system.
[Visual Basic .NET] Public ReadOnly Property MoveOrigin_2 As IPoint
[C#] public IPoint MoveOrigin_2 {get;}
[C++]
HRESULT get_MoveOrigin(
IPoint** Origin
);
[C++] Parameters Origin [out, retval]
Origin is a parameter of type IPoint**
Projecting a distance from one spatial reference to another is meaningless without specifying where the distance is measured. A line that is one unit in length in one spatial reference can map to a varying number of units on another spatial reference depending upon the location of the end points. For this reason, when your AffineTransformation2D has a translation (i.e., a Move), it is important to specify a point as the Origin for this move. This is done using the MoveOrigin property.
When the AffineTransformation2D you are projecting has a rotation, specifying a MoveOrigin is not necessary as the origin (or center) of the rotation is considered to be the origin of any translations as well.
Using a MoveOrigin that is closest to the geometry that you are projecting results in a more accurate transformation. In the following illustration, a point P1 is transformed by an AffineTransformation2D to the point P2. Both P1 and the Affine Transformation have the same spatial reference. P2 when projected to another spatial reference results in PP2.
If you project P1 and the Affine Transformation into PP2's spatial reference, and transform the projected point PP1 using the projected transformation, you will get the point PP2 provided you set the MoveOrigin of the AffineTransformation to P1 before projecting it. The results of this transformation will be more accurate when the MoveOrigin is closer to P1.
For the code illustrating this, see the example for this topic.
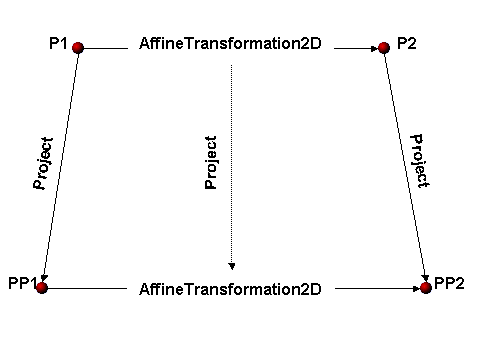
For an AffineTransformation2D to be projected, its MoveOrigin should be set so that it is within the horizons of the new projection.