IEllipticArc.PutCoordsByAngle Method

Sets the center point, starting angle, signed central angle, angle of rotation, ratio of the minor axis to the major axis, and axes.

[Visual Basic .NET]
Public Sub PutCoordsByAngle ( _
    ByVal ellipseStd As Boolean, _
    ByVal Center As IPoint, _
    ByVal FromAngle As Double, _
    ByVal CentralAngle As Double, _
    ByVal rotationAngle As Double, _
    ByVal semiMajor As Double, _
    ByVal minorMajorRatio As Double _
)

[C#]
public void PutCoordsByAngle (
    bool ellipseStd,
    IPoint Center,
    double FromAngle,
    double CentralAngle,
    double rotationAngle,
    double semiMajor,
    double minorMajorRatio
);

[C++]
HRESULT PutCoordsByAngle(
  VARIANT_BOOL ellipseStd,
  IPoint* Center,
  double FromAngle,
  double CentralAngle,
  double rotationAngle,
  double semiMajor,
  double minorMajorRatio
);

[C++]
Parameters
ellipseStd 

  ellipseStd is a parameter of type bool
Center 

  Center is a parameter of type IPoint*
FromAngle 

  FromAngle is a parameter of type double
CentralAngle 

  CentralAngle is a parameter of type double
rotationAngle 

  rotationAngle is a parameter of type double
semiMajor 

  semiMajor is a parameter of type double
minorMajorRatio 

  minorMajorRatio is a parameter of type double

Product Availability

Description

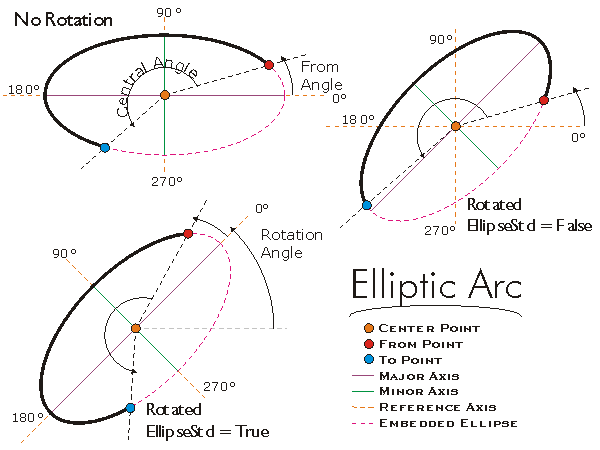
Creates an Elliptic Arc given the EllipseStd value, Center Point, From Angle, Central Angle, Rotation Angle, semi-Major Axis length, and Minor Axis to Major Axis Ratio.  If EllipseStd = TRUE, the From Angle is relative to the rotated semi-Major Axis rather than the X-Axis.

Remarks

This is the recommended way to create an arbitrary Elliptic Arc.  However, due to numeric accuracy limitations of computers and trigonometric functions, the From and To Points may be very slightly offset from the expected coordinates.  This is important to keep in mind when attempting to connect the endpoints to other segments.

See Also

IEllipticArc Interface | IEllipticArc.QueryCoordsByAngle Method