La agregación de datos de puntos de incidentes en cuadrículas con formas regulares se usa por muchas razones, como normalizar la geografía para la representación cartográfica o mitigar los problemas de usar polígonos irregulares creados arbitrariamente (como límites de condados o grupos de bloques que se hayan creado para un proceso político). Las cuadrículas de formas irregulares solo se pueden componer de triángulos equiláteros, cuadrados o hexágonos, ya que estas tres formas poligonales son las únicas que se pueden teselar (generar repitiendo la misma forma una y otra vez de borde a borde hasta cubrir un área sin huecos ni superposiciones) para crear una cuadrícula con un espaciado uniforme.

Aunque la cuadrícula cuadrada (red) es el tipo de forma más utilizada en el análisis SIG y la representación cartográfica temática, hay ocasiones en las que los hexágonos resultan más adecuados para el análisis dependiendo de la naturaleza de la pregunta formulada.
Los motivos para valorar la agregación en una cuadrícula hexagonal son los siguientes:
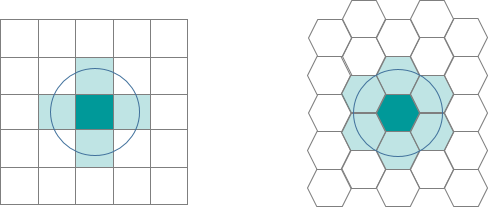
- Los hexágonos reducen el sesgo del muestreo debido a los efectos de borde de la forma de la cuadrícula, algo relacionado con la baja proporción entre perímetro y área de la forma del hexágono. Un círculo tiene la proporción más baja, pero no se puede teselar para formar una cuadrícula continua. Los hexágonos son los polígonos con la forma más circular que se pueden teselar para formar una cuadrícula con espaciado uniforme.
- Esta circularidad de una cuadrícula hexagonal permite representar las curvas de los patrones de los datos de un modo más natural que en las cuadrículas cuadradas.
- Cuando se comparan polígonos con áreas iguales, cuanto más similar a un círculo es el polígono, más cerca del centroide estarán los puntos cercanos al borde (especialmente los puntos cercanos a los vértices). Esto significa que cualquier punto situado dentro de un hexágono está más cerca del centroide del hexágono de lo que lo estaría un punto en un cuadrado o un triángulo equivalente (esto se debe a que los ángulos del cuadrado y el triángulo son más agudos que los del hexágono).
- Los hexágonos son preferibles cuando el análisis incluye aspectos relacionados con la conectividad o las rutas de movimiento.
- Debido a la naturaleza lineal de los rectángulos, las cuadrículas de red pueden guiar nuestra mirada por las líneas rectas paralelas ininterrumpidas, lo que puede inhibir los patrones subyacentes de los datos. Los hexágonos tienden a romper las líneas y permiten ver de una forma más clara y sencilla cualquier curvatura de los patrones de los datos. Esta rotura de los patrones lineales artificiales también reduce cualquier sesgo de la orientación que se pueda percibir en las cuadrículas de red.
- Si está trabajando en un área más grande, una cuadrícula hexagonal sufrirá menos distorsión a causa de la curvatura de la Tierra que la forma de una cuadrícula de red.
- Buscar vecinos es más sencillo con una cuadrícula hexagonal. Como el borde o la longitud de contacto son los mismos en cada lado, el centroide de cada vecino es equidistante. Sin embargo, con una cuadrícula de red, los centroides de los vecinos del Caso de la Reina (arriba/abajo/derecha/izquierda) están a N unidades de distancia, mientras que los centroides de los vecinos de la diagonal (Rook) están más lejos (exactamente a la raíz cuadrada de 2 x N unidades).
- Dado que la distancia entre los centroides es la misma en las seis direcciones para los hexágonos, si usa una banda de distancia para buscar los vecinos o usa las herramientas Análisis de puntos calientes optimizado, Análisis optimizado de valores atípicos o Crear cubo de espacio-tiempo agregando puntos, tendrá más vecinos incluidos en los cálculos de cada entidad si usa una cuadrícula hexagonal en lugar de una de red.
Recursos adicionales:
Birch, Colin P.D., Oom, Sander P. y Beecham, Jonathan A. Rectangular and hexagonal grids used for observation, experiment, and simulation in ecology. Ecological Modelling, Vol. 206, N.º 3–4. (agosto de 2007), pp. 347–359.