Funciones del descriptor de acceso espacial para ST_Geometry

Las funciones del descriptor de acceso devuelven la propiedad de una geometría. Existen funciones del descriptor de acceso para determinar las siguientes propiedades de una entidad ST_Geometry:

Dimensionalidad

Las dimensiones de una geometría son las coordenadas mínimas (ninguna, x, y) requeridas para definir la extensión espacial de la geometría.

Una geometría puede tener una dimensión de 0, 1 ó 2.

Las dimensiones son las siguientes:

• 0: no tiene ni longitud ni área
• 1: tiene longitud (x o y)
• 2: contiene área (x, y)

Los subtipos punto y multipunto tienen una dimensión de 0. Los puntos representan entidades de dimensión cero que pueden moldearse con una sola coordenada, mientras que los multipuntos representan datos que deben moldearse con un clúster de coordenadas desconectadas.

Los subtipos de cadena de texto de línea y cadena de texto multilínea tienen una dimensión de 1. Almacenan entidades como segmentos de carreteras, ramificación de sistemas de ríos y cualquier otra entidad que sea lineal por naturaleza.

Los subtipos polígono y multipolígono tienen una dimensión de 2. Las masas forestales, parcelas, cuerpos de agua y otras entidades que tienen perímetros que encierran un área definida pueden renderizarse mediante el tipo de datos de polígono o multipolígono.

La dimensión es importante no sólo como propiedad del subtipo sino también para determinar la relación espacial de dos entidades. La dimensión de la entidad o entidades resultantes determina si la operación se realizó de manera correcta o no. Se examinan las dimensiones de las entidades para determinar cómo deben compararse.

Para evaluar la dimensión de una geometría, utilice la función ST_Dimension, la cual toma la entidad de ST_Geometry y devuelve su dimensión como un número entero. Consulte ST_Dimension para obtener la sintaxis y un ejemplo del uso de esta función.

Las coordenadas de una geometría también tienen dimensiones. Si una geometría tiene solamente coordenadas x e y, la dimensión de la coordenada es 2. Si una geometría tiene coordenadas x, y, y z, la dimensión de la coordenada es 3. Si una geometría tiene coordenadas x, y, z y m, la dimensión de la coordenada es 4.

Puede utilizar la función ST_CoordDim para determinar las dimensiones presentes en una geometría.

Coordenadas z

Algunas geometrías tienen una altitud o profundidad asociada: una tercera dimensión. Cada uno de los puntos que forman la geometría de una entidad pueden incluir una coordenada z opcional que representa una altitud o profundidad relativa a la superficie de la tierra.

La función de predicado ST_Is3D toma ST_Geometry y devuelve 1 (TRUE) si la función tiene coordenadas z y 0 (FALSE) si no las tiene.

Puede determinar la coordenada z de un punto con la función ST_Z.

La función ST_MaxZ devuelve la coordenada z máxima, y la función ST_MinZ devuelve la coordenada z mínima de una geometría.

Medidas

Las medidas son valores asignados a cada coordenada. Se usan para aplicaciones de referenciación lineal y segmentación dinámica. Por ejemplo, las ubicaciones de hitos a lo largo de una carretera pueden contener mediciones que indican su posición. El valor representa todo lo que se puede almacenar como un número de doble precisión.

La función de predicado ST_IsMeasured toma una geometría y devuelve 1 (TRUE) si contiene medidas y 0 (FALSE) si no las tiene. (Solo se usa con las implementaciones de Oracle y SQLite de ST_Geometry.)

Puede averiguar el valor de medición de un punto con la función ST_M.

Tipo de geometría

El tipo de geometría se refiere al tipo de entidad geométrica. Estas incluyen lo siguiente:

• Puntos y multipuntos
• Líneas y multilíneas
• Polígonos y multipolígonos

ST_Geometry es una superclase que puede almacenar varios subtipos. Para determinar a qué subtipo pertenece una geometría, utilice la función ST_GeometryType o ST_Entity (solo Oracle y SQLite).

Colección de puntos (vértice) y cantidad de puntos

Una geometría puede tener cero o más puntos. Una geometría se considera vacía si tiene cero puntos. El subtipo punto es la única geometría que está restringida a cero o un punto; todos los demás subtipos pueden tener cero o más.

ST_Point

Un ST_Point es una geometría de cero dimensión que ocupa una sola ubicación en un espacio de coordenadas. Un ST_Point que tiene un solo valor de coordenada x,y siempre es simple y tiene un límite NULL. ST_Point puede utilizarse para definir entidades, como pozos petroleros, hitos y sitios de recolección de muestras de agua.

Las funciones que operan solamente sobre los tipos de datos ST_Point incluyen lo siguiente:

• ST_X: devuelve el valor de una coordenada x del tipo de dato de punto como un número de doble precisión
• ST_Y: devuelve el valor de una coordenada y del tipo de dato de punto como un número de doble precisión
• ST_Z: devuelve el valor de una coordenada z del tipo de dato de punto como un número de doble precisión
• ST_M: devuelve el valor de una coordenada m del tipo de dato de punto como un número de doble precisión

ST_MultiPoint

Un ST_MultiPoint es un conjunto de ST_Points y, como sus elementos, tiene una dimensión 0. El tipo ST_MultiPoint es simple si ninguno de sus elementos ocupa el mismo espacio de coordenadas. El límite de un ST_MultiPoint es NULL. ST_MultiPoints pueden definir cosas como patrones de transmisión aérea e incidentes del brote de una enfermedad.

Longitud y área

La longitud y el área son características mensurables de geometrías. Las cadenas de texto de líneas y los elementos de las cadena de texto multilínea tienen una sola dimensión y poseen la característica de la longitud. Los polígonos y los elementos de los multipolígonos son superficies de dos dimensiones y, por consiguiente, tienen un área que puede medirse. Puede usar las funciones ST_Length y ST_Area para determinar estas propiedades. Las unidades de medida varían según cómo se almacenan los datos.

ST_LineString

Un ST_LineString es un objeto unidimensional almacenado como una secuencia de puntos que define una ruta interpolada lineal. El tipo ST_LineString es simple si no se interseca con el interior. Los extremos (el límite) de un tipo ST_LineString cerrado ocupan el mismo punto en el espacio. Un tipo ST_LineString es un anillo si es cerrado y simple. Al igual que otras propiedades inherentes de ST_Geometry de superclase, ST_LineStrings tiene longitud. ST_LineStrings a menudo se utilizan para definir entidades lineales como carreteras, ríos y líneas de alimentación.

Los extremos normalmente forman el límite de un tipo ST_LineString a menos que éste sea cerrado, en cuyo caso el límite es NULL. El interior de ST_LineString es una ruta conectada que está entre los extremos, a menos que esté cerrada y, en tal caso, el interior es continuo.

Las funciones que operan en ST_LineStrings incluyen lo siguiente:

• ST_StartPoint: devuelve el primer punto de un ST_LineString especificado
• ST_EndPoint: devuelve el último punto de un ST_LineString
• ST_PointN: toma un ST_LineString y un índice en un punto n y devuelve ese punto
• ST_Length: devuelve la longitud de un ST_LineString como un número de doble precisión
• ST_NumPoints: evalúa un ST_LineString y devuelve la cantidad de puntos en su secuencia como un número entero
• ST_IsRing: una función de predicado que devuelve 1 (TRUE) si el ST_LineString especificado es un anillo, y 0 (FALSE) si no lo es
• ST_IsClosed: una función de predicado que devuelve 1 (TRUE) si el ST_LineString especificado está cerrado, y 0 (FALSE) si no lo está

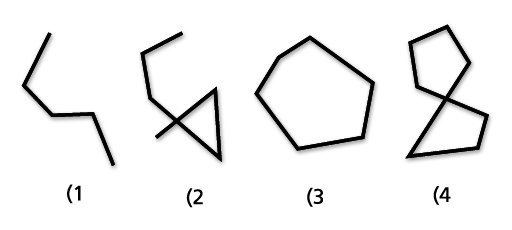
El gráfico siguiente muestra ejemplos de objetos ST_LineString: (1) es un ST_LineString simple y abierto; (2) es un ST_LineString que no es simple y está cerrado; (3) es un ST_LineString cerrado y simple y, por tanto, un anillo; y (4) es un ST_LineString cerrado que no es simple (no es un anillo).

ST_MultiLineString

Un ST_MultiLineString es una colección de ST_LineStrings. Los tipos ST_MultiLineStrings son simples si solo se intersecan en los extremos de los elementos de ST_LineString. Los tipos ST_MultiLineStrings no son simples si los interiores de los elementos de ST_LineString se intersecan.

El límite de un ST_MultiLineString son los extremos no intersecados de los elementos de ST_LineString. El límite de un ST_MultiLineString es NULL si todos los extremos de todos los elementos se intersecan. Además de las demás propiedades inherentes de ST_Geometry de superclase, ST_MultiLineStrings tiene longitud. ST_MultiLineStrings se usa para definir entidades lineales no contiguas, como arroyos o redes de carreteras.

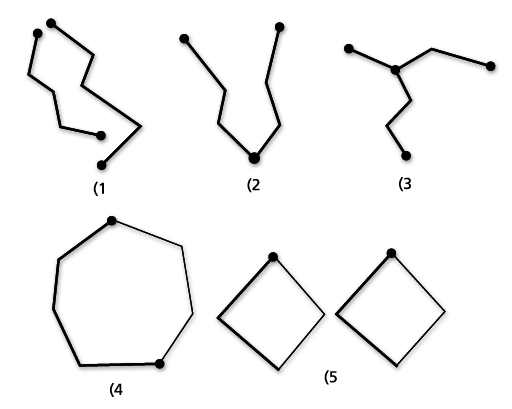
El siguiente gráfico proporciona ejemplos de ST_MultiLineStrings: (1) es un ST_MultiLineString simple para el cual el límite son los cuatro extremos de sus dos elementos ST_LineString. (2) es un ST_MultiLineString simple porque solo los extremos de los elementos de ST_LineString se intersecan. El límite consta de dos extremos que no se intersecan. (3) es un ST_MultiLineString no simple porque solo el interior de uno de sus elementos de ST_LineString se interseca. El límite de este ST_MultiLineString es cada uno de los tres extremos que no se intersecan. (4) es un ST_MultiLineString simple y abierto. No está cerrado porque su elemento ST_LineStrings no está cerrado. Es simple porque ninguno de los interiores de ninguno de los elementos de ST_LineStrings se intersecan. (5) es un ST_MultiLineString único, simple y abierto. Está cerrado porque todos sus elementos están cerrados. Es simple porque ninguno de sus elementos se interseca en los interiores.

Las funciones que operan en ST_MultiLineStrings incluyen ST_Length y ST_IsClosed.

La función ST_Length evalúa un ST_MultiLineString y devuelve la longitud acumulada de todos sus elementos ST_LineString como un número de doble precisión.

La función de predicado ST_IsClosed devuelve 1 (TRUE) si el ST_MultiLineString especificado está cerrado, y 0 (FALSE) si no lo está.

ST_Polygon

Un ST_Polygon es una superficie de dos dimensiones almacenada como una secuencia de puntos que define el anillo de delimitación exterior y 0 o más anillos interiores. Los ST_Polygons son siempre simples. Los ST_Polygons definen entidades que tienen una extensión espacial, como parcelas de tierra, cuerpos de agua y áreas de jurisdicción.

Este gráfico muestra ejemplos de objetos ST_Polygon: (1) es un ST_Polygon cuyo límite viene definido por un anillo exterior. (2) es un ST_Polygon cuyo límite viene definido por un anillo exterior y dos anillos interiores. El área contenida en los anillos interiores forma parte del exterior del ST_Polygon. (3) es un ST_Polygon permitido, porque los anillos se intersecan en un único punto tangente.

La parte exterior y los anillos interiores definen el límite de un tipo ST_Polygon y el espacio cerrado entre los anillos define el interior de ST_Polygon. Los anillos de un tipo ST_Polygon pueden intersecarse en un punto tangente pero nunca cruzarse. Además de las demás propiedades inherentes de la ST_Geometry de superclase, ST_Polygon tiene área.

Las funciones que operan en un ST_Polygon incluyen lo siguiente:

• ST_Area: devuelve el área de un ST_Polygon como un número de precisión doble
• ST_Centroid: devuelve un ST_Point que representa el centro del contorno del ST_Polygon
• ST_ExteriorRing: devuelve el anillo exterior de un ST_Polygon como ST_LineString
• ST_InteriorRingN: evalúa un ST_Polygon y un índice, y devuelve el anillo interior n como un ST_LineString
• ST_NumInteriorRing: devuelve la cantidad de anillos interiores que contiene un ST_Polygon
• ST_PointOnSurface: devuelve un ST_Point que se garantiza que está en la superficie del ST_Polygon especificado

ST_MultiPolygon

El límite de un ST_MultiPolygon es la longitud acumulativa del anillo exterior e interior de sus elementos. El interior de un tipo ST_MultiPolygon se define como los interiores acumulados de su elemento ST_Polygons. El límite de los elementos de un tipo ST_MultiPolygon solo se puede intersecar en un punto tangente. Además de las demás propiedades inherentes de la ST_Geometry de superclase, ST_MultiPolygons tiene área. ST_MultiPolygons define las entidades, tales como un estrato de un bosque o una parcela no contigua de tierra, como una cadena de islas del Pacífico.

El gráfico siguiente proporciona ejemplos de ST_MultiPolygon: (1) es un ST_MultiPolygon con dos elementos ST_Polygon. El límite viene definido por los dos anillos exteriores y los tres anillos interiores. (2) es un ST_MultiPolygon con dos elementos ST_Polygon. El límite se define mediante los dos anillos exteriores y los dos anillos interiores. Los dos elementos ST_Polygon se intersecan en un punto de tangente.

Las funciones que operan en ST_MultiPolygons incluyen ST_Area, ST_Centroid y ST_PointOnSurface.

La función ST_Area devuelve un número de doble precisión que representa el ST_Area acumulado de los elementos de ST_Polygon de ST_MultiPolygon.

La función ST_Centroid devuelve un ST_Point que es el centro de un contorno de un ST_MultiPolygon.

La función ST_PointOnSurface evalúa un ST_MultiPolygon y devuelve un ST_Point que se garantiza que es normal para la superficie de uno de sus elementos ST_Polygon.

Geometrías simples en una geometría multiparte

Las geometrías multiparte están compuestas de geometrías simples individuales.

Es posible que necesite determinar cuántas geometrías individuales hay en una geometría multiparte, como ST_MultiPoint, ST_MultiLineString y ST_MultiPolygon. Para hacer esto, utilice la función de predicado ST_NumGeometries. Esta función devuelve la cuenta de los elementos individuales en un conjunto de geometrías.

Al usar la función ST_GeometryN, puede determinar qué geometría en la geometría multiparte existe en la posición N, siendo N un número que usted proporciona con la función. Por ejemplo, si desea devolver el tercer punto de una geometría multipunto, debería incluir 3 cuando ejecute la función.

Para devolver las geometrías individuales y su posición desde una geometría multiparte en PostgreSQL, use la función ST_GeomFromCollection.

Interior, límite, exterior

Todas las geometrías ocupan una posición en un espacio definido por sus interiores, límites y exteriores. El exterior de una geometría es todo espacio no ocupado por la geometría. El interior es el espacio ocupado por la geometría. El límite de una geometría es la ubicación entre el interior y el exterior. El subtipo hereda las propiedades interiores y exteriores directamente; sin embargo, la propiedad del límite es diferente para cada uno.

Utilice la función ST_Boundary para determinar la fuente del límite de ST_Geometry. Consulte ST_Boundary para obtener la sintaxis y un ejemplo.

Simple o no simple

Algunos subtipos de ST_Geometry son siempre simples, como ST_Points o ST_Polygons. Sin embargo, los subtipos ST_LineStrings, ST_MultiPoints y ST_MultiLineStrings pueden ser simples y no simples. Son simples si obedecen todas las reglas topológicas que se les impone, y no simples si no lo hacen.

Algunas reglas topológicas incluyen:

• El tipo ST_LineString es simple si no se interseca con el interior, y no simple si lo hace.
• Un ST_MultiPoint es simple si no hay dos de sus elementos ocupando el mismo espacio de coordenada (tiene las mismas coordenadas x,y) y es no-simple si lo hacen.
• Un ST_MultiLineString es simple si ninguno de los interiores de sus elementos se intersecan con su propio interior y es no-simple si alguno de los interiores de los elementos se intersecan.

La función de predicado ST_IsSimple se usa para determinar si un ST_LineString, ST_MultiPoint o ST_MultiLineString es simple o no simple. ST_IsSimple toma un ST_Geometry y devuelve 1 (TRUE) si ST_Geometry es simple, y 0 (FALSE) si no lo es. Consulte ST_IsSimple para obtener la sintaxis y un ejemplo del uso de esta función.

Vacío o no vacío

Una geometría está vacía si no tiene ningún punto. Una geometría vacía tiene sobre, límite, interior y exterior nulos. Una geometría vacía es siempre simple. Las cadenas de líneas y las multicadenas de líneas tienen longitud 0. Los polígonos y los multipolígonos tienen área 0.

La función de predicado ST_IsEmpty puede usarse para determinar si una geometría está vacía. Analiza un ST_Geometry y devuelve 1 (TRUE) si ST_Geometry es simple, y 0 (FALSE) si no lo es. Consulte ST_IsEmpty para obtener la sintaxis y un ejemplo del uso de esta función.

IsClosed e IsRing

Las geometrías de cadena de texto de líneas pueden ser cerradas o anillos. Las cadenas de texto de líneas pueden ser cerradas sin ser anillos. Puede determinar si una cadena de texto de líneas es cerrada mediante la función de predicado ST_IsClosed; devuelve TRUE si el punto de inicio y el extremo de la cadena de texto de línea se intersecan. Los anillos son cadenas de texto de línea que están cerradas y son simples. La función de predicado ST_IsRing puede usarse si una cadena de texto de línea es verdaderamente un anillo; devuelve TRUE si la cadena de texto de línea están cerradas y es simple.

Consulte ST_IsClosed y ST_IsRing para obtener la sintaxis y ejemplos.

Contorno

Cada geometría tiene un sobre. El sobre de una geometría es la geometría de delimitación formada por las coordenadas x,y mínima y máxima. Para geometrías de punto, dado que las coordenadas x,y máximas y mínimas son las mismas, se crea un rectángulo, o sobre, alrededor de estas coordenadas. Para geometrías de línea, los extremos de la línea representan dos lados del sobre y los otros dos lados se crean justo encima y justo debajo de la línea.

La función ST_Envelope toma un ST_Geometry y devuelve un ST_Geometry que representa la fuente del contorno de ST_Geometry. Consulte ST_Envelope para obtener la sintaxis y un ejemplo.

Para encontrar las coordenadas x,y mínimas y máximas individuales de una geometría, utilice las funciones ST_MinX, ST_MinY, ST_MaxX y ST_MaxY.

Sistema de referencia espacial

El sistema de referencia espacial identifica la matriz de transformación de coordenadas para cada geometría. Está compuesto por un sistema de coordenadas, una resolución y una tolerancia.

Todos los sistemas de referencia espacial conocidos para la geodatabase se almacenan en la tabla spatial_references.

Existen dos funciones que se usan para obtener información sobre los sistemas de referencia espacial de las geometrías: ST_SRID y ST_EqualSRS.

La función ST_SRID toma un ST_Geometry y devuelve su identificador de referencia espacial como un número entero.

La función ST_EqualSRS determina si los sistemas de referencias espaciales de dos clases de entidades diferentes son idénticos o no.

Para obtener la sintaxis y los ejemplos de estas funciones, consulte ST_SRID y ST_EqualSRS.

Puede obtener más información sobre las referencias espaciales en el tema Las propiedades de una referencia espacial. Si usa una base de datos de IBM, consulte IBM Db2 Spatial Extender and geodetic Extender User's Guide and Reference o IBM Informix Spatial DataBlade Module User's Guide.

Tamaño de las entidades (solo PostgreSQL)

Las entidades (registros espaciales en una tabla) toman una cierta cantidad de espacio de almacenamiento en bytes. Puede utilizar la función ST_GeoSize para determinar el tamaño de cada entidad en una tabla.