Disponible avec une licence Spatial Analyst.
Il n'est pas obligatoire d'utiliser la même résolution de cellule pour enregistrer différents jeux de données raster. Toutefois, lors du traitement de plusieurs jeux de données, la résolution des cellules, comme leur enregistrement, devraient dans l'idéal être identiques. Lorsque plusieurs jeux de données raster sont entrés dans un outil de l'Extension ArcGIS Spatial Analyst et que leurs résolutions sont différentes, un ou plusieurs d'entre eux sont automatiquement ré-échantillonnés au niveau de résolution le plus grossier des jeux de données raster en entrée.
Dans le cas par défaut, la méthode de rééchantillonnage d'affectation par le voisin le plus proche est utilisée. C'est parce qu'elle peut s'appliquer à la fois aux valeurs discrètes et aux valeurs continues, alors que les autres types de rééchantillonnage - interpolation bilinéaire et convolution cubique - s'appliquent uniquement aux données continues. Il est nécessaire de recourir à une technique de rééchantillonnage car les centres des cellules en entrée sont rarement alignés sur ceux des cellules transformées de la résolution souhaitée. L'interpolation bilinéaire et la convolution cubique peuvent être appliquées avec l'outil Ré-échantillonner comme une étape de prétraitement avant de combiner les rasters de résolutions différentes.
La résolution de rééchantillonnage par défaut peut être contrôlée par le biais du paramètre d'environnement Taille de cellule, où vous pouvez spécifier que l'outil doit utiliser la résolution minimale des rasters en entrée ou une taille de cellule spécifique que vous définissez.
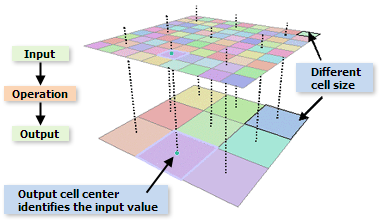
Dans l'image ci-dessous, la taille de cellule définie dans l'environnement d'analyse est plus grossière que celle du raster en entrée de l'outil. Au moment de l'exécution, le raster en entrée est ré-échantillonné à une résolution plus grossière, puis l'outil est appliqué.
Lorsque vous effectuez une analyse, veillez à adapter vos questions à la taille de la cellule. Par exemple, il est peu probable qu'une cellule de 5 kilomètres serve à étudier les déplacements d'une souris. Les cellules de cette taille sont plus indiquées pour examiner les effets du réchauffement de la planète.
Rééchantillonnage
Pour trouver la valeur à attribuer à chaque cellule sur le raster en sortie ré-échantillonné, le centre de chaque cellule dans les données en sortie doit être mappé au système de coordonnées d'origine. Chaque coordonnée du centre de la cellule reprend sa valeur de départ afin d'identifier l'emplacement du point sur le raster en entrée d'origine. Lorsque l'emplacement en entrée est identifié, une valeur peut être attribuée à l'emplacement en sortie en fonction des cellules voisines dans les données en entrée. Il est rare qu'un centre de cellule en sortie s'aligne exactement sur un centre de cellule du raster en entrée. Des techniques ont donc été élaborées pour déterminer la valeur en sortie en fonction de l'emplacement du point par rapport au centre des cellules du raster en entrée et des valeurs associées à ces cellules. Les trois techniques pour déterminer les valeurs en sortie sont les suivantes affectation par le voisin le plus proche, interpolation linéaire et convolution cubique. Chacune attribue des valeurs aux données en sortie de manière différente. Ainsi, les valeurs affectées aux cellules d'un raster en sortie peuvent différer selon la technique employée.
Affectation par le voisin le plus proche
L'affectation par le voisin le plus proche est la technique de rééchantillonnage la plus adaptée aux données discrètes (catégoriques) car elle ne modifie pas la valeur des cellules en entrée. Lorsque l'emplacement du centre de la cellule sur un jeu de données raster en sortie est localisé sur le raster en entrée, l'affectation par le voisin le plus proche détermine l'emplacement du centre de la cellule la plus proche sur le raster en entrée et attribue la valeur de cette cellule à la cellule sur le raster en sortie.
L'affectation par le voisin le plus proche ne modifie aucune des valeurs des cellules du jeu de données raster en entrée. La valeur 2 dans le raster en entrée restera la valeur 2 dans le raster en sortie et ne sera jamais 2,2 ou 2,3. Comme les valeurs des cellules en sortie restent inchangées, l'affectation par le voisin le plus proche doit être utilisée pour les données nominales ou ordinales où chaque valeur représente une classe, un membre ou une classification (données catégoriques, telles que l'occupation des sols ou un type de sol ou de forêt).
Prenons l'exemple d'un raster en sortie créé à partir d'un raster en entrée pivoté de 45° lors d'une opération, qui sera par conséquent ré-échantillonné. Pour chaque cellule en sortie, il est nécessaire de dériver une valeur du raster en entrée. Dans l'illustration ci-dessous, les centres des cellules du raster en entrée sont les points gris. Les cellules en sortie sont ombrées en vert. La cellule qui est traitée est ombrée en jaune. Dans l'affectation par le voisin le plus proche, le centre de cellule du raster en entrée qui est plus proche (point orange) du centre de cellule traitée (point rouge) est identifié et est affecté en tant que valeur en sortie pour la cellule traitée (jaune ombré). Ce processus est répété pour chaque cellule dans le raster en sortie.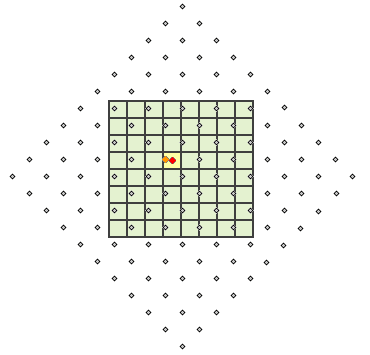
Interpolation bilinéaire
L'interpolation bilinéaire utilise la valeur du centre des quatre cellules en entrée les plus proches pour déterminer la valeur sur le raster en sortie. La nouvelle valeur pour la cellule en sortie correspond à la moyenne pondérée de ces quatre valeurs, ajustée pour tenir compte de la distance les séparant du centre de la cellule en sortie. Cette méthode d'interpolation crée une surface à l'aspect plus lisse qu'avec l'affectation par le voisin le plus proche.
Dans l'illustration suivante, comme dans la précédente pour le principe d'interpolation du voisin le plus proche, les centres des cellules du raster en entrée sont des points gris, les cellules en sortie sont ombrées en vert, et la cellule qui est traitée est ombrée en jaune. Pour l'interpolation bilinéaire, les quatre centres de cellule en entrée (points orange) les plus proches du centre de la cellule traitée (point rouge) sont identifiés, la moyenne pondérée est calculée, et la valeur résultante est affectée en tant que valeur en sortie pour la cellule traitée (jaune ombré).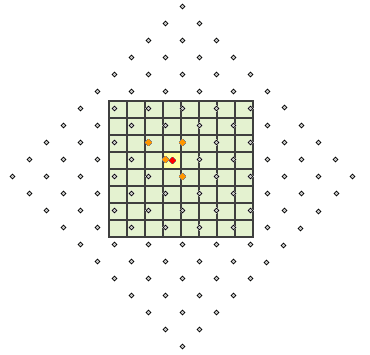
Puisque les valeurs des cellules en sortie sont calculées en fonction de la position relative et de la valeur des cellules en entrée, l'interpolation bilinéaire est préférable pour les données où l'emplacement à partir d'un point ou phénomène connu définit la valeur attribuée à la cellule (c'est-à-dire surfaces continues). L'altitude, la pente, l'intensité du bruit d'un aéroport et la salinité de l'eau près d'un estuaire sont tous des phénomènes représentés sous la forme de surfaces continues et qui sont ré-échantillonnés à l'aide de l'interpolation bilinéaire.
Convolution cubique
La convolution cubique est similaire à l'interpolation bilinéaire mais la moyenne pondérée est calculée à partir des centres des 16 cellules en entrée les plus proches et de leurs valeurs.
L'illustration suivante montre comment la valeur en sortie est calculée pour la convolution cubique. Les 16 centres de cellules en entrée (points orange) les plus proches du centre de la cellule traitée (point rouge) sont identifiés, la moyenne pondérée est calculée, et la valeur résultante est affectée en tant que valeur en sortie pour la cellule traitée (jaune ombré).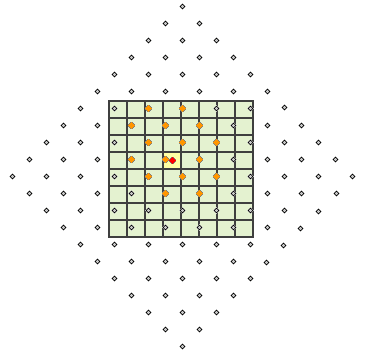
La convolution cubique a tendance à davantage affiner les limites des données que l'interpolation bilinéaire car le calcul de la valeur en sortie nécessite plus de cellules.
Rééchantillonnage et types de données
L'interpolation bilinéaire ou la convolution cubique ne doivent pas être utilisées sur des données catégorielles, puisque les catégories ne sont pas conservées dans le jeu de données raster en sortie. Cependant, les trois techniques peuvent s'appliquer aux données continues, le voisin le plus proche produisant la sortie la plus rugueuse, l'interpolation bilinéaire la sortie la plus lisse et la convolution cubique les résultats les plus fins.