Disponible avec une licence Spatial Analyst.
Le transport d'un soluté dans un milieu poreux implique deux mécanismes principaux : l'advection et la dispersion hydrodynamique. L'advection décrit le transport passif d'un soluté avec le liquide transportant. La dispersion est le mélange du soluté avec le liquide par mouvement différentiel des liquides à travers les espaces poreux. L'outil Concentration part du principe que l'aquifère est mélangé verticalement, c'est-à-dire que la concentration est la même sur une section verticale. Cela permet d'employer un modèle mathématique en deux dimensions, conformément au modèle de données du raster.
Dispersion bidimensionnelle
La dispersion bidimensionnelle dans un milieu poreux est régie par l'équation d'advection-dispersion (Bear, 1979, Freeze et Cherry, 1979 et Marsily, 1986) élaborée en termes de directions longitudinale (dans la direction du flux) et transversale (perpendiculaire à la direction du flux) XL et XT, comme suit :
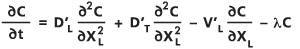
- où :
C : concentration du soluté sous la forme d'une fonction de deux dimensions spatiales et d'une durée t.
∂C/∂t : représente la durée temporelle.
D'L : coefficients de dispersion (retenue) effectifs dans la direction longitudinale.
D'T : coefficients de dispersion (retenue) effectifs dans la direction transversale.
λ : coefficient de désintégration, censé être une constante pour la désintégration exponentielle de premier degré.
Coefficients de dispersion
Le coefficient de dispersion est une mesure de l'étendue selon laquelle le soluté se disperse dans la direction définie:
D'i = Di/R
- où :
R : facteur de rétention.
i : direction (longitudinale ou transversale).
Le coefficient de dispersion est associé au comportement du soluté dans un milieu particulier.
Relation entre la dispersivité et le coefficient de dispersion
Les dispersivités αL (dispersivité longitudinale) et αT (issue du ratio de dispersivité) relèvent de coefficients de dispersion :
D'L = αL V' et
D'T = αT V'
où :
V' : la vitesse retenue moyenne de la concentration.
XL : déplacement dans la direction longitudinale, parallèle à la direction du flux au niveau du centroïde de la masse.
XT : déplacement dans la direction transversale, perpendiculaire à la direction du flux au niveau du centroïde de la masse.
V'L : vitesse du soluté retenu dans la direction longitudinale.
Flux entrant dans la nappe phréatique :
V = q / n
- où :
q : flux de Darcy (débit par aire de section mouillée).
n : porosité réelle de la formation géologique.
V' = V / R
Reportez-vous à la documentation relative à la vitesse de Darcy pour une discussion plus détaillée sur les rapidités de transport.
dispersion gaussienne
La solution approximative de cette équation utilisée avec l'outil Concentration repose sur l'hypothèse de la dispersion gaussienne d'une source de points instantanés dans un domaine bidimensionnel avec une concentration initiale nulle (par exemple, un aquifère propre mélangé verticalement). Le calcul fait intervenir l'équation suivante :
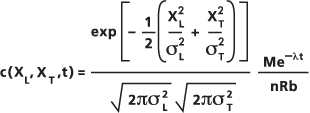
- où :
M : masse du soluté libéré instantanément à la source, en unités de masse.
n : porosité de l'aquifère.
R : facteur de rétention.
b : épaisseur de l'aquifère en unités de longueur.
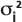: variance de la répartition gaussienne dans les directions longitudinale et transversale, déterminée en tant que fonction de la dispersivité longitudinale et du rapport de dispersivité que vous indiquez, ainsi que la longueur de la trajectoire depuis le centre de la masse du soluté obtenu dans le fichier de suivi.
La forme elliptique générale de cette fonction de répartition gaussienne bivariée est illustrée ci-dessous :
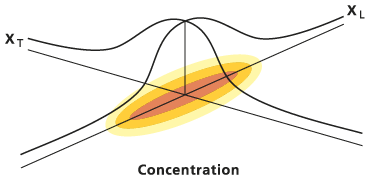
Il existe plusieurs restrictions significatives et des hypothèses liées à l'emploi de l'outil Concentration. L'ellipse de répartition est centrée dans la masse du soluté, qui est censée s'être déplacé en suivant la trajectoire du flux, décrite dans le fichier en entrée. L'orientation de l'ellipse est également déterminée par la trajectoire du flux, l'axe principal étant tangent à la trajectoire au niveau du centroïde. La porosité et l'épaisseur, qui contribuent également à la répartition, sont interpolées de leurs rasters respectifs au niveau du centroïde, en n'incorporant aucune information sur les cellules voisines. Vous entrez la rétention, le temps, le coefficient de désintégration, la dispersivité longitudinale et le rapport de dispersivité sous forme de constantes.
Dispersivité
La dispersivité est un paramètre qui détermine la dispersion d'un soluté à travers un milieu poreux et qui est défini en unités de longueur. Dans un modèle de concentration, la dispersivité est utilisée pour calculer la variance.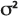 
de l'équation de dispersion gaussienne ci-dessus, selon :
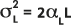et 
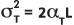
La nature de la dispersivité et les méthodes permettant de la déterminer sont des sujets qui offrent matière à débattre et auxquels la communauté de modélisation des nappes phréatiques porte un vif intérêt. Il n'existe à ce jour aucun moyen universellement accepté qui permette d'estimer ses valeurs. Vous trouverez des informations relatives aux dispersivités de diverses formations géologiques dans les travaux de Gelhar et al. (1992).
Le diagramme suivant récapitule une variété de données issues d'ouvrages publiés et met en rapport la dispersivité longitudinale avec l'échelle du problème concerné, c'est-à-dire la distance séparant l'emplacement source du point d'observation.
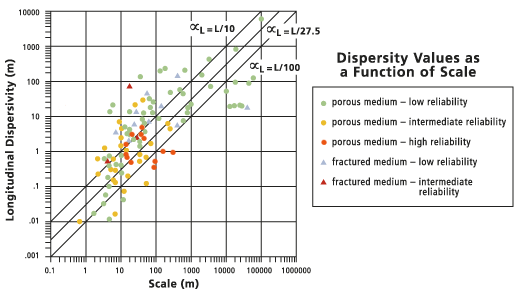
La ligne continue (ou la ligne centrale) du graphique représente la valeur par défaut de la dispersivité longitudinale calculée avec la fonction Concentration.
La ligne est créée à partir d'un ajustement de régression linéaire de
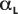vers L, ce qui se traduit par 
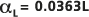ou une classe de 
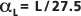, dans laquelle la longueur de la trajectoire L est l'échelle d'observation.Les statistiques de cette régression sont également présentées ci-dessous. Les lignes interrompues externes sont placées à
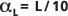et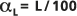 
pour comparaison.
Ce calcul par défaut doit être utilisé à titre informatif uniquement, étant donné que certains chercheurs dénoncent l'utilisation d'un tel ajustement universel. Pour des échelles ou des sites particuliers, les dispersivités valides sont comprises entre deux ordres de grandeur, l'estimation la plus fiable tendant vers les valeurs les moins élevées. Plutôt que d'utiliser la valeur par défaut, qui n'a aucune base théorique, envisagez d'effectuer plusieurs simulations en utilisant une plage de dispersivités. L'étude d'une série de résultats est plus fiable que l'utilisation des résultats d'une simulation.
Des mises en garde similaires s'appliquent à l'évaluation du rapport de dispersivité longitudinale sur la dispersivité transversale, présenté dans la figure suivante. Ces valeurs sont généralement associées par un rapport simple, bien qu'il soit préférable de tester une plage de valeurs.
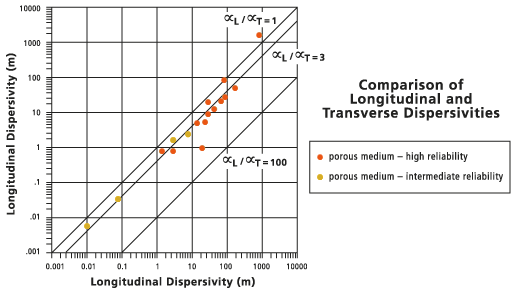
Le rapport de dispersivité par défaut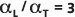 
est représenté par la ligne continue (ligne centrale) dans la figure ci-dessous. Les lignes interrompues (externes) sont placées à 
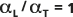et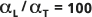 
pour comparaison.
Gelhar et al inclut des valeurs pour la porosité réelle et la transmissivité dans la tabulation. Les tables de ces valeurs sont présentées dans les travaux de Freeze et Cherry (1979) et de Marsily (1986).
Rétention
La rétention, c'est-à-dire le rapport entre la vitesse du liquide transportant et celle du soluté, est exprimée sous la forme d'un nombre compris entre 1 et l'infini, sans unités. Une rétention de 2 signifie que le soluté se déplace dans le milieu poreux à la moitié de la vitesse d'infiltration. Le traceur idéal ne subit aucune adsorption et circule dans la solution avec le liquide. Un tel soluté a une rétention égale à 1, c'est-à-dire qu'il se déplace à la même vitesse que le liquide transportant.
Ce phénomène est le résultat de l'adsorption et de la désorption du constituant dans la matrice poreuse, notamment dans les films organiques de parois poreuses. L'équation de rétention est présentée dans un essai de Freeze et Cherry (1979) comme suit :
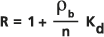
où :
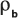: densité brute de la matrice.n : porosité de la formation.
Kd : coefficient de répartition qui représente le partitionnement suite à l'adsorption réversible rapide d'un soluté entre les phases liquide et solide en émettant l'hypothèse d'un isotherme linéaire.
Marsily (1986) aborde également en détail le facteur de rétention et l'adsorption.
Modélisation d'une advection-dispersion
Les outils Flux de Darcy, Suivi de particules et Concentration permettent d'effectuer une modélisation d'advection-dispersion rudimentaire des composants d'une nappe phréatique. L'outil Flux de Darcy crée un flux dans une nappe phréatique dont la vitesse est fonction des données géologiques. L'outil Suivi de particules suit le trajet de l'advection depuis la source et l'outil Concentration permet de calculer la dispersion hydrodynamique d'un point instantané qui se trouve dans le flux.
Une discussion complète sur la modélisation de l'advection-dispersion avec ces outils est présentée par Tauxe (1994).
La séquence typique pour la modélisation de la dispersion de la nappe phréatique consiste à utiliser les outils Flux de Darcy, puis Suivi de particules, puis Concentration.
Exemple
- Vous trouverez ci-après un exemple de la boîte de dialogue de l'outil Concentration :
Fichier de suivi de particules en entrée : ttrack.txt
Raster de porosité effective de la formation en entrée : poros
Raster d'épaisseur saturée en entrée : thickn
Raster en sortie : ppuff1
Masse : 3.2e7
Temps de dispersion : 50000
Dispersivité longitudinale : 6
Rapport de dispersivité : 3
Facteur de rétention : 1
Coefficient de désintégration : 250
- Exemple d'utilisation de l'outil Concentration dans Algèbre spatial :
outPPuff1 = PorousPuff(ttrack.txt, poros, thickn, 1000000, 0.01, 10, 1.5, 1.0, 500)
- Vous trouverez ci-après un exemple d'expression d'algèbre spatial faisant intervenir des outils de modélisation d'une nappe phréatique :
out_vol = DarcyFlow(head, poros, thickn, transm, dir1, mag1) ParticleTrack(dir1, mag1, ttrack.txt, 500, 650, "#", "#", track_feat.shp) out_puff = PorousPuff(ttrack.txt, poros, thickn, 3.2e7, 50000, 6, 3, 1, 250)
Bibliographie
Bear, J. 1979, Hydraulics of Groundwater. McGraw–Hill.
Freeze, R. A. et J. A. Cherry. 1979. Groundwater. Prentice–Hall.
Gelhar, L. W., C. Welty et K. R. Rehfeldt. 1992. "A Critical Review of Data on Field-Scale Dispersion in Aquifers". Water Resources Research 28 (7) : 1955–1974.
Marsily, G. de. 1986. Quantitative Hydrogeology. Academic Press.
Tauxe, J. D. 1994. "Porous Medium Advection–Dispersion Modeling in a Geographic Information System". Essai thèse doct, University of Texas, Austin.