Disponible avec une licence Spatial Analyst.
Pour chaque cellule, l'outil Pente calcule le taux de variation maximal des valeurs de cette cellule par rapport à ses voisines. D'une façon générale, la variation maximale de l'altitude sur la distance entre la cellule et ses huit voisines identifie la descente la plus raide depuis la cellule.
En théorie, l'outil ajuste un plan aux valeurs z d'un voisinage de 3 x 3 cellules autour de la cellule de traitement ou centrale. La valeur de pente de ce plan est calculée à l'aide de la technique maximale moyenne (voir Références). La direction dans laquelle le plan est orienté est l'exposition de la cellule de traitement. Plus la valeur de la pente est faible, plus le terrain est plat ; plus la valeur de la pente est élevée, plus le terrain est pentu.
Si un emplacement de cellule avec la valeur NoData z est présent dans le voisinage, la valeur z de la cellule centrale sera attribuée à l'emplacement. Sur le tronçon du raster, au moins trois cellules (à l'extérieur de l'étendue du raster) contiendront NoData en tant que valeurs z. La valeur z de la cellule centrale sera affectée à ces cellules. Le résultat est un aplatissement du plan 3 x 3 ajusté à ces tronçons, qui génère habituellement une diminution de la pente.
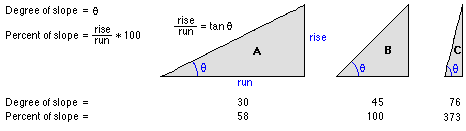
Le raster de pente en sortie peut être calculé dans deux types d'unités : degrés ou pourcentage (pourcentage d'élévation). Le pourcentage d'élévation peut être mieux compris si vous le considérez comme la hauteur calculée divisée par le parcours, multipliée par 100. Consultez le triangle B ci-dessous. Lorsque l'angle est de 45 degrés, la hauteur calculée est égale au parcours et le pourcentage d'élévation est de 100 pour cent. Lorsque l'angle de pente se rapproche de la verticale (90 degrés), comme dans le triangle C, le pourcentage d'élévation se rapproche de l'infini.
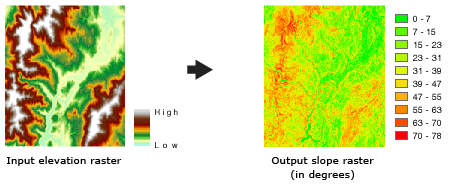
L'outil Pente est généralement appliqué à un jeu de données d'altitude, comme le montrent les diagrammes ci-dessous. Les pentes les plus raides apparaissent sur le raster de pente en sortie sous forme de couleur ombrée rouge.
L'outil peut également être utilisé avec d'autres types de données continues, telles que des données de population, afin d'identifier d'importantes variations de valeur.
Algorithme de pente
Les taux de variation (delta) de la surface dans les directions horizontale (dz/dx) et verticale (dz/dy) à partir de la cellule centrale déterminent la pente. L'algorithme de base utilisé pour calculer la pente est :
slope_radians = ATAN ( √ ([dz/dx]2 + [dz/dy]2) )La pente est généralement mesurée en degrés, comme dans l'algorithme suivant :
slope_degrees = ATAN ( √ ([dz/dx]2 + [dz/dy]2) ) * 57.29578L'algorithme de pente peut aussi être interprété comme :
slope_degrees = ATAN (rise_run) * 57.29578- où :
rise_run = √ ([dz/dx]2 + [dz/dy]2]
Les valeurs de la cellule centrale et de ses huit voisines déterminent les deltas horizontaux et verticaux. Les voisines sont identifiées par les lettres a à i ; e représentant la cellule pour laquelle l'exposition est calculée.
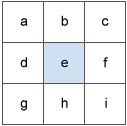
Le taux de variation dans la direction x pour la cellule e est calculé avec l'algorithme suivant :
[dz/dx] = ((c + 2f + i) - (a + 2d + g) / (8 * x_cellsize)Le taux de variation dans la direction y pour la cellule e est calculé avec l'algorithme suivant :
[dz/dy] = ((g + 2h + i) - (a + 2b + c)) / (8 * y_cellsize)Exemple de calcul de la pente
Dans cet exemple, la valeur de pente de la cellule centrale de la fenêtre mobile présentée ci-dessous sera calculée.
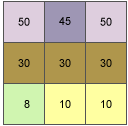
La taille de cellule est 5 unités. La mesure de pente par défaut en degrés sera utilisée.
Le taux de variation dans la direction x pour la cellule centrale e est :
[dz/dx] = ((c + 2f + i) - (a + 2d + g) / (8 * x_cellsize)
= ((50 + 60 + 10) - (50 + 60 + 8)) / (8 * 5)
= (120 - 118) / 40
= 0.05Le taux de variation dans la direction y pour la cellule e est :
[dz/dy] = ((g + 2h + i) - (a + 2b + c)) / (8 * y_cellsize)
= ((8 + 20 + 10) - (50 + 90 + 50)) / (8 * 5)
= (38 - 190 ) / 40
= -3.8En se basant sur le taux de variation dans les directions x et y, la pente de la cellule centrale e est calculée comme suit :
rise_run = √ ([dz/dx]2 + [dz/dy]2)
= √ ((0.05)2 + (-3.8)2)
= √ (0.0025 + 14.44)
= 3.80032 slope_degrees = ATAN (rise_run) * 57.29578
= ATAN (3.80032) * 57.29578
= 1.31349 * 57.29578
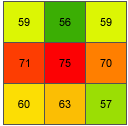
= 75.25762La valeur entière de la pente de la cellule e est 75 degrés.
Référence
Burrough, P. A. et McDonell, R. A., 1998. Principles of Geographical Information Systems (Oxford University Press, New York), 190 pp.