Ce document fournit des informations supplémentaires sur les paramètres des outils et présente également le vocabulaire et les concepts essentiels pour l'analyse de données à l'aide des Outils de statistiques spatiales. Consultez-le lorsque vous avez besoin d'informations supplémentaires sur les paramètres des outils.
Conceptualisation des relations spatiales
Une différence importante entre statistiques spatiales et classiques (aspatiales ou non spatiales) est que les premières intègrent l'espace et les relations spatiales directement dans leurs formules mathématiques. En conséquence, un grand nombre des outils de la boîte à outils Spatial Statistics nécessitent que l'utilisateur sélectionne une valeur pour le paramètre Conceptualisation des relations spatiales avant l'analyse. Parmi les conceptualisations courantes, citons inverse de la distance, temps de trajet, distance constante, K voisins les plus proches et contiguïté. La conceptualisation des relations spatiales que vous utilisez dépend de ce que vous mesurez. Si vous mesurez l'agrégation d'une espèce particulière de plante propagée par les semences, par exemple, l'inverse de la distance est probablement mieux adapté. Cependant, si vous évaluez la distribution géographique des banlieusards d'une région, le temps ou le coût de trajet peuvent être de meilleurs choix pour la description de ces relations spatiales. Pour certaines analyses, l'espace et le temps peuvent être moins importants que d'autres concepts plus abstraits tels que la familiarité (plus une chose est familière, plus elle est fonctionnellement proche) ou l'interaction spatiale (liaisons téléphoniques plus fréquentes entre Los Angeles et New York, par exemple, qu'entre New York et une plus petite ville plus proche de New York, comme Poughkeepsie ; certains diront peut-être que Los Angeles et New York sont fonctionnellement plus proches).
L'outil Analyse des regroupements contient le paramètre Contraintes spatiales, et si les options de ce paramètre sont similaires à celles du paramètre Conceptualisation de relations spatiales, elles s'utilisent différemment. Lorsqu'une contrainte spatiale est imposée, seules les entités qui partagent au moins un voisin (comme cela est défini par les méthodes de contiguïté, de relations de voisin le plus proche ou de triangulation) peuvent appartenir au même groupe. Pour des obtenir des informations et des exemples supplémentaires, consultez la rubrique Fonctionnement de l'outil Analyse des regroupements.
Options du paramètre de Conceptualisation des relations spatiales comme présentées ci-après. L'option que vous sélectionnez détermine les relations voisines pour les outils qui évaluent chaque entité dans le contexte des entités voisines. Ces outils sont notamment Auto-corrélation spatiale (Global Moran's I), Analyse de points chauds (Getis-Ord Gi*) et Analyse de grappes et de valeurs aberrantes (Anselin Local Moran's I). Notez que certaines de ces options sont disponibles uniquement si vous utilisez les outils Générer la matrice de pondérations spatiales ou Générer les pondérations spatiales de réseau.
Inverse de la distance, inverse de la distance au carré (impédance)

Grâce aux options inverse de la distance, le modèle conceptuel des relations spatiales est l'impédance ou la fréquentation en fonction de la distance. Toutes les entités ont un impact/une influence sur les autres entités, mais plus elles sont éloignées, plus cet impact est réduit. Vous devez généralement spécifier une valeur de Canal distance ou distance seuil lorsque vous utilisez une conceptualisation d'inverse de la distance pour réduire le nombre de calculs requis, particulièrement sur des jeux de données volumineux. Si aucun canal distance ou aucune distance seuil n'est spécifié, une valeur seuil par défaut est calculée. Vous pouvez forcer toutes les entités à être voisines de toutes les autres entités en définissant l'option à zéro.
La distance euclidienne inverse est adaptée à la modélisation de données continues, telles que les variations de température, par exemple. L'inverse de la distance de Manhattan peut mieux fonctionner si les analyses impliquent les emplacements de quincailleries ou autres équipements urbains fixes, dans le cas où un réseau routier n'est pas disponible. Lorsque vous utilisez l'option Inverse de la distance au carré , le modèle conceptuel est le même qu'avec Distance inverse hormis que la pente est plus prononcée. Les influences des voisins s'affaiblissent donc plus rapidement et seuls les voisins les plus proches d'une entité cible exercent une influence substantielle dans les calculs de cette entité.
Canal distance (sphère d'influence)

Pour certains outils comme Analyse de points chauds, un canal distance constante est la conceptualisation par défaut des relations spatiales. Avec l'option Canal de distance constante, vous imposez aux données un modèle conceptuel d'interactions spatiales de sphère d'influence ou de fenêtre mobile. Chaque entité est analysée dans le contexte des entités voisines se trouvant à la distance critique que vous spécifiez pour Canal distance ou distance seuil. Les voisins contenus dans la distance spécifiée sont pondérés de manière égale. Les entités se trouvant hors de la distance spécifié n'ont aucune incidence sur les calculs (leur poids est zéro). Adoptez la méthode Canal de distance constante lorsque vous souhaitez évaluer les propriétés statistiques de vos données à une échelle spatiale (fixe) donnée. Si vous étudiez la migration quotidienne de travailleurs et que vous savez que le trajet moyen jusqu'au lieu de travail est de 15 km, par exemple, une distance de 15 km convient pour votre analyse. Vous trouverez ci-après, dans la rubrique Sélection d'une distance constante, les stratégies permettant d'identifier une échelle d'analyse appropriée.
Zone d'indifférence

L'option Zone d'indifférence du paramètre Conceptualisation de relations spatiales combine les modèles Inverse de la distance et Canal de distance constante. Les entités situées dans le canal distance ou la distance seuil sont comprises dans les analyses de l'entité cible. Une fois la distance critique dépassée, le niveau d'influence (la pondération) chute rapidement. Supposons que vous cherchiez un travail et ayez le choix entre un travail situé à cinq kilomètres et un autre situé à six kilomètres. Vous ne tiendrez probablement pas beaucoup compte de la distance lorsque vous déciderez quel travail accepter. Maintenant, supposons que vous ayez le choix entre un travail situé à cinq kilomètres et un autre situé à vingt kilomètres. Dans ce cas, la distance est plus une impédance et elle peut être prise en compte dans la décision. Utilisez cette méthode si vous voulez conserver l'échelle d'analyse fixe, mais que vous ne souhaitez pas imposer des limites strictes sur les entités voisines incluses dans les calculs d'entités cible.
Contiguïté de polygones (premier ordre).
Pour les classes d'entités surfaciques, vous pouvez sélectionner CONTIGUITY_EDGES_ONLY (parfois appelé "Rook's Case") ou CONTIGUITY_EDGES_CORNERS (parfois appelé "Queen's Case"). Dans le cas de CONTIGUITY_EDGES_ONLY, les polygones qui partagent une limite (dont des limites coïncident) sont inclus dans les calculs du polygone cible. Les polygones qui ne partagent pas de limite sont exclus des calculs d'entités cible. Pour CONTIGUITY_EDGES_CORNERS, les polygones qui partagent un bord et/ou un angle sont inclus dans les calculs pour le polygone cible. Si deux polygones se chevauchent en partie, ils sont considérés comme étant voisins et sont inclus dans leurs calculs réciproques. Utilisez l'une de ces conceptualisations de contiguïté avec des entités surfaciques si vous modélisez un type de processus contagieux ou si vous utilisez des données continues représentées sous la forme de polygones.
K voisins les plus proches
Les relations de voisinage peuvent également être conçues de sorte que chaque entité soit évaluée dans le contexte spatial du nombre spécifié de ses voisins les plus proches. Si K (le nombre de voisins) est 8, les huit voisins les plus proches de l'entité cible seront inclus dans les calculs pour cette entité. Sur les sites à densité d'entités élevée, le contexte spatial de l'analyse sera réduit. De la même façon, sur les sites à densité d'entités faible, le contexte spatial de l'analyse sera plus important. Un avantage de ce modèle de relations spatiales est qu'il garantit l'existence de voisins pour chaque entité cible, même si les densités cible présentent de fortes variations dans la zone d'étude. Cette méthode est disponible dans l'outil Générer la matrice de pondérations spatiales. L'option K_NEAREST_NEIGHBORS avec 8 comme valeur du paramètre Nombre de voisins est la conceptualisation par défaut utilisée avec la régression exploratoire pour évaluer les valeurs résiduelles de régression.
Triangulation de Delaunay (voisins naturels)
L'option Triangulation de Delaunay construit des voisins en créant des triangles de Voronoi à partir d'entités ponctuelles ou de centroïdes d'entités de sorte que chaque point/centroïde soit un nœud de triangle. Les nœuds connectés par le bord d'un triangle sont considérés comme voisins. L'utilisation de la triangulation de Delaunay garantit que chaque entité possède au moins un voisin, même si les données incluent des îles et/ou des densités d'entités très variables. N'utilisez pas la triangulation de Delaunay si certaines entités coïncident. Cette méthode est disponible dans l'outil Générer la matrice de pondérations spatiales.

Fenêtre spatio-temporelle
Cette option permet de définir des relations entre entités en termes de fenêtres d'espace (distance constante) et de temps (intervalle temporel constant). Cette option est disponible quand vous créez un fichier de matrice de pondérations spatiales à l'aide de l'outil Générer la matrice de pondérations spatiales. Lorsque vous sélectionnez SPACE_TIME_WINDOW, vous devez spécifier une valeur pour les paramètres suivants : Champ de date/heure, Type d'intervalle de date/heure (HOURS, DAYS ou MONTHS, par exemple) et Valeur d'intervalle de date/heure. La valeur d'intervalle est un entier. Si, par exemple, vous avez sélectionné HOURS comme type d'intervalle et 3 comme valeur d'intervalle, deux entités seront considérées comme voisines si les valeurs de leur champ de date/heure ont moins de trois heures d'écart. Avec cette conceptualisation, les entités sont voisines si elles se trouvent dans la limite de distance spécifiée et si elles sont comprises dans l'intervalle de temps spécifié de l'entité cible. Par exemple, vous sélectionnerez le paramètre SPACE_TIME_WINDOW Conceptualisation de relations spatiales si vous voulez créer un fichier de matrice de pondérations spatiales à utiliser avec l'outil Analyse de points chauds afin d'identifier les points chauds spatio-temporels. Pour obtenir des informations supplémentaires, dont la procédure à suivre pour visualiser les résultats, consultez la rubrique Analyse spatio-temporelle. D'autres méthodes sont disponibles pour vous aider à visualiser en 3D un cube spatio-temporel netCDF.
Obtenir des relations spatiales à partir d'un fichier (relations spatiales définies par l'utilisateur).
Vous pouvez créer un fichier où stocker les relations de voisinage d'une entité à l'aide de l'outil Générer la matrice de pondérations spatiales ou de l'outil Générer les pondérations spatiales de réseau. Si vous souhaitez définir des relations spatiales à l'aide de la durée ou du coût des trajets dérivés à partir d'un jeu de données réseau, créez un fichier de matrice de pondérations spatiales à l'aide de l'outil Générer les pondérations spatiales de réseau, puis utilisez le fichier SWM résultant pour vos analyses. Si les relations spatiales pour vos entités sont définies dans une table, vous pouvez utiliser l'outil Générer la matrice de pondérations spatiales pour convertir cette table en fichier de matrice de pondérations spatiales (.swm). Vous devez inclure des champs particuliers dans votre table afin d'utiliser l'option CONVERT_TABLE pour obtenir un fichier SWM. Vous pouvez également fournir un chemin d'accès au fichier texte ASCII formaté qui définit votre propre conceptualisation personnalisée des relations spatiales (d'après l'interaction spatiale, par exemple).
Sélection d'une conceptualisation des relations spatiales : pratiques conseillées.
Plus la modélisation de l'interaction des entités dans l'espace est réaliste, plus les résultats sont précis. Le choix du paramètre Conceptualisation de relations spatiales doit refléter les relations inhérentes entre les entités que vous analysez. Votre choix peut également être motivé par les caractéristiques de vos données.
Les méthodes d'inverse de la distance (INVERSE_DISTANCE et INVERSE_DISTANCE_SQUARED), par exemple, sont mieux adaptées aux données continues ou à des processus de modèle dans lesquels, plus deux entités sont proches dans l'espace, plus elles sont susceptibles d'interagir/de s'influencer mutuellement. Grâce à cette conceptualisation spatiale, chaque entité est potentiellement voisine de toutes les autres, et, dans le cas de jeux de données importants, le nombre de calculs impliqués est énorme. Essayez toujours d'inclure une valeur Canal distance ou distance seuil lorsque vous utilisez les conceptualisations d'inverse de la distance. Ce point est particulièrement important pour les jeux de données volumineux. Si vous laissez le paramètre Canal distance ou distance seuil vide, une distance seuil est calculée, mais ce ne sera peut-être pas la distance appropriée pour votre analyse. La distance seuil par défaut est la distance minimale qui garantit que chaque entité possède au moins un voisin.
La méthode FIXED_DISTANCE_BAND est recommandée pour les données ponctuelles. C'est l'option par défaut utilisée par l'outil Hot Spot Analysis (Getis-Ord Gi*). Cette méthode fonctionne bien pour des données surfaciques lorsque la taille des polygones est très variable (polygones très grands à la limite de la zone d'étude et polygones très petits en son centre, par exemple) et que vous voulez garantir une échelle d'analyse constante. Vous trouverez ci-dessous, dans la rubrique Sélection d'une distance constante, les stratégies permettant de déterminer une valeur de canal de distance appropriée pour votre analyse.
La conceptualisation ZONE_OF_INDIFFERENCE fonctionne bien lorsque la distance constante est appropriée, mais l'imposition de limites nettes sur les relations de voisinage ne correspond pas à une représentation précise de vos données. N'oubliez pas que le modèle conceptuel de la zone d'indifférence considère toute entité comme un voisin de toutes les autres entités. Cette option n'est donc pas adaptée aux jeux de données volumineux puisque la valeur Canal distance ou distance seuil fournie ne limite pas le nombre de voisins, mais spécifie uniquement où l'intensité des relations spatiales commence à décroître.
Les conceptualisations de contiguïté des polygones (CONTIGUITY_EDGES_ONLY et CONTIGUITY_EDGES_CORNERS) sont efficaces si les polygones sont de taille et de distribution similaires et que les relations spatiales sont une fonction de la proximité des polygones (si deux polygones partagent une limite, leur interaction spatiale augmente) Lorsque vous sélectionnerez une conceptualisation de contiguïté de polygone, vous souhaiterez presque toujours sélectionner la standardisation par lignes pour les outils possédant le paramètre Standardisation par lignes.
L'option K_NEAREST_NEIGHBORS est efficace lorsque vous souhaitez garantir un nombre minimal de voisins dans l'analyse. Surtout si les valeurs associées aux entités sont faussées (qu'elles ne sont pas distribuées normalement), il est important que chaque entité soit évaluée dans le contexte d'au moins huit voisins (il s'agit là uniquement d'une règle générale). Si la distribution de vos données varie dans votre zone d'étude et que certaines entités sont éloignées de toutes les autres entités, cette méthode fonctionne bien. Notez toutefois que le contexte spatial de votre analyse change selon les variations rencontrées dans la rareté/densité de vos entités. Lorsque la détermination de l'échelle d'analyse est moins importante que la détermination du nombre de voisins, la méthode des K voisins les plus proches est adaptée.
Certains analystes considèrent DELAUNAY_TRIANGULATION comme une méthode permettant de construire des voisins naturels pour un ensemble d'entités. Cette méthode est une bonne option lorsque vos données comprennent des polygones d'îles (des polygones isolés ne partageant aucun bord avec d'autres polygones) ou si la distribution spatiale d'entités est très inégale. Elle n'est cependant pas appropriée si certaines de vos entités coïncident. Similaire à la méthode des K voisins les plus proches, la triangulation de Delaunay garantit que chaque entité possède au moins un voisin, mais qu'elle utilise la distribution des données pour déterminer le nombre de voisins que chaque entité obtient.
Les paramètres de l'option SPACE_TIME_WINDOW permettent de définir des relations entre entités en termes de proximité spatiale et de proximité temporelle. Vous utiliserez cette option pour identifier les hots spots spatiaux-temporels ou créer des groupes pour lesquels l'appartenance a été contrainte par la proximité spatiale et temporelle. Vous trouverez des exemples d'analyse spatio-temporelle, ainsi que des stratégies de représentation efficace des résultats de ce type d'analyse, dans la rubrique Analyse spatio-temporelle.
Pour certaines applications, l'interaction spatiale est mieux modélisée en termes de temps de trajet ou distance à parcourir. Si vous modélisez l'accessibilité de services urbains, par exemple, ou si vous cherchez des points chauds de criminalité urbaine, la modélisation de relations spatiales en termes de réseau est une bonne option. Utilisez l'outil Générer les pondérations spatiales de réseau pour créer un fichier de matrice de pondérations spatiale (.swm) avant l'analyse. Sélectionnez GET_SPATIAL_WEIGHTS_FROM_FILE comme valeur Conceptualisation de relations spatiales, puis pour le paramètre Fichier de matrice de pondérations, indiquez le chemin d'accès complet au fichier SWM que vous avez créé.
Si aucune option du paramètre Conceptualisation de relations spatiales n'est adaptée à votre analyse, vous pouvez créer un fichier texte ASCII ou une table incluant les relations d'entité à entité de votre choix puis les utiliser pour créer un fichier de matrice de pondérations spatiales. Si l'une des options ci-dessus répond presque parfaitement à vos besoins, utilisez l'outil Générer la matrice de pondérations spatiales pour créer un fichier SWM de base, puis modifiez votre fichier de matrice de pondérations spatiales.
Sélection d'une valeur de canal de distance constante
Imaginez le canal de distance constante que vous sélectionnez comme une fenêtre mouvante qui s'arrête momentanément au-dessus de chaque entité pour l'observer dans le contexte de ses voisins. Voici quelques grandes lignes pour vous aider à identifier un canal de distance adéquat pour l'analyse :
- Sélectionnez une distance en vous appuyant sur vos connaissances de l'étendue géographique des processus spatiaux favorisant l'agrégation pour les phénomènes que vous étudiez. Souvent vous l'ignorez mais, si tel n'est pas le cas, appuyez-vous sur vos connaissances pour sélectionner une valeur de distance. Supposons, par exemple, que vous sachiez que la distance moyenne domicile-travail est 15 kilomètres. Utiliser 15 kilomètres comme canal distance constitue une bonne stratégie pour l'analyse des données de trajets.
- Utilisez un canal de distance suffisamment grand pour garantir que toutes les entités aient au moins un voisin, sinon les résultats ne seront pas valides. Surtout si les données en entrée sont asymétriques (à savoir, qu'elles ne créent pas une courbe en cloche lorsque les valeurs sont tracées sous la forme d'un histogramme), vous devez vous assurer que votre canal distance n'est ni trop petit (la plupart des entités ont seulement un ou deux voisins) ni trop grand (plusieurs entités comprennent toutes les autres entités comme voisins), car cela nuirait à la fiabilité des scores Z résultants. Les scores z sont fiables (même avec des données biaisées) tant que le canal de distance est suffisamment grand pour garantir plusieurs voisins (environ huit) pour chaque entité. Même si aucune des entités n'a toutes les autres entités comme voisins, vous risquez de rencontrer des problèmes de performances et même éventuellement de mémoire insuffisante si vous créez un canal de distance où les entités ont des milliers de voisins.
- En vous assurant que toutes les entités ont au moins un voisin, vous risquez d'obtenir des entités associées à des milliers de voisins, ce qui n'est pas souhaitable. Cela peut se produire si certaines de vos entités sont des points spatiaux aberrants. Pour résoudre ce problème, déterminez une valeur de canal de distance appropriée pour tous les points sauf les points spatiaux aberrants et utilisez l'outil Générer la matrice de pondérations spatiales pour créer un fichier de matrice de pondérations spatiales utilisant cette distance. Toutefois, lorsque vous exécutez l'outil Générer la matrice de pondérations spatiales, spécifiez une valeur minimale pour le paramètre Nombre de voisins. Supposons, par exemple, que vous évaluiez l'accès à une alimentation saine dans le comté de Los Angeles à l'aide des données des secteurs de recensement. Vous savez que plus de 90 pour cent de la population vit dans un rayon de trois kilomètres des commerces. En analysant les secteurs de recensement, vous constatez que la distance entre les secteurs (basée sur les centroïdes de ces derniers) dans le centre-ville est d'environ 1 000 mètres en moyenne, alors que dans les zones périphériques, cette distance est supérieure à 18 000 mètres. Pour garantir que chaque entité a au moins un voisin, votre canal de distance devrait être supérieur à 18 000 mètres, et cette échelle d'analyse (distance) n'est pas adaptée aux questions que vous posez. La solution consiste à créer un fichier de matrice de pondérations spatiales pour la classe d'entités des secteurs de recensement à l'aide de l'outil Générer la matrice de pondérations spatiales. Spécifiez 4 800 mètres comme valeur du paramètre Distance seuil et une valeur minimale (2, par exemple) pour le paramètre Nombre de voisins. Cela appliquera une distance de voisinage fixe de 4 800 mètres à toutes les entités sauf à celles qui n'ont pas au moins deux voisins en utilisant cette distance. Pour les entités aberrantes (et pour elles seulement), la distance sera augmentée juste assez pour garantir que chacune d'elles a au moins deux voisins.
- Utilisez un canal distance qui reflète l'auto-corrélation spatiale maximale. Dès lors que vous remarquez une agrégation spatiale dans le paysage, vous voyez la preuve de l'existence de processus spatiaux sous-jacents. Le canal de distance qui présente l'agrégation maximale, mesurée par l'outil Autocorrélation spatiale incrémentielle, est la distance où ces processus spatiaux sont les plus actifs ou prononcés. Exécutez l'outil Autocorrélation spatiale incrémentielles et notez où les scores z obtenus semblent atteindre un pic. Utilisez la distance associée à la valeur pic pour l'analyse.
Remarque :
Indiquez les valeurs de distance avec les mêmes unités que celles spécifiées par le système de coordonnées en sortie de l'environnement de géotraitement.
- Chaque pic représente une distance où les processus qui favorisent l'agrégation spatiales sont les plus prononcés. Les pics multiples sont courants. En général, les pics associés aux plus grandes distances reflètent des tendances générales (une tendance générale d'est en ouest, par exemple, où l'ouest est un hot spot géant et l'est, un cold spot géant). Vous vous intéresserez normalement le plus aux pics associés aux plus petites distances ; il s'agit souvent du premier.
- Un petit pic signifie souvent que plusieurs processus spatiaux différents sont en cours à diverses échelles spatiales. Vous souhaiterez probablement rechercher d'autres critères pour déterminer la distance constante à utiliser pour l'analyse (peut-être la distance la plus efficace pour la remédiation).
- Si le score z ne présente jamais de pics (en d'autres termes, qu'il ne cesse d'augmenter) et si vous utilisez des données agrégées (par exemple, des comtés), cela signifie généralement que le schéma d'agrégation est trop grossier ; les processus spatiaux dignes d'intérêt fonctionnent à une échelle plus petit que celle des unités d'agrégation. Si vous pouvez passer à une échelle d'analyse plus réduite (de comtés à des secteurs, par exemple), cela pourrait aider à trouver un pic de distance. Si vous travaillez sur des données ponctuelles et si les scores z ne présentent jamais de pics, c'est qu'il existe de nombreux processus spatiaux différents fonctionnant à diverses échelles spatiales et vous devrez probablement trouver des critères différents pour déterminer la distance constante à utiliser dans votre analyse. Lorsque vous utilisez l'outil Autocorrélation spatiale incrémentielle, vérifiez si la valeur du paramètre Distance de départ n'est pas trop élevée.
- Si vous ne spécifiez pas de distance de départ, l'outil Autocorrélation spatiale incrémentielle utilise la distance permettant d'assurer que toutes les entités ont au moins un voisin. Si vos données incluent des points spatiaux aberrants, cette distance risque cependant d'être trop élevée pour votre analyse et peut être la raison de l'absence de pic prononcé dans le Fichier de rapport en sortie. Pour remédier à ce problème, exécutez l'outil Autocorrélation spatiale incrémentielle sur un jeu de sélection excluant temporairement tout les points spatiaux aberrants. Si, lorsque les points aberrants sont exclus, vous trouvez un pic, utilisez la stratégie détaillée ci-dessus avec ce pic de distance appliqué à toutes vos entités (points aberrants spatiaux inclus) et forcez chaque entité à avoir au moins un ou deux voisins. Si vous ne savez pas si certaines de vos entités sont des points aberrants spatiaux:
- Pour les données surfaciques, effectuez le rendu des surfaces de polygone à l'aide d'un schéma de rendu d'écart type et considérez les polygones dont les surfaces sont supérieures à trois écarts type comme étant des points aberrants spatiaux. Vous pouvez utiliser l'option Calculer un champ pour créer un champ avec des surfaces de polygones si vous n'en n'avez pas déjà un.
- Pour les données ponctuelles, utilisez l'outil Proche pour calculer la distance du voisin le plus proche pour chaque entité. Pour ce faire, définissez votre jeu de données ponctuelles comme valeur des paramètres Entités en entrée et Entités de proximité. Une fois que vous disposez d'un champ avec des distances de voisin le plus proche, représentez ces valeurs à l'aide d'un schéma de rendu d'écart type et considérez les distances qui sont supérieures à trois écarts type comme étant des points aberrants spatiaux.
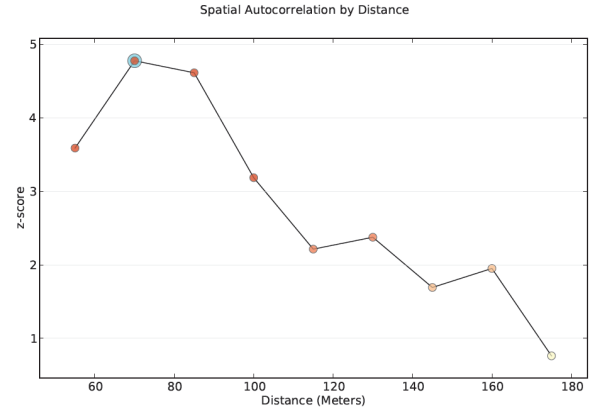
Identifier une distance où les processus qui favorisent l'agrégation sont les plus prononcés. - Essayez de ne pas vous focaliser sur l'idée qu'il existe un seul canal de distance correct. La réalité n'est jamais aussi simple. Il existe très probablement des processus spatiaux multiples/en interaction qui favorisent l'agrégation observée. Plutôt que de penser que vous avez besoin d'un canal de distance, envisagez les outils d'analyse de modèles comme des méthodes efficaces d'exploration des relations spatiales à diverses échelles spatiales. Pensez que, lorsque vous changez d'échelle (que vous changez la valeur de canal de distance), vous pouvez poser une question différente. Supposons que vous examiniez des données relatives aux revenus. Si vous avez des canaux de distance réduits, vous pouvez examiner des modèles de revenus de quartier, des distances d'échelle moyennes peuvent refléter les modèles de revenus au sein d'une communauté ou d'une ville, et les canaux de distance plus importants mettent en avant des modèles de revenus régionaux.
Méthode de distance
Nombre des outils de la boîte à outils Spatial Statistics utilisent la distance dans leurs calculs. Ces outils vous donnent le choix entre distance euclidienne ou de Manhattan.
- La distance euclidienne est calculée de la manière suivante
D = sq root [(x1–x2)**2.0 + (y1–y2)**2.0]où (x1,y1) est la coordonnée du point A, (x2,y2) la coordonnée du point B et D la distance en ligne droite entre les points A et B.

- La distance de Manhattan est calculée de la manière suivante
D = abs(x1–x2) + abs(y1–y2)où (x1,y1) est la coordonnée du point A, (x2,y2) la coordonnée du point B et D est la différence verticale plus horizontale entre les points A et B. Il s'agit de la distance que vous devez parcourir si vous êtes limité aux déplacements nord-sud et est-ouest. Cette méthode est généralement plus appropriée que la distance euclidienne lorsque le trajet est limité à un réseau de rues et si les coûts de déplacement dans le réseau de rues ne sont pas disponibles.

Si vos entités en entrée ne sont pas projetées (c'est-à-dire si elles ne sont pas exprimées en degrés, minutes et seconds) ou si le système de coordonnées en sortie est défini comme étant un système de coordonnées géographiques ou lorsque vous précisez un chemin de classe d'entités en sortie vers un jeu de données d'entités doté d'une référence spatiale de système de coordonnées géographiques, les distances sont calculées à l'aide des mesures à la corde et le paramètre Méthode de calcul de distance est désactivé. Les mesures de distance à la corde permettent de calculer rapidement et de fournir une bonne estimation de distance géodésiques réelles, du moins pour les points situés à environ trente degrés les uns des autres. Les distances à la corde s'appuient sur une sphère plutôt que sur la véritable forme d'ellipsoïde aplati de la Terre. Si l'on prend deux points sur la surface de la Terre, la distance à la corde qui les sépare est la longueur d'une ligne qui traverse la Terre en trois dimensions pour relier ces deux points. Les distances à la corde sont exprimées en mètres. Veillez à projeter les données si votre zone d'étude s'étend au-delà de 30 degrés. Les distances à la corde ne constituent pas une bonne estimation des distance géodésiques au-delà de 30 degrés.Attention :
Potentiel propre (champ donnant une pondération intra-zonale)
Plusieurs outils de la boîte à outils Spatial Statistics permettent de fournir un champ représentant la pondération à utiliser pour le potentiel propre. Le potentiel propre représente la distance ou la pondération entre une entité et elle-même. Cette pondération est souvent égale à zéro, mais, dans certains cas, il se peut que vous deviez spécifier une autre valeur fixe ou une valeur différente pour chaque entité. Si votre conceptualisation de relations spatiales s'appuie sur les distances parcourues dans et entre des secteurs de recensement, par exemple, vous pouvez décider de modéliser le potentiel propre afin de refléter les coûts de déplacement intra-zonaux d'après la taille du polygone :
dii = 0.5*[(Ai / π)**0.5]où dii est le coût de déplacement associé au déplacement intra-zonal pour les entités surfaciquesiet Ai la zone associée à l'entité surfaciquei.
Standardisation
La standardisation par lignes est recommandée chaque fois que la répartition de vos entités est potentiellement influencée par la conception de l'échantillonnage ou un plan d'agrégation imposé. Lorsque la standardisation par lignes est sélectionnée, chaque pondération est divisée par la somme des lignes (la somme des pondérations de toutes les entités voisines). La pondération standardisée de lignes est souvent utilisée avec des voisinages de distance constante et presque toujours utilisée pour les voisinages d'après la contiguïté des polygones. Cela permet de réduire le biais occasionné par les entités possédant des nombres de voisins différents. La standardisation par ligne met à l'échelle toutes les pondérations, de sorte qu'elles se trouvent entre 0 et 1, et crée une structure de pondération relative, plutôt qu'absolue. Chaque fois que vous travaillez avec des entités surfaciques représentant des limites administratives, vous souhaiterez probablement sélectionner l'option Standardisation par lignes.
Exemples:
- Supposons que vous disposiez d'un ensemble complet de tous les délits. Certaines parties de votre zone d'étude comprennent un grand nombre de points, car il s'agit des endroits où la criminalité est élevée. D'autres comprennent peu de points, car la criminalité y est faible. La densité des points reflète correctement ce que vous essayez de comprendre : la distribution spatiale de la criminalité. Vous n'utiliserez probablement pas la standardisation par lignes pour vos pondérations spatiales.
- Supposons que vous ayez collecté des échantillons de sol. Pour une raison indéterminée (il faisait beau, ou bien vous étiez dans un endroit où vous n'avez pas eu à escalader de clôture, à traverser un marécage ou à gravir une montagne), vous avez beaucoup d'échantillons pour certaines parties de la zone d'étude, et moins pour d'autres. En d'autres termes, la densité des points n'est pas strictement le résultat d'un échantillon aléatoire préparé avec soin. Certaines de vos préconceptions ont pu être introduites. En outre, les endroits comportant plus de points ne reflètent pas nécessairement la distribution spatiale sous-jacente des données que vous analysez. Pour minimiser les biais qui peuvent avoir été introduits au cours du processus d'échantillonnage, vous devrez soumettre vos pondérations spatiales à la standardisation par lignes. Lorsque vous procédez à une standardisation par lignes, le fait qu'une entité ait 2 voisins et qu'une autre en ait 18 a peu d'effet sur les résultats. La somme des pondérations est égale à 1.
- Lorsque que vous agrégez vos données, vous leur imposez une structure. Cette structure reflète rarement correctement les données que vous analysez et les questions que vous posez. Par exemple, alors que les polygones de recensement (comme les secteurs de recensement) sont applicables à la population, même si votre analyse implique des questions relatives à la population, il vous faudra probablement procéder à une standardisation par lignes de vos pondérations car ces polygones constituent seulement une des nombreuses façons de représenter ces dernières. Pour les données surfaciques, vous devrez pratiquement toujours effectuer la standardisation par lignes des pondérations spatiales.
Canal distance ou distance seuil
Canal distance ou distance seuil définit l'échelle d'analyse de la plupart des conceptualisations de relations spatiales (par exemple, INVERSE_DISTANCE et FIXED_DISTANCE_BAND). Il s'agit d'une valeur numérique positive représentant une distance limite. Les entités se trouvant à l'extérieur de la limite spécifiée pour une entité cible ne sont pas prises en compte dans l'analyse pour cette entité. Cependant, avec ZONE_OF_INDIFFERENCE, l'influence des entités situées hors de la distance donnée est réduite par rapport à la proximité, tandis que les entités se trouvant dans le seuil de distance sont considérées à part égale.
Il est important de choisir une distance appropriée. Certaines statistiques spatiales nécessitent que chaque entité ait au moins un voisin pour que l'analyse soit fiable. SI la valeur que vous définissez pour Canal distance ou distance seuil est trop petite (et que certaines entités n'ont pas de voisins), un message d'avertissement indique que vous devez essayer à nouveau avec une valeur de distance plus importante. L'outil Calculer la bande de distance à partir du nombre de voisins évalue les distances minimale, maximale et moyenne pour un nombre spécifié de voisins et peut vous aider à déterminer une valeur de canal distance adéquate à utiliser pour l'analyse. Consultez la rubrique Sélection d'une valeur de canal distance constante pour plus d'indications.
Si aucune valeur n'est spécifiée, une distance seuil par défaut est calculée. Le tableau ci-après indique la façon dont les différentes valeurs du paramètre Conceptualisation de relations spatiales se comportent pour chacun des trois types d'entrée possibles (les valeurs négatives ne sont pas valides) :
| Inverse de la distance, Inverse de la distance au carré | Canal distance constante, Zone d'indifférence | Contiguïté polygonale, Triangulation de Delaunay, K voisins les plus proches | |
| 0 | Aucun seuil ni limite n'est appliqué, toutes les entités sont des voisins de toutes les autres entités. | Non valide. Une erreur d'exécution est générée. | Ignoré. |
| vierge | Une distance par défaut est calculée. Cette valeur est la distance minimale qui permet de s'assurer que chaque entité possède au moins un voisin. | Une distance par défaut est calculée. Cette valeur est la distance minimale qui permet de s'assurer que chaque entité possède au moins un voisin. | Ignoré. |
| nombre positif | La valeur positive, non zéro, spécifiée est utilisée comme distance limite, les relations de voisinage existent uniquement parmi les entités au sein de cette distance les unes par rapport aux autres. | Dans le cas du canal de distance constante, seules les entités qui se trouvent dans cette limite spécifiée les unes par rapport aux autres sont voisines. Dans le cas de la zone d'indifférence, les entités au sein de cette limite spécifiée les unes par rapport aux autres sont voisines, ainsi que celles situées en-dehors de la limite, mais celles-ci ont une pondération/influence qui diminue à mesure que la distance augmente. | Ignoré. |
Nombre de voisins
Spécifiez un nombre entier positif pour représenter le nombre de voisins à inclure dans l'analyse de chaque entité cible. Lorsque la valeur choisie pour le paramètre Conceptualisation de relations spatiales est K voisins les plus proches, chaque entité cible est évaluée dans le contexte des K entités les plus proches (où K est le nombre de voisins spécifié). Pour le paramètre Distance inverse ou Canal de distance constante, lorsque vous exécutez l'outil Générer la matrice de pondérations spatiales, spécifiez une valeur pour le paramètre Nombre de voisins pour que chaque entité ait un minimum de K voisins. Pour la méthode de contiguïté polygonale, les entités pour lesquelles le paramètre Nombre de voisins n'est pas spécifié se voient attribuer des voisins supplémentaires en fonction de la proximité des centroïdes des entités. Pour l'outil Générer les pondérations spatiales de réseau, spécifiez une valeur pour le paramètre Nombre de voisins maximal afin qu'aucune entité n'ait davantage de voisins que la valeur spécifiée. Pour l'outil Analyse des regroupements, spécifiez une valeur pour le paramètre Nombre de voisins afin d'encourager la proximité des entités dans chaque groupe. En spécifiant 6 voisins, par exemple, vous limitez les groupes à des entités partageant au moins un des six voisins les plus proches avec d'autres entités du groupe.
Fichier de matrice de pondérations
Plusieurs outils permettent de définir des relations spatiales entre entités en fournissant un chemin vers un fichier de matrice de pondérations spatiales. Les pondérations spatiales sont des nombres qui reflètent la distance, l'heure ou d'autres coûts entre toutes les entités dans le jeu de données. Vous pouvez créer le fichier de matrice de pondérations spatiales à l'aide de l'outil Générer la matrice de pondérations spatiales ou Générer les pondérations spatiales de réseau ou il peut s'agir d'un simple fichier ASCII.
Lorsque le fichier de matrice de pondérations spatiales est un simple fichier de texte ASCII, la première ligne doit être le nom d'un champ d'ID unique. Cela vous permet d'utiliser tout champ numérique dans votre jeu de données comme ID lors de la génération de ce fichier. Cependant, ce champ doit être de type entier (long ou court) et contenir des valeurs uniques pour chaque entité. Après la première ligne, le fichier de pondérations spatiales doit contenir trois colonnes :
- ID d'entité de départ
- ID d'entité d'arrivée
- Poids
Supposons, par exemple, que vous ayez trois stations service. Le champ que vous utilisez comme champ d'ID est StationID et les ID d'entités sont 1, 2 et 3. Vous souhaitez modéliser les relations spatiales entre ces trois stations service grâce au temps de trajet en minutes. Vous pouvez créer un fichier ASCII comme celui-ci :

En général, lorsque des pondérations représentent une distance ou une durée, elles sont inversées (par exemple 1/10 lorsque la distance est 10 km ou 10 minutes), afin que les entités plus proches aient une pondération supérieure aux entités plus éloignées. Vous remarquerez que les pondérations au-dessus de celles de la station service 1 sont à 10 minutes de la station 2. Le temps de trajet n'est pas symétrique dans cet exemple (le trajet de la station 1 à la 3 est de 7 minutes, mais celui de la station 3 à la 1 est de seulement 6 minutes). Remarquez que la pondération entre la station service 1 et elle-même est 0 et qu'il n'existe aucune entrée pour la station 2 par rapport à elle-même. Les entrées manquantes sont supposées avoir une pondération égale à 0.
La saisie de valeurs pour la matrice de pondérations spatiales peut être une tâche fastidieuse, même pour de petits jeux de données. Il est préférable de faire appel à l'outil Générer la matrice de pondérations spatiales ou d'écrire un script Python qui se chargera de cette tâche.
Fichier matrice de pondérations spatiales (.swm)
Les outils Générer la matrice de pondérations spatiales et Générer les pondérations spatiales de réseau créent un fichier de matrice de pondérations spatiales (.swm) qui définit les relations spatiales entre toutes les entités de votre jeu de données en fonction des paramètres que vous spécifiez. Ce fichier est créé en format binaire afin que les valeurs qu'il contient ne puissent pas être vues directement. Pour consulter ou modifier les relations entre entités dans un fichier SWM, utilisez l'outil Convertir la matrice de pondérations spatiales en table.
Si les relations spatiales entre entités sont stockées dans une table, vous pouvez utiliser l'outil Générer la matrice de pondérations spatiales pour convertir cette table en fichier de matrice de pondérations spatiales (.swm). La table a besoin des champs suivants :
| Nom du champ | Description |
|---|---|
| <Nom du champ d’ID unique> | Champ de nombre entier qui existe dans la classe d'entités en entrée avec un ID unique pour chaque entité. il s'agit de l'ID d'entité de départ. |
| NID | Champ d'entier contenant les ID des entités voisines. Il s'agit de l'ID d'entité d'arrivée. |
| POIDS | C'est la pondération numérique quantifiant la relation spatiale entre les entités de départ et d'arrivée. Les valeurs élevées représentent des pondérations plus importantes et une influence, ou interaction, plus forte entre deux entités. |
Partage de fichiers de matrice de pondérations spatiales
La sortie des outils Générer la matrice de pondérations spatiales et Générer les pondérations spatiales de réseau est un fichier SWM. Ce fichier est lié à la classe d'entités en entrée, au champ d'ID unique et aux paramètres du système de coordonnées en sortie lors de la création du fichier SWM. D'autres personnes peuvent dupliquer les relations spatiales que vous définissez pour l'analyse à l'aide de votre fichier SWM et de la même classe d'entités en entrée ou d'une classe d'entités liant toutes les entités (ou un sous-ensemble de celles-ci) à un champ d'ID unique identique. Essayez d'éviter que votre système de coordonnées en sortie ne diffère de la référence spatiale associée à votre classe d'entités en entrée, particulièrement si vous projetez de partager vos fichiers SWM. Une meilleure stratégie consiste à projeter la classe d’entités en entrée, puis à définir le système de coordonnées en sortie comme étant le même que celui de la classe d'entités en entrée avant de créer les fichiers de matrice de pondérations spatiales.