La puissance de l'outil Trier réside dans sa capacité à trier les entités spatialement. Un tri spatial permet d'améliorer l'efficacité des opérations géométriques et spatiales.
Pour trier des entités spatialement (à savoir, par emplacement), sélectionnez Forme dans le paramètre Champ(s). En sélectionnant le champ Shape, vous activez le paramètre Méthode de tri spatial avec cinq options déroulantes qui vous permettent de définir l'algorithme de tri. Les options sont UL, UR, LL, LR et PEANO.
Tri spatial à l'aide des options UL, UR, LL, LR
Les quatre premières options sont les abréviations du point de départ du tri : par exemple, UR pour supérieur droit et LR pour inférieur gauche. Ces options permettent de numériser les entités comme le ferait un traceur ou une imprimante. Si vous choisissez l'option UR, la numérisation commence dans le coin supérieur droit et l'entité supérieure est la première sélectionnée. Pour un tri du haut vers le bas, si au moins deux entités se trouvent sur la même ligne horizontale, elles sont classées de droite à gauche. La numérisation se poursuit vers le bas et vers la gauche jusqu'au coin opposé (inférieur gauche dans ce cas). Les entités sont triées dans l'ordre (ou dans l'ordre opposé, si vous sélectionnez DESCENDING) dans lequel elles sont numérisées ou sollicitées.
L'option de tri UR peut être illustrée sans peine en utilisant un ensemble de points distribué uniformément en entrée.
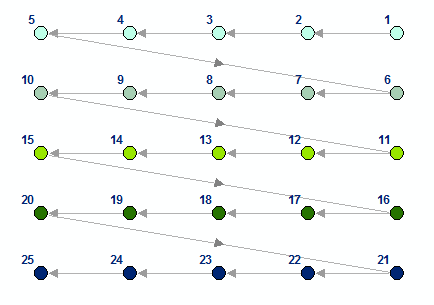
Les numéros du diagramme ci-dessus représentent la séquence triée avec l'option UR. L'ordre des entités est inversé si vous sélectionnez l'option LL.
Voici un exemple simple illustrant l'interaction entre les points supérieurs et ceux qui se trouvent à droite.
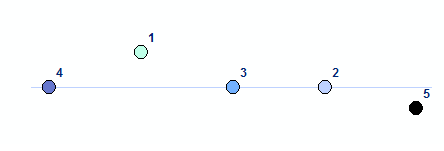
Vous pouvez remarquer que U a priorité sur R. R est pris en compte uniquement lorsque certaines entités se trouvent au même niveau horizontal.
Tri spatial en fonction de l'option PEANO
L'option PEANO utilise l'algorithme de la courbe Peano. L'algorithme explore tous les emplacements d'un voisinage limité d'abord avant de passer au voisinage suivant. Ainsi, les emplacements voisins sont plus proches le long de la courbe (ou de la trajectoire). Plutôt que d'explorer l'étendue entière, elle explore les plus petits voisinages un par un, puis après avoir traité une surface étendue (de 5 à 8 voisinages plus petits), elle passe à une autre surface plus étendue et redémarre le tri à partir d'un petit voisinage de cette surface plus étendue.
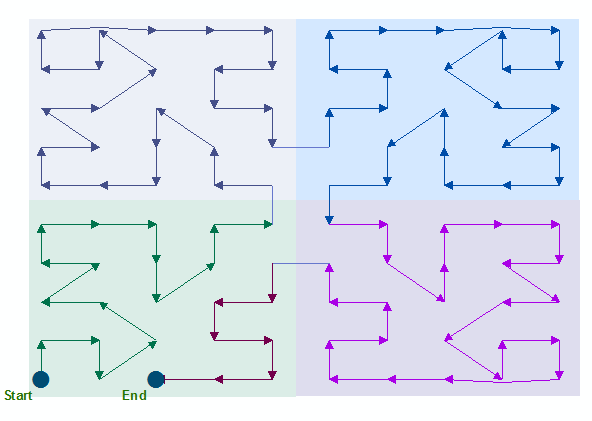
Dans le diagramme ci-dessus, la séquence de numérisation est indiquée par des flèches. Chacun des quatre voisinages rectangulaires est numérisé séparément. Si la surface était plus importante, la recherche se poursuit sur un autre ensemble de voisinages, etc. Si les points étaient plus denses, l'exploration porterait sur un voisinage bien plus petit.
Les avantages d'un algorithme de courbe de remplissage d'espace sont les suivants : il est rapide et ne doit pas calculer les distances qui séparent les emplacements, puis il est parallélisable. Cet algorithme est appliqué pour résoudre le problème d'un voyageur de commerce, pour construire un système de calcul d'itinéraires et contrôler un traceur pour dessiner des cartes.