一般的に、統計的検証の最初の作業は、帰無仮説を確認することです。パターン分析ツール ([パターン分析] ツールセットと[クラスター分析のマッピング] ツールセット) の帰無仮説は、フィーチャそのもの、またはこれらのフィーチャに関連付けられている値の CSR (Complete Spatial Randomness: 空間完全ランダム性) です。パターン分析ツールによって返される Z スコアと p 値は、この帰無仮説を棄却できるかどうかを示します。一般的に、Z スコアと p 値に基づいて帰無仮説を却下しても問題がないことを確認するために、パターン分析ツールを実行します。これは、ランダムなパターンではなく、フィーチャ (またはこれらのフィーチャに関連付けられている値) が統計的に有意なクラスタリングまたは分散を示していることを意味するからです。地形 (または空間データ) にクラスタリングなどの空間構造がある場合、一定の内在する空間プロセスがアクティブであることが示されますが、これは通常、地理学者や GIS アナリストにとって最も重要な情報です。
p 値は、確率です。パターン分析ツールでは、これは、観測された空間パターンが一定のランダム プロセスによって作成された確率です。p 値が非常に小さければ、観測された空間パターンがランダム プロセスの結果である可能性が非常に低い (確率が小さい) ことを意味するため、帰無仮説を棄却できます。ここで、値が小さいと判断するための基準を知っておく必要があります。この重要な情報については、後で示す表と説明をご参照ください。
Z スコアは、標準偏差です。たとえば、ツールによって返された Z スコアが +2.5 であれば、標準偏差が 2.5 であることを示します。Z スコアと p 値は、次に示すように、標準正規分布に関連付けられます。
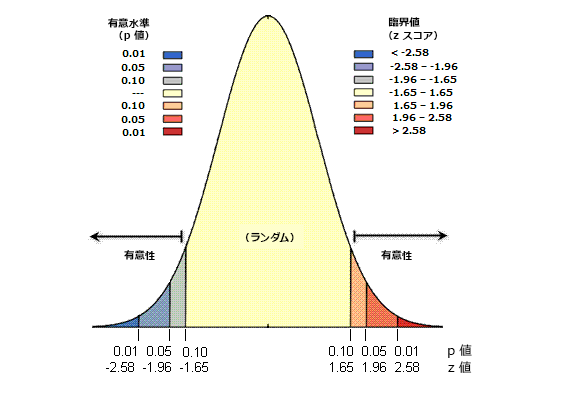
非常に小さい p 値に関連付けられている非常に高いまたは非常に低い (負) Z スコアが正規分布の尾部に見られます。フィーチャ パターン分析ツールを実行し、それが小さい p 値と非常に高いまたは非常に低い Z スコアを示した場合、これは観測された空間パターンが帰無仮説によって表される理論的なランダム パターン (CSR) を反映している可能性がほとんどないことを示します。
帰無仮説を棄却するためには、誤りである (帰無仮説を不当に棄却する) リスクをどれほど許容できるかを主観的に判断する必要があります。したがって、空間統計を実行する前に、信頼度を選択します。一般的に使用される信頼度は、90%、95%、または 99% です。99% の信頼度は、この場合、最も保守的であり、パターンがランダムな可能性によって作成された確率が非常に小さい (1% 未満) 場合を除き、帰無仮説を棄却しないことを示します。
信頼度
次の表は、補正されていない重要な p 値と Z スコアを信頼度別に示しています。
| Z スコア (標準偏差) | p 値 (確率) | 信頼度 |
|---|---|---|
< -1.65 または > +1.65 | < 0.10 | 90% |
< -1.96 または > +1.96 | < 0.05 | 95% |
< -2.58 または > +2.58 | < 0.01 | 99% |
ここで、1 つの例を検証します。95% の信頼度を使用する場合、重要な Z スコア値は標準偏差 -1.96 および +1.96 です。95% の信頼度に関連付けられている補正されていない p 値は 0.05 です。Z スコアが -1.96 と +1.96 の間にある場合、補正されていない p 値は 0.05 より大きくなり、帰無仮説を棄却できません。示されたパターンはランダムな空間プロセスの結果である可能性が非常に高いと考えられるからです。Z スコアがこの範囲外である場合 (たとえば、標準偏差が -2.5 や +5.4 である場合)、観測された空間パターンが特異すぎるため、ランダムな可能性の結果ではない可能性があり、p 値はこれを反映するために小さくなります。この場合、帰無仮説を棄却して、統計的に有意な空間構造がデータ内で発生する原因の特定を進めることができます。
ここで重要な点は、正規分布の中央の値 (たとえば、Z スコアが 0.19 や -1.2 であること) が必要とされる結果を表すことです。Z スコアの絶対値が大きく、確率が小さい (正規分布の尾部にある) 場合は、特異で非常に重要な情報を示していることになります。たとえば、[ホット スポット分析 (Hot Spot Analysis (Getis-Ord Gi*))] ツールの場合、統計的に有意なホット スポットまたは統計的に有意なコールド スポットが存在することが「特異」な状態です。
FDR 補正
[ホット スポット分析 (Hot Spot Analysis)] および[クラスター/外れ値分析 (Cluster and Outlier Analysis (Anselin Local Morans I))] を含むローカル空間パターン解析ツールは、ブール型のパラメーター [False Discovery Rate (FDR) 補正] をオプションで提供します。このパラメーターをオンにすると、FDR (False Discovery Rate) は、多重検定および空間依存性を考慮できるように上の表 の重要な p 値の閾値を小さくできる場合があります。値を小さくできた場合、その減少分は、入力フィーチャおよび使用されている近傍構造の数の関数になります。
ローカル空間パターン解析ツールは、隣接するフィーチャのコンテキスト内で各フィーチャを検討し、ローカル パターン (ターゲット フィーチャおよびその近傍) が統計的にグローバル パターン (データセットのすべてのフィーチャ) と異なるかどうかを判定する仕組みになっています。各フィーチャに関連付けられている Z スコアおよび p 値の結果から、その差異が統計的に有意であるかどうかが判定されます。この分析的なアプローチは、多重検定および依存性の両方を含む問題を引き起こします。
多重検定- 確率理論により、95% の信頼度では、100 回中 5 回の確率で、空間パターンが構造化 (クラスタリング、分散化など) されたり、統計的に有意な p 値に関連付けられることがわかっています。実際には、そのパターンを促進している、基となっている空間処理は真にランダムです。これらのケースでは、p 値が統計的に有意であるために、誤って CSR 帰無仮説を却下してしまいます。100 回中 5 回というのは、ローカル空間統計でデータセットのすべてのフィーチャに検定を行うことを念頭に入れているのであれば、極めて保守的に思えます。たとえば、フィーチャ が 10,000 ある場合、500 の間違った結果を得る可能性があります。
空間依存性- 互いに近い距離にあるフィーチャ同士は、空間データが空間的な依存性を示していないフィーチャに比べると類似する傾向にあります。それにもかかわらず、多くの統計的な検定では、フィーチャが独立している必要があります。ローカル パターン解析ツールの場合、空間依存性によって統計的な有意性が人工的に誇張される可能性があるからです。各フィーチャはその近傍のコンテキスト内で評価され、互いの距離が近いフィーチャは、同じ近傍のフィーチャを共有する可能性が高くなるため、ローカル パターン解析ツールを使用すると空間依存性に悪影響があります。このオーバーラップは、空間依存性を強調します。
多重検定および空間依存性のいずれの問題にも対処できるアプローチは 3 つ以上あります。最初のアプローチは、その問題を無視することです。データセットの各フィーチャに実行される個別の検定は分離して検討する必要があるからです。ただし、このアプローチでは、一部の統計的に有意な結果が誤判定される可能性が高くなります (基となっている空間処理がランダムである場合は統計的に有意に見えます)。2 番目のアプローチは、Bonferroni または Sidak の補正法などのように古典的な多重検定のプロセスを適用することです。ただし、これらの方法は、一般的に保守的すぎます。これらの方法で誤判定の数を非常に少なくすることはできますが、これらが存在すると統計的に有意な結果を見逃すこともあります。3 番目のアプローチは、FDR 補正を適用することです。FDR 補正は、特定の信頼度における誤判定の数を推定し、それに基づいて重要な p 値を調整します。この方法では、統計的に有意な p 値は、最小 (最強) から最大 (最弱) までの順位が付けられ、誤判定の推定に基づいて最小をリストから削除します。統計的に有意な p 値を持つ残りのフィーチャは、出力フィーチャクラスの Gi_Bin または COType フィールドによって識別されます。この方法は、完璧とはいえないものの、経験に基づく検定から、ローカルの各検定が個別に実行されていることを前提としたり、従来のあまりにも保守的な多重検定方法を適用することに比べると、より信頼できる結果が得られることがわかっています。その他のリソース セクションでは、FDR 補正の詳細が説明されています。
帰無仮説および空間統計
[空間統計] ツールボックスのいくつかの統計 ([空間的自己相関分析 (Spatial Autocorrelation (Global Moran's I))]、[クラスター/外れ値分析 (Cluster and Outlier Analysis (Anselin Local Moran's I))]、および [ホット スポット分析 (Hot Spot Analysis (Getis-Ord Gi*))] など) は、推定的な空間パターン分析手法です。推定的な統計は、確率理論に基づいています。確率は、可能性を計測するための基準であり、基になるすべての統計テストは (直接的または間接的に)、分析の結果に見られる可能性の役割を評価する確率の算出を行うものです。通常、従来の (非空間的な) 統計では、ランダムなサンプルを使用して、サンプル データが母集団全体を適切に表現 (反映) している確率の特定が試みられます。たとえば、出口調査の結果 (候補者 A が候補者 B に僅差で当選することを示す) が選挙の最終結果を反映する可能性を調べる必要がある場合があります。しかし、上記の空間的自己相関タイプの統計を含む多くの空間統計では、スタディ エリアについて使用可能なすべてのデータ (すべての犯罪、すべての感染症ケース、すべての国勢調査区域の属性など) を処理することがよくあります。母集団全体の統計を計算する場合、推定は一切ありません。事実があるのみです。したがって、可能性または確率を考慮する意味がなくなります。スタディ エリアのすべてのデータに適用されることがよくある空間パターン解析ツールは、確率を正当に報告することもできます。そのためには、これらのツールは、帰無仮説を通じて、データは実際には一定のより大きい母集団の一部であると想定します。これについて、より詳細に説明します。
ランダム化帰無仮説 - [空間統計] ツールボックスのツールは、必要に応じて、統計的な有意性のテストの基盤としてランダム化帰無仮説を使用します。ランダム化帰無仮説は、観測されたデータの空間パターンは多くの (n!) 考えられる空間的配置の 1 つを表すと想定します。データ値を取得してスタディ エリアのフィーチャに適用すると、これらの値の 1 つの考えられる空間的配置となります (データ値を取得して任意に適用することは、ランダムな空間プロセスの 1 つの例です)。ランダム化帰無仮説は、この操作 (取得して適用) を無限に実行できる場合は、一般的に、観測されたパターン (実際のデータ) と著しく異ならないパターンが生成されることを示します。まったくの偶然でスタディ エリアの一部分にすべての最高値を適用することがありますが、それはまれです。ランダム化帰無仮説は、データが多数の考えられるバージョンの空間完全ランダム性の 1 つであることを示します。データ値は固定されており、その空間的配置のみが変化します。
正規化帰無仮説 - 広く使用されている派生帰無仮説は、正規化帰無仮説です。これは [空間統計] ツールボックスに実装されていません。正規化帰無仮説は、観測値は一定のランダム サンプリング プロセスから得られた値の無限に大きい正規分布している母集団から派生すると想定します。異なるサンプルを使用すると、異なる値が得られますが、これらの値がより大きい分布を表すものとなることは十分に予想されます。正規化帰無仮説は、値が多数の考えられる値のサンプルの 1 つを表すことを示します。観測されたデータを正規のカーブに適合させ、値をその分布からランダムに選択してスタディ エリアに適用することができる場合は、一般的に、観測されたパターンまたは分布 (実際のデータ) と著しく異ならない値のパターンおよび分布が生成されます。正規化帰無仮説は、データとその配置が多数の考えられるランダム サンプルの 1 つであることを示します。データ値もその空間的配置も固定されていません。正規化帰無仮説は、データ値が正規分布している場合にのみ適切です。
参考資料
- Ebdon, David『Statistics in Geography』Blackwell、1985 年
- Mitchell, Andy『The Esri Guide to GIS Analysis, Volume 2』Esri Press、2005 年
- Goodchild, M.F., Spatial Autocorrelation.Catmog 47, Geo Books, 1986
- Caldas de Castro, Marcia, and Burton H. Singer.False Discovery Rate"Controlling the False Discovery Rate: A New Application to Account for Multiple and Dependent Test in Local Statistics of Spatial Association."Geographical Analysis38, pp 180-208, 2006.
関連トピック
- 高/低クラスター分析 (High/Low Clustering (Getis-Ord General G))
- 空間的自己相関分析 (Spatial Autocorrelation (Global Moran's I))
- クラスター/外れ値分析 (Cluster and Outlier Analysis (Anselin Local Moran's I))
- ホット スポット分析 (Hot Spot Analysis (Getis-Ord Gi*))
- 最小二乗法 (Ordinary Least Squares)
- 最適化ホット スポット分析 (Optimized Hot Spot Analysis)
- 時空間ホット スポット分析 (Emerging Hot Spot Analysis)