Доступно с лицензией Geostatistical Analyst.
Методы кригинга зависят от математических и статистических моделей. Добавление статистической модели, включающей вероятность, отличает методы кригинга от детерминированных методов, описанных в разделе Детерминированные методы пространственной интерполяции. В случае кригинга с интерполяцией связана некоторая вероятность, то есть статистическая модель не дает идеально точных проинтерполированных значений. Рассмотрим пример выборки измеренных значений содержания азота в поле. Очевидно, даже при большой выборке будет невозможно спрогнозировать точное значение содержания азота в неизмеренном местоположении. Поэтому нужно не только попытаться предсказать его, но и оценить ошибку интерполяции.
Методы кригинга основаны на понятии автокорреляции. Под корреляцией обычно понимают тенденцию к связанности двух типов переменных. Например, на фондовой бирже существует тенденция положительных изменений при более низких процентных ставках, поэтому говорят, что эти два параметра имеют отрицательную корреляцию. Однако фондовая биржа имеет положительную автокорреляцию, то есть она имеет корреляцию внутри себя самой. На фондовой бирже два значения будут более близки друг к другу, если их разделяет только один день, а не один год. Это связано с базовым принципом географии — чем ближе объекты, тем больше сходства между ними. Скорость ослабления корреляции можно выразить в виде функции расстояния.
Автокорреляция — это функция расстояния. Это определяющее свойство геостатистики. В классической статистике наблюдения предполагаются независимыми, то есть между ними нет корреляции. В геостатистике информация по пространственным местоположениям позволяет вычислять расстояния между точками наблюдения и моделировать автокорреляцию как функцию расстояния.
Также следует отметить, что в общем случае стоимость фондового рынка растет со временем, и это называется трендом. Для геостатистических данных используются те же термины, и они выражаются следующей простой математической формулой:
Z(s) = µ(s) + ε(s),где Z(s) — искомая переменная, которая раскладывается на детерминированный тренд µ(s) и функцию случайных автокоррелированных ошибок ε(s). Символ s указывает местоположение; можно считать это совокупностью пространственных координат x (долгота) и y (широта). Варианты этой формулы составляют основу всех различных типов кригинга. Начните справа и двигайтесь влево.
Сложность тренда в модели не имеет значения, прогноз µ(s) все равно будет неидеален. В этом случае вводится ряд допущений относительно ошибок ε(s); а именно, предполагается, что они равны 0 (в среднем) и что автокорреляция между ε(s) и ε(s + h) не зависит от фактического местоположения s, а зависит только от относительного смещения h между ними. Это необходимо для репликации, чтобы можно было оценить функцию автокорреляции. Например, на следующем рисунке:
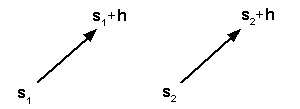
предполагается, что случайные ошибки в парах местоположений, соединенных стрелками, имеют одинаковую автокорреляцию.
Далее рассмотрим тренд. Это может быть простая константа, то есть µ(s) = m для всех местоположений s, и, если µ неизвестно, это модель, на которой основан обычный кригинг. Тренд может также представлять собой линейную функцию самих пространственных координат, например:
µ(s) = ß0 + ß1x + ß2y + ß3x2 + ß4y2 + ß5xy,Это полиномиальная поверхность тренда второго порядка и линейная регрессия для пространственных координат x и y. Меняющиеся тренды с неизвестными коэффициентами регрессии составляют модели для универсального кригинга. Если тренд полностью известен (то есть известны все параметры и независимые переменные), то независимо от того, является ли он константой, такой тренд составляет модель для простого кригинга.
Теперь рассмотрим левую часть декомпозиции, Z(s) = µ(s) + ε(s). Можно выполнить преобразования над Z(s). Например, можно заменить этот компонент индикаторной переменной, которая равна нулю, если Z(s) ниже определенного значения (например, 0,12 миллионной доли для концентрации озона), и единице, если Z(<b>s</b>) выше определенного значения. Можно предсказать вероятность того, что Z(s) превышает пороговое значение, и интерполяции по такой модели служат основой для индикаторного кригинга. Можно выполнить общие произвольные преобразования Z(s) и обозначить их fi(Z(si)) для i-й переменной. Можно составить предикторы из функций переменных; например, чтобы сделать прогноз в местоположении s0, нужно создать предиктор дизъюнктивного кригинга g(Z(s0)) с использованием данных fi(Z(si)).
Наконец, рассмотрим случай нескольких типов переменных, когда создаются модели Zj(s) = µj(s) + εj(s) для j-го типа переменной. Здесь можно считать, что для каждой переменной существует отдельный тренд и, помимо автокорреляции для ошибок εj(s), имеется также взаимная корреляция между ошибками εj(s) и εk(s) для двух типов переменных. Например, рассмотрим взаимную корреляцию между двумя переменными, такими как концентрации озона и твердых примесей, которые не обязательно измерять в одних и тех же точках. Модели, использующие несколько искомых переменных, составляют основу кокригинга. Можно создать индикаторную переменную Z(s); тогда при прогнозировании ее значения с использованием исходных непреобразованных данных Z(s) в модели кокригинга получим вероятностный кригинг. В случае нескольких искомых переменных можно рассматривать обычный, универсальный, простой, индикаторный, вероятностный и дизъюнктивный типы кокригинга в качестве многомерных расширений разных типов кригинга, описанных ранее.
Отзыв по этому разделу?