Краткая информация
Инструмент Исследовательская регрессия оценивает все возможные комбинации входных потенциальных независимых переменных, выполняя поиск моделей OLS, которые наилучшим образом описывают зависимую переменную в контексте критериев, заданных пользователем.
Доступ к результатам этого инструмента (в том числе дополнительному PDF-файлу отчета) можно получить в окне Результаты (Results). Если отключить фоновую обработку, результаты также будут показаны в диалоговом окне Ход процесса (Progress).
Более подробно о работе инструмента Исследовательская регрессия
Иллюстрация
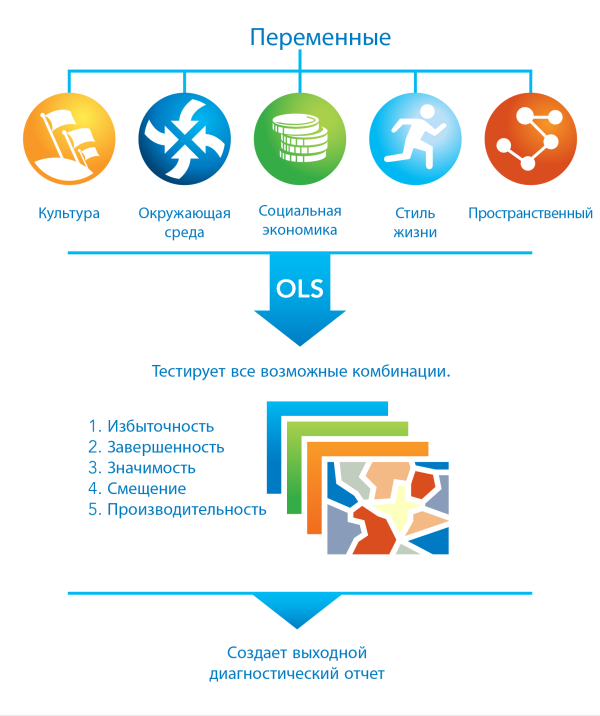
Использование
-
Основным результатом работы этого инструмента является файл отчета, который записывается в окне Результаты (Results). Если щелкнуть правой кнопкой мыши запись Сообщения в окне Результаты и выбрать Вид, итоговый отчет инструмента Исследовательская регрессия можно будет просмотреть в диалоговом окне Сообщение.
Этот инструмент при необходимости создает текстовый файл отчета со сводным представлением результатов. Файл отчета добавляется в таблицу содержания и его можно просмотреть в ArcMap, щелкнув его правой кнопкой и выбрав пункт Открыть.
Данный инструмент также формирует дополнительную таблицу всех моделей, соответствующих максимальному предельному p-значению коэффициента и заданному значению Фактора увеличения дисперсии (ФУД). Полное пояснение по каждому элементу отчета и таблицы представлено в разделе Интерпретации результатов выполнения инструмента Исследовательская регрессия.
Этот инструмент использует методы Наименьших квадратов (Ordinary Least Squares) (МНК) и Пространственная автокорреляция (Глобальный индекс Морана I) . Дополнительный файл пространственной матрицы весов используется с инструментом Пространственная автокорреляция (Глобальный индекс Морана I) для оценки невязок модели. Он совсем не применяется с инструментом OLS.
Этот инструмент использует каждую комбинацию возможных независимых значений для поиска правильной модели OLS. Когда он обнаруживает модель, соответствующую критериям Минимальный допустимый скорректированный коэффициент детерминации (Minimum Acceptable Adj R Squared), Максимальный порог p-значения коэффициента (Maximum Coefficient p-value Cutoff), Максимальный порог значения VIF (Maximum VIF Value Cutoff) и Минимально допустимое p-значение Жака-Бера (Minimum Acceptable Jarque-Bera p-value), запускается инструмент Пространственная автокорреляция (Глобальный индекс Морана I) с невязками модели, чтобы узнать, кластеризованы ли недооценки и переоценки. Чтобы предоставить хотя бы какую-нибудь информацию о кластеризации отклонений, если ни одна из моделей не соответствует этим критериям, тест Пространственная автокорреляция (Глобальный индекс Морана I) также применяется к невязкам для трех моделей с наибольшими скорректированными значениями R2 и трем моделям с наибольшими p-значениями Жака-Бера.
Если в зависимой переменной присутствует пространственная структура, следует использовать максимально возможное количество независимых переменных. К примерам пространственных переменных можно отнести расстояние до основных автострад, доступность вакансий, число близлежащих магазинов, измерения связности и плотности. Пока вы не найдете независимые переменные, которые эффективно опишут структуру ваших данных, невязки модели, скорее всего, не смогут пройти тест пространственной автокорреляции. Значительная кластеризация в невязках регрессии, определенная инструментом Пространственная автокорреляция (Глобальный индекс Морана I) , указывает на некорректность модели. Стратегии для обработки неправильно определенной модели см. в разделе Что вам не говорят о регрессионном анализе.
Так как инструмент Пространственная автокорреляция (Глобальный индекс Морана I) не запускается для всех тестируемых моделей (см. предыдущий совет по использованию), в дополнительной таблице Выходная таблица результатов (Output Results Table) будут отсутствовать данные для поля SA (Пространственная автокорреляция). Поскольку файлы DBF (.dbf) не сохраняют нулевые значения, они могут быть выражены очень-очень маленькими (отрицательными) числами (где-то -1.797693e+308). Для таблиц базы геоданных эти отсутствующие значения отображаются как нулевые. Отсутствующее значение указывает, что невязки для связанной модели не были проверены на пространственную автокорреляцию, так как эта модель не соответствует всем другим критериям поиска модели.
Файл матрицы пространственных весов по умолчанию, используемый для запуска инструмента Пространственная автокорреляция (Глобальный индекс Морана I) , основан на концептуализации пространственных взаимоотношений 8 ближайших соседей. Значение по умолчанию было выбрано из-за быстрого времени выполнения. Чтобы определить соседские отношения по-разному, можно просто создать собственный файл матрицы пространственных весов с помощью инструмента Построить файл матрицы пространственных весов , затем указать имя этого файла в параметре Выходной файл матрицы пространственных весов (Input Spatial Weights Matrix File). Значения Обратные расстояния (Inverse Distance), Близость полигонов (Polygon Contiguity), К ближайших соседей (K Nearest Neighbors) можно использовать для параметра Определение пространственных взаимоотношений (Conceptualization of Spatial Relationships) для тестирования отклонений регрессии.
Синтаксис
ExploratoryRegression_stats (Input_Features, Dependent_Variable, Candidate_Explanatory_Variables, {Weights_Matrix_File}, {Output_Report_File}, {Output_Results_Table}, {Maximum_Number_of_Explanatory_Variables}, {Minimum_Number_of_Explanatory_Variables}, {Minimum_Acceptable_Adj_R_Squared}, {Maximum_Coefficient_p_value_Cutoff}, {Maximum_VIF_Value_Cutoff}, {Minimum_Acceptable_Jarque_Bera_p_value}, {Minimum_Acceptable_Spatial_Autocorrelation_p_value})| Параметр | Объяснение | Тип данных |
Input_Features | Класс или слой объектов, содержащий зависимую переменную и потенциальные независимые переменные для анализа. | Feature Layer |
Dependent_Variable | Числовое поле, содержащее наблюдаемые значения, которые нужно смоделировать с помощью OLS. | Field |
Candidate_Explanatory_Variables [Candidate_Explanatory_Variables,...] | Перечень полей, используемых в качестве независимых переменных в модели OLS. | Field |
Weights_Matrix_File (Дополнительный) | Файл, содержащий пространственные веса, которые определяют пространственные отношения между входными объектами. Этот файл используется для оценки пространственной автокорреляции среди невязок регрессии. Его можно создать с помощью инструмента Построить файл матрицы пространственных весов. Если файл матрицы пространственных весов не указан, пространственная автокорреляция невязок оцениваются на основании 8 ближайших соседей каждого объекта. Примечание. Файл матрицы пространственных весов используется только для анализа пространственной структуры в невязках модели. Он не применяется для построения или калибровки моделей OLS. | File |
Output_Report_File (Дополнительный) | Файл отчета содержит результаты, в том числе сведения о всех моделях, которые соответствуют введенным критериям. Этот выходной файл также содержит данные диагностики для исправления распространенных проблем регрессии, если вам не удастся найти подходящие модели. | File |
Output_Results_Table (Дополнительный) | Дополнительная выходная таблица, содержит независимые переменные и данные диагностики для всех моделей с указанными p-значениями коэффициентов и значениями ФУД (VIF). | Table |
Maximum_Number_of_Explanatory_Variables (Дополнительный) | Оцениваются все модели с независимыми переменными, не превышающими введенные здесь значения. Если, например, параметр Minimum_Number_of_Explanatory_Variables равен 2, а параметр Maximum_Number_of_Explanatory_Variables равен 3, то инструмент Исследовательская регрессия будет пробовать все модели с каждой из возможных комбинаций из трех независимых переменных. | Long |
Minimum_Number_of_Explanatory_Variables (Дополнительный) | Это значение представляет минимальное число независимых переменных для оцениваемых моделей. Если, например, параметр Minimum_Number_of_Explanatory_Variables равен 2, а параметр Maximum_Number_of_Explanatory_Variables равен 3, то инструмент Исследовательская регрессия будет пробовать все модели с каждой из возможных комбинаций из трех независимых переменных. | Long |
Minimum_Acceptable_Adj_R_Squared (Дополнительный) | Это наименьшее значение скорректированного коэффициента детерминации (Adjusted R-Squared), с которым модель проходит проверку. Если модель соответствует всем другим критериям поиска, но имеет значение Adjusted R-Squared меньше введенного здесь значения, то она не будет показана как проходящая модель в выходном файле отчета Output_Report_File. Корректные значения параметров лежат в диапазоне от 0,0 до 1,0. Значение по умолчанию равно 0.5, что указывает на то, что проходящие модели будут объяснять как минимум 50 процентов изменения в зависимой переменной. | Double |
Maximum_Coefficient_p_value_Cutoff (Дополнительный) | Для каждой оцениваемой модели OLS вычисляет p-значения коэффициентов независимой переменной. Пороговое p-значение, вводимое здесь, представляет уровень уверенности, необходимый для всех коэффициентов в модели, чтобы считать модель проходящей. Небольшие p-значения отражают высокий уровень уверенности. Корректные значения для этого параметра лежат в диапазоне от 1,0 до 0,0, но чаще всего это значения 0,1, 0,05, 0,01, 0,001 и т. д. Значение по умолчанию равно 0.05, что указывает на то, что проходящие модели будут содержать только независимые переменные, коэффициенты которых статистически находятся на уровне доверия 95 % (p-значения меньше 0,05). Чтобы ослабить это значение по умолчанию введите большее пороговое p-значение, например 0.1. Если вы получаете множество проходящих моделей, сделайте этот критерий поиска более строгим, уменьшив пороговое p-значение с 0.05 до 0.01 или меньше. | Double |
Maximum_VIF_Value_Cutoff (Дополнительный) | Это значение отражает допустимую избыточность (мультиколлинеарность) независимых переменных модели. Если значение VIF (фактор увеличения дисперсии) превышает 7,5, мультиколлинеарность может сделать модель нестабильной; следовательно, в данном случае значение 7.5 является значением по умолчанию. Если вы хотите, чтобы ваши проходящие модели были менее избыточными, введите для этого параметра меньшее значение, например – 5.0. | Double |
Minimum_Acceptable_Jarque_Bera_p_value (Дополнительный) | p-значение, возвращаемое диагностическим тестом Жака-Бера определяет, имеют ли невязки модели нормальное распределение. Если p-значение статистически значимое (небольшое), невязки модели не являются нормальными, а модель смещена. У проходящих моделей должны быть большие p-значения Жака-Бера. Минимально допустимое p-значение равно 0,1. Только модели с p-значениями больше этого минимума считаются проходящими. Если у вас не получается найти несмещенные проходящие модели и вы решили ослабить этот критерий, введите меньшее минимальное p-значение, например – 0.05. | Double |
Minimum_Acceptable_Spatial_Autocorrelation_p_value (Дополнительный) | Для моделей, которые соответствуют всем другим критериям, инструмент Исследовательская регрессия проверяет невязки модели на пространственную кластеризацию с помощью Глобального индекса Морана I. Если p-значение для этого диагностического теста статистически значимо (небольшое), в модели, скорее всего, недостаточно важных независимых переменных (она описывает не все явление). К сожалению, имеется пространственная автокорреляция невязок, модель задана неправильно и вы не можете доверять результатам. У проходящих моделей должны быть большие p-значения для этого теста. Минимальное p-значение по умолчанию равно 0.1. Только модели с p-значениями больше этого минимума считаются проходящими. Если у вас не получается найти должным образом заданные модели из-за этого диагностического теста и вы решили смягчить этот критерий, введите меньшее минимальное p-значение, например – 0.05. | Double |
Пример кода
ExploratoryRegression. Пример 1 (окно Python)
Следующий скрипт в окне Python демонстрирует, как использовать инструмент ExploratoryRegression.
import arcpy
import os
arcpy.env.workspace = r"C:\ER"
arcpy.ExploratoryRegression_stats("911CallsER.shp",
"Calls",
"Pop;Jobs;LowEduc;Dst2UrbCen;Renters;Unemployed;Businesses;NotInLF; \
ForgnBorn;AlcoholX;PopDensity;MedIncome;CollGrads;PerCollGrd; \
PopFY;JobsFY;LowEducFY",
"BG_911Calls.swm", "BG_911Calls.txt", "",
"MAX_NUMBER_ONLY", "5", "1", "0.5", "0.05", "7.5", "0.1", "0.1")
ExploratoryRegression. Пример 2 (автономный скрипт Python)
Следующий автономный скрипт Python демонстрирует, как использовать инструмент ExploratoryRegression.
# Exploratory Regression of 911 calls in a metropolitan area
# using the Exploratory Regression Tool
# Import system modules
import arcpy
import os
# Set property to overwrite existing output, by default
arcpy.env.overwriteOutput = True
try:
# Set the current workspace (to avoid having to specify the full path to
# the feature classes each time)
arcpy.env.workspace = r"C:\ER"
# Join the 911 Call Point feature class to the Block Group Polygon feature class
# Process: Spatial Join
fieldMappings = arcpy.FieldMappings()
fieldMappings.addTable("BlockGroups.shp")
fieldMappings.addTable("911Calls.shp")
sj = arcpy.SpatialJoin_analysis("BlockGroups.shp", "911Calls.shp", "BG_911Calls.shp",
"JOIN_ONE_TO_ONE",
"KEEP_ALL",
fieldMappings,
"COMPLETELY_CONTAINS", "", "")
# Delete extra fieldsto clean up the data
# Process: Delete Field
arcpy.DeleteField_management("BG_911Calls.shp", "OBJECTID;INC_NO;DATE_;MONTH_;STIME; \
SD_T;DISP_REC;NFPA_TYP;CALL_TYPE;RESP_COD;NFPA_SF; \
SIT_FND;FMZ_Q;FMZ;RD;JURIS;COMPANY;COMP_COD;RESP_YN; \
DISP_DT;DAY_;D1_N2;RESP_DT;ARR_DT;TURNOUT;TRAVEL; \
RESP_INT;ADDRESS_ID;CITY;CO;AV_STATUS;AV_SCORE; \
AV_SIDE;Season;DayNight")
# Create Spatial Weights Matrix for Calculations
# Process: Generate Spatial Weights Matrix
swm = arcpy.GenerateSpatialWeightsMatrix_stats("BG_911Calls.shp", "TARGET_FID", "BG_911Calls.swm",
"CONTIGUITY_EDGES_CORNERS",
"EUCLIDEAN", "1", "", "", "ROW_STANDARDIZATION", "", "", "", "")
# Exploratory Regression Analysis for 911 Calls
# Process: Exploratory Regression
er = arcpy.ExploratoryRegression_stats("BG_911Calls.shp",
"Calls",
"Pop;Jobs;LowEduc;Dst2UrbCen;Renters;Unemployed;Businesses;NotInLF; \
ForgnBorn;AlcoholX;PopDensity;MedIncome;CollGrads;PerCollGrd; \
PopFY;JobsFY;LowEducFY",
"BG_911Calls.swm", "BG_911Calls.txt", "",
"MAX_NUMBER_ONLY", "5", "1", "0.5", "0.05", "7.5", "0.1", "0.1")
except:
# If an error occurred when running the tool, print out the error message.
print(arcpy.GetMessages())
Параметры среды
Информация о лицензиях
- ArcGIS Desktop Basic: Да
- ArcGIS Desktop Standard: Да
- ArcGIS Desktop Advanced: Да
Связанные разделы
- Обзор группы инструментов Моделирование пространственных отношений (Modeling Spatial Relationships)
- Как работает инструмент Исследовательская регрессия (Exploratory Regression)
- Основы регрессионного анализа
- Что вам не говорят о регрессионном анализе
- Интерпретация результатов инструмента Исследовательская регрессия
- Интерпретация результатов ГВР (OLS)
- Географически взвешенная регрессия
- Пространственная автокорреляция (Глобальный индекс Морана I)
- Что такое z-оценка? Что такое p-значение?
- Как работает регрессия OLS (МНК – метод наименьших квадратов)