При запуске инструмента Исследовательская регрессия основным результатом является отчет. Отчет можно просмотреть в окне сообщений геообработки в фоновом режиме либо в окне Результаты. При необходимости также создается таблица, которая может помочь исследовать протестированные модели. Одна из целей отчета – показать, дают ли потенциальные независимые переменные правильные модели OLS. Если не удалось получить проходящие модели (модели, соответствующие всем указанным критериям после запуска инструмента Исследовательская регрессия, в отчете также будет показано, какие переменные являются согласованными предикторами, что позволяет определить, в каких диагностических тестах возникла ошибка. Стратегии по устранению проблем, связанных с каждым диагностическим тестом, указаны в документе Основы регрессионного анализа (см. раздел Типичные проблемы с регрессией, последствия и решения) и в разделе Что вам не говорят о регрессионном анализе. Дополнительные сведения о том, как узнать, является ли модель OLS правильной, см. в разделах Основы регрессионного анализа и Интерпретация результатов МНК (метода наименьших квадратов).
Отчет
В отчете инструмента Исследовательская регрессия пять разделов. Каждый из них описывается ниже.
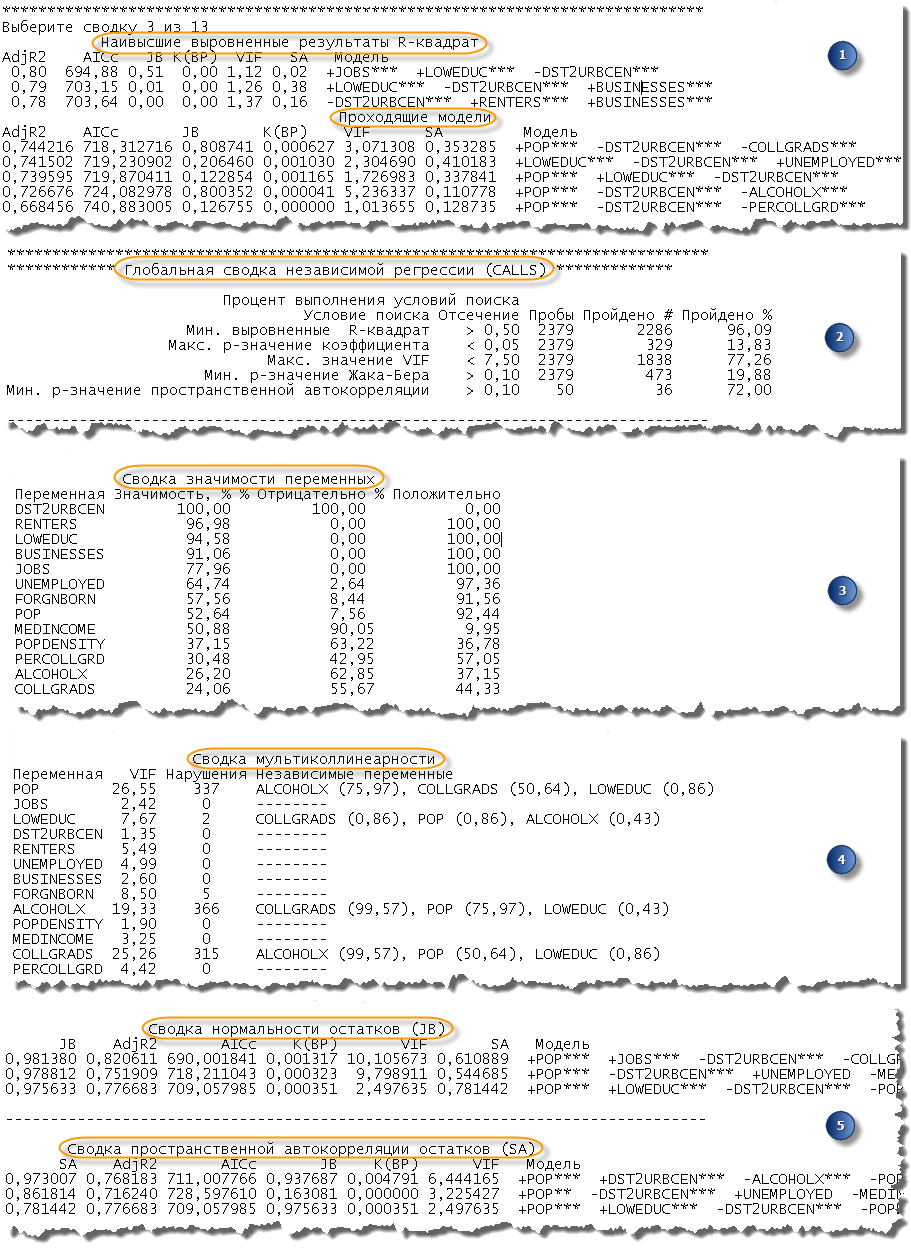
1. Лучшие модели по числу независимых переменных
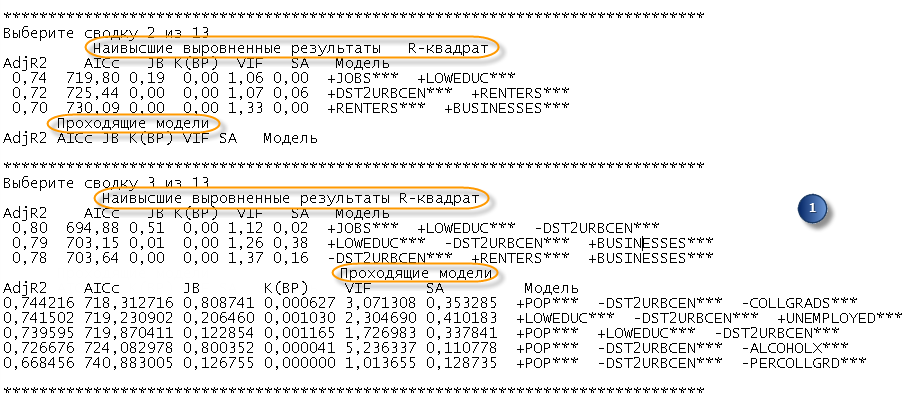
Первый набор сводных данных в отчете группируется по числу независимых переменных в проверенных моделях. Если указать число 1 для параметра Минимальное число независимых переменных (Minimum Number of Explanatory Variables) и значение 5 для параметра Максимальное число независимых переменных (Maximum Number of Explanatory Variables), в отчете будет 5 сводных разделов. В каждом из них указывается три модели с наибольшими скорректированными значениями R2, а также все проходящие модели. В каждом разделе также указаны диагностические значения для каждой модели: скорректированный информационный критерий Акаике – AICc, p-значение Жака-Бера – JB, стьюдентизированное Кенкером p-значение Бреуша-Пагана – K(BP), наибольший Фактор увеличения дисперсии – VIF, а также измерение пространственной автокорреляции отклонений (p-значение глобального индекса Морана I) – SA. Эти сводные сведения позволяют понять, как хорошо ваши модели прогнозируют данные (Adj R2) и проходят ли модели все указанные диагностические критерии. Если вы приняли все критерии поиска по умолчанию (параметры Минимальный допустимый скорректированный коэффициент детерминации (Minimum Acceptable Adj R Squared), Максимальный порог p-значения коэффициента (Maximum Coefficient p-value Cutoff), Максимальный порог значения VIF (Maximum VIF Value Cutoff), Минимально допустимое p-значение Жака-Бера (Minimum Acceptable Jarque Bera p-value) и Минимально допустимое p-значение пространственной автокорреляции (Minimum Acceptable Spatial Autocorrelation p-value)), все модели в списке Проходящие модели (Passing Models) будут правильными моделями OLS.
Если проходящих моделей нет, в остальном отчете все равно будет представлена полезная информация о переменных отношений, которая может помочь при принятии решений о дальнейших действиях.
2. Глобальная сводка исследовательской регрессии

Раздел Глобальная сводка исследовательской регрессии – это важное место для начала анализа, особенно если вы не нашли проходящие модели, так как в нем показано, почему модели не прошли проверки. В данном разделе перечислены пять диагностических тестов и процент моделей, прошедших каждый из них. Если проходящих моделей нет, эта информация позволит определить, в каком тесте возникают проблемы.
Часто неприятности возникают с тестом глобального индекса Морана I для пространственной автокорреляции (SA). Если у всех проверенных моделей есть невязки регрессии с пространственной автокорреляцией, чаще всего это указывает на отсутствие важных независимых переменных. Один из лучших способов узнать, отсутствуют ли независимые переменные – изучить карту невязок, созданную инструментом Регрессия методом наименьших квадратов (OLS). Выберите одну из моделей исследовательской регрессии, которая хорошо прошла все другие критерии (используйте списки наибольших значений скорректированных коэффициентов детерминации или выберите модель из дополнительной выходной таблицы) и запустите OLS с использованием этой модели. Выходные данные инструмента Регрессия методом наименьших квадратов (OLS) – это карта невязок модели. Изучите невязки модели, чтобы получить сведения о недостающих данных. Попробуйте сформировать наибольшее число потенциальных пространственных переменных, таких как расстояние до центра города, больниц и других географических объектов. Попробуйте использовать переменные пространственного режима. Например, если все недооценки расположены в сельских областях, создайте бинарную переменную и посмотрите, улучшатся ли результаты регрессионного анализа.
Другой диагностический тест, которые вызывает проблемы – это тест Жака-Бера для невязок с нормальным распределением. Если ни одна из моделей не проходит тест Жака-Бера (JB), налицо проблема со смещением модели. Распространенные причины смещения модели:
- Нелинейные отношения
- Выбросы данных
При просмотре матрицы рассеивания возможных независимых значений по отношению к зависимой переменной, вы увидите, имеет ли место одна из этих проблем. Дополнительные стратегии описаны в документе Основы регрессионного анализа. Если модели не проходят тест пространственной автокорреляции (SA), исправьте сначала эти проблемы. Смещение может быть вызвано отсутствием важных независимых переменных.
3. Сводка значимости переменных
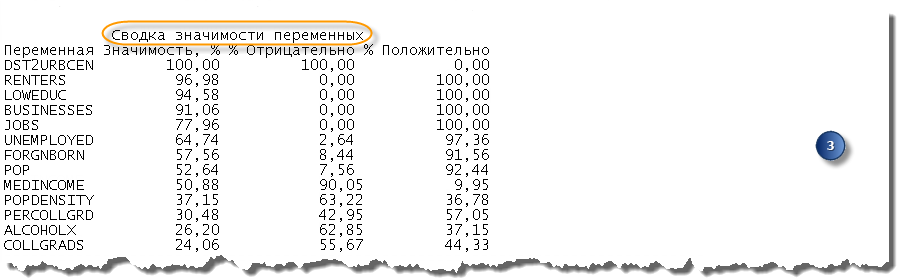
В разделе Сводка значимости переменных (Summary of Variable Significance) представлены сведения об отношениях переменных и их согласованности. В нем указана каждая потенциальная независимая переменная с отношением количества раз, когда она была статистически значимой. У первых нескольких переменных в списке самые большие значения столбца % Significant. Вы также можете увидеть стабильность отношений переменных, изучив столбцы % Negative и % Positive. Сильные предикторы будут постоянно значимы (% Significant), а отношения будут стабильными (в основном отрицательными или в основном положительными).
Эта часть отчета также позволяет повысить эффективность модели. Это особенно важно при работе с множеством возможных независимых значений (больше 50) и использовании моделей с пятью или большим числом предикторов. При наличии большого числа независимых переменных и проверке многих комбинаций, вычисления могут занять длительное время. В некоторых случаях, фактически, инструмент не закончит работу из-за ошибок памяти. Рекомендуется постепенно увеличить число проверяемых моделей: начните с установки для параметров Минимальное число независимых переменных (Minimum Number of Explanatory Variables) и Максимальное число независимых переменных (Maximum Number of Explanatory Variables) значение 2, затем 3, затем 4 и т. д. С каждым запуском удаляются переменные, которые редко являются статистически значимыми для проверяемых моделей. В разделе Сводка значимости переменных (Summary of Variable Significance) вы сможете найти эти переменные, а также сильные предикторы. Удаление даже одной потенциальной независимой переменной из списка может значительно сократить время работы инструмента Исследовательская регрессия.
4. Сводка мультиколлинеарности

Раздел отчета Сводка мультиколлинеарности (Summary of Multicollinearity) можно использовать вместе с разделом Сводка значимости переменных (Summary of Variable Significance) для определения того, какие потенциальные независимые переменные можно удалить из анализа для улучшения производительности. Раздел Сводка мультиколлинеарности (Summary of Multicollinearity) позволяет узнать, сколько раз каждая независимая переменная была включена в модель с высокой степенью мультиколлинеарности, а также узнать другие независимые переменные, также включенные в эти модели. Если две (или более) независимых переменных часто обнаруживаются в моделях с высокой мультиколлинеарностью, эти переменные могут описывать один и тот же аспект явления. Так как требуется включать только переменные, которые описывают уникальный аспект зависимой переменной, можно выбрать только одну из избыточных переменных для дальнейшего анализа. Можно выбрать самую полезную переменную в разделе Сводка значимости переменных (Summary of Variable Significance).
5. Дополнительные сводные данные диагностики

Конечные сводные данные диагностики отображают наибольшие p-значения Жака-Бера (Сводка нормальности остатков (Summary of Residual Normality)) и наибольшие p-значения глобального индекса Морана I (Сводка пространственной автокорреляции остатков (Summary of Residual Autocorrelation)). Чтобы пройти эти диагностические тесты, необходимы большие p-значения.
Эти сводные данные не слишком полезны, если модели проходят тест Жака-Бера и тест пространственной автокорреляции (глобальный индекс Морана I), так как если критерий статистической значимости равен 0,1, все модели со значениями более 0,1 также будут проходящими. Но эти сводные данные полезны, если у вас нет проходящих моделей, и вы хотите узнать, насколько вы далеки от нормально распределенных невязок или невязок без статистически значимой пространственной автокорреляции. Например, если p-значения для сводки Жака-Бера равны 0,000000, ясно, что вы очень далеки от нормально распределенных невязок. Или же, если p-значения равны 0,092, то вы близки к нормально распределенным невязкам (к слову, в зависимости от выбранного уровня значимости p-значение 0,092 может быть достаточным). Эти сводные данные демонстрируют, насколько серьезна проблема, и, если ни одна из моделей не является проходящей, какие переменные, связанные с моделями, хотя бы близки к прохождению тестов.
Таблица
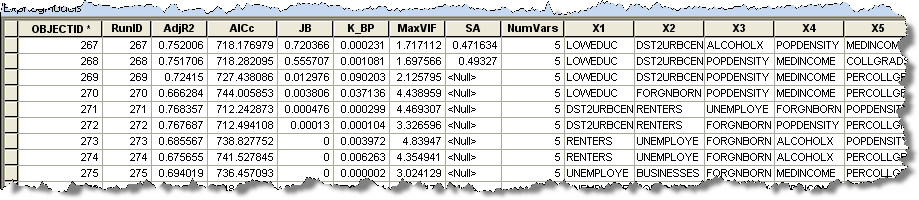
Если указано значение для параметра Выходная таблица результатов (Output Results Table), будет создана таблица со всеми моделями, соответствующими критериям Максимальный порог p-значения коэффициента (Maximum Coefficient p-value Cutoff) и Максимальный порог значения VIF (Maximum VIF Value Cutoff). Даже если проходящих моделей нет, существует вероятность того, что в выходной таблице будут какие-то модели. Каждая строка в таблице представляет модель, соответствующую критериям коэффициентов и значений VIF. Столбцы в таблице описывают диагностические тесты и независимые переменные модели. Диагностические данные: скорректированный коэффициент детерминации (R2), скорректированный информационный критерий Акаике – AICc, p-значение Жака-Бера – JB, стьюдентизированное Кенкером p-значение Бреуша-Пагана – K(BP), наибольший Фактор увеличения дисперсии – VIF, а также p-значение глобального индекса Морана I – SA. Вы можете отсортировать модели по их значениям AICc. Чем меньше значение AICc, тем лучше работает модель. Вы можете отсортировать значения AICc в ArcMap, дважды щелкнув столбец AICc. Если вы выбираете модель для применения в анализе OLS (для изучения невязок), то помните о том, что нужно выбрать модель с малым значением AICc и проходящими значениями для максимального числа других диагностических данных. Например, если вы изучили выходной отчет и поняли, что тест Жака-Бера вызвал проблемы, ищите модель с наименьшим значением AICc, которая соответствует всем критериям, кроме Жака-Бера.
Дополнительные ресурсы
Если у вас нет опыта регрессионного анализа в ArcGIS, настоятельно рекомендуем просмотреть бесплатный семинар по регрессии Esri Virtual Campus, а затем запустить Руководство по регрессионному анализу перед использованием инструмента Исследовательская регрессия.
Возможно, вы также захотите просмотреть следующие разделы:
- Более подробно о работе инструмента Исследовательская регрессия
- Что вам не говорят о регрессионном анализе
- Основы регрессионного анализа
Burnham, K.P. and D.R. Anderson. 2002. Model Selection and Multimodel Inference: a practical information-theoretic approach, 2nd Edition. New York: Springer. Section 1.5.
Кроме того, на странице ресурсов по пространственной статистике можно найти новые видео, учебные пособия и другие материалы.