Функции преобразования доступны для Изменения масштаба по функции.

Доступно с лицензией Spatial Analyst.

Инструмент Пересчёт по функции (Rescale by Function) перемасштабирует значения входного растра на основе заданной функции преобразования. Существуют различные функции преобразования и каждая из них изменяется при вычислении и применении. Какую из функций следует использовать, зависит от того, какая из функций лучше всего отражает изучаемое явление. Далее вы можете повторно определить характеристики каждой функции через ряд входных параметров.

Для того чтобы получить максимум полезной информации в этом разделе, советуем вам ознакомиться с основными терминами, используемыми для данного инструмента. Чтобы лучше понять, как нижний и верхний пороги функции преобразования влияют на выходные значения, см. Взаимодействие нижнего и верхнего порогов для выходных значений (The interaction of the lower and upper thresholds on the output values).

Перечень функций

В следующей таблице приводится краткая информация о каждой функции, со ссылками, которые приведут вас к предметному обсуждению данной функции.

Экспоненциальный	Используется, когда предпочтение увеличивается с увеличением входных значений и предпочтение растет тем быстрее, чем больше становятся входные значения.
Гауссово	Используется, когда наивысшее предпочтение отдаётся определенному входному значению, с предпочтениями, уменьшающимися по мере удаления входных значений от данного значения.
Большой	Используется для указания того, что большие входные значения имеют более высокое предпочтение.
Линейная	Изменяет масштаб входных значений с использованием линейной функции.
Логарифм	Используется, когда предпочтение для низких входных значений быстро увеличивается с увеличением входных значений и, затем, предпочтение сужается с дальнейшим увеличением входных значений.
Logistic Decay	Используется, когда малые входные значения являются более предпочтительными. По мере увеличения входных значений, предпочтения быстро возрастают, пока не будут сужены при больших входных значениях.
Logistic Growth	Используется, когда большие входные значения являются более предпочтительными. По мере увеличения значений, предпочтения быстро увеличиваются, пока не будут сужены при больших входных значениях.
MSLarge	Изменяет масштаб входных данных на основе среднего и стандартного отклонения, где большие значения во входном растре имеют более высокое предпочтение.
MSSmall	Изменяет масштаб входных данных на основе среднего и стандартного отклонения, где меньшие значения во входном растре имеют более высокое предпочтение.
Ближайший	Используется, когда более предпочтительны значения очень близкие к середине.
Степень	Используется, когда предпочтение для входных значений быстро увеличивается с увеличением входных значений.
Небольшие	Используется для указания того, что меньшие значения входного растра имеют более высокое предпочтение.
Симметричный линейный	Используется, когда определенное входное значение является наиболее предпочтительным, с предпочтениями, линейно уменьшающимися по мере удаления входных значений от точки.

Обзоры и иллюстрации функций

Для каждой функции будут представлены: общий обзор, вариант использования и подробную информацию о воздействии некоторых входных параметров на кривую функции.

Обзор

В Обзоре описаны основные свойства, а также конкретные поведения для каждой функции.

Случай применения

Вариант использования описывает конкретный, реальный пример, для которого хорошо подходит конкретная функция.

Влияние параметров

В этом разделе мы обсудим, как форморегулирующие параметры влияют на функцию. Будет описано, как изменение значения параметра будет влиять на кривую, и показан график при нескольких различных значениях параметра для иллюстрации этого влияния. Также будет включено выражение класса Python, демонстрирующее, как построена функция преобразования, показанная на графиках.

Примечание:

Для каждого примера графика, входными данными является растр, значения которого варьируются в диапазоне от 0 до 500. Для этого конкретного выбора нет особой причины, но он используется последовательно для всех графиков с тем, чтобы сделать легче их сравнение. На практике, реальные входные растры могут иметь любой диапазон входных значений.

Экспоненциальная функция

Обзор

Экспоненциальная функция преобразует входные данные посредством применения экспоненциальной функции с использованием сдвига и базового коэффициента. В модели пригодности, эту функцию лучше использовать, когда предпочтение для местоположений с низкими входными значениями наименьшее, но предпочтения быстро увеличиваются для местоположений ячеек с большими значениями.

Случай применения

Рассмотрим порядок изменения масштаба расстояния от источников воды для модели пригодности мест обитания черепахи. Черепахи предпочитают жить в местах, расположенных ближе к воде, из-за их ограниченной подвижности. Предпочтение для местоположений, расположенных дальше от воды, быстро уменьшается по мере увеличения расстояния.

Влияние параметров

Входной сдвиг

Сдвиг входных данных (Input shift) – значение, вычитаемое из входного значений. Экспоненциальная функция применяется к сдвинутым входным значениям для определения значений функции.

Базовый коэффициент

Параметр Базовый коэффициент (Base factor) контролирует, как круто возрастает экспоненциальная функция. По мере увеличения базового коэффициента, предпочтение для низких входных значений медленно увеличивается с увеличением входных значений и, затем, предпочтение быстро возрастает при более высоких входных значениях. Изменение этого параметра может быть полезно, если диапазон входных данных мал (например, от 0 до 1), и вы хотите сохранить экспоненциальную кривую между минимальным и максимальным значениями.

Примерные графики Экспоненциальной функции, показывающие влияние изменения значения Базового коэффициента.

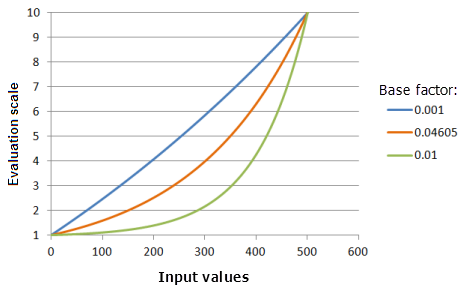
Функция, использованная для графика выше:

• TfExponential(0.002651, BaseFactor, 0, 1, 500, 10)

  Где значения, использованные для BaseFactor, включают: 0,001. 0,04605 и 0,01. Сдвиг (Shift), равный 0,002651, и Базовый коэффициент (Base factor), равный 0,04605, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Гауссова функция

Обзор

Гауссова (Gaussian) функция преобразует входные значения с использованием нормального распределения. При применении увеличивающейся оценочной шкалы, середина нормального распределения определяет наиболее предпочтительное значение. Если середина расположена между нижним и верхним порогами, входное значение, равное середине, присваивается значению До масштаба (To scale). Остальные входные значения снижаются по оценочной шкале (снижение предпочтения), так как их значения удаляются от середины в обоих направлениях, пока они не достигнут значения От масштаба (From scale). В модели пригодности, эта функция особенно полезна, если наибольшее предпочтение отдаётся близкому к известному значению, с предпочтениями, уменьшающимися по мере удаления входных значений от данного значения.

Случай применения

При установке солнечных панелей, выбор правильного направления для расположения рабочей поверхности важен для обеспечения максимальной выдачи энергии. Для северного полушария наиболее предпочтительны южные склоны (180 градусов). Предпочтение для склонов обращённых все больше и больше на восток и запад непрерывно уменьшается, пока не будет достигнуто направление на север, которое является наименее предпочтительным.

Влияние параметров

Середина

Параметр Середина (Midpoint) определяет центр Гауссовой кривой. Вы можете сдвинуть середину функции от середины данных в сторону более низких или более высоких значений, которые могут быть важны более или менее. Вторая причина, по которой вы можете захотеть перенести середину состоит в том, чтобы вписать функцию в значения критерия за пределами диапазона данных.

Середина может контролировать диапазон входных значений, охватываемых кривой функции.

Примерные графики Гауссовой функции, показывающие влияние изменения значения Середины.

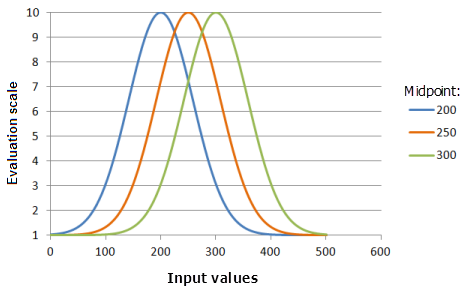
Функция, использованная для графика выше:

• TfGaussian(Midpoint, 0.000147, 0, 1, 500, 10)

  Где значения середины Midpoint) - 200, 250 и 300. Середина (Midpoint), равная 250, и Разброс (Spread), равный 0,0000147, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Разброс

Параметр Разброс (Spread) регулирует крутизну распада от середины. Чем больше значение, тем уже становится кривая вокруг середины (предпочтение снижается более быстро).

Примерные графики Гауссовой функции, показывающие влияние изменения значения Разброса

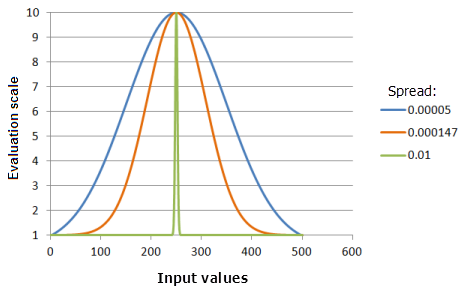
Функция, использованная для графика выше:

• TfGaussian(250, Spread, 0, 1, 500, 10)

  Где значения, использованные для Spread, включают: 0,00005, 0,000147 и 0,01. Середина (Midpoint), равная 250, и Разброс (Spread), равный 0,0000147, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Функция Большой (Large)

Обзор

Функция преобразования Большой (Large) используется, если большие входные значения являются более предпочтительными. Заданная середина определяет точку перехода для функции. Значения выше середины, увеличиваются в предпочтении и значения ниже середины уменьшаются в предпочтении. Как быстро значения будут увеличиваться и уменьшаться по мере удаления от середины, определяется форморегулирующим параметром Разброс (Spread).

Случай применения

Для создания модели пригодности товаров для торговли, вы можете перемасштабировать критерий доходности кофе. Местоположения с более высокой доходностью, являются более предпочтительными, с предпочтениями, увеличивающимися нелинейно с ростом доходности.

Влияние параметров

Середина

Параметр Середина (Midpoint) определяет точку перехода функции. Сдвиг её в сторону меньших, чем середина, значений во входных данных изменяет точку перехода, что приводит к увеличению в диапазоне больших значений, которые являются более предпочтительными справа от середины, с предпочтением, увеличивающимся быстрее.

Примерные графики функции Большой (Large), показывающие влияние изменения значения Середины.

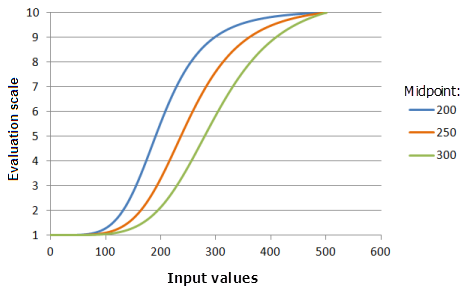
Функция, использованная для графика выше:

• TfLarge(Midpoint, 5, 0, 1, 500, 10)

  Где значения середины Midpoint - 200, 250 и 300. Середина (Midpoint), равная 250, и Разброс (Spread), равный 5, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Разброс

Параметр Разброс (Spread) контролирует, как быстро возрастает и убывает предпочтение. По мере увеличения разброса, входные значения, превышающие середину, будут быстрее увеличиваться в предпочтении при приближении к верхнему порогу, и входные значения, меньшие, чем середина, будут быстрее снижаться в предпочтении при приближении к нижнему порогу.

Примерные графики функции Большой (Large), показывающие влияние изменения значения Разброса

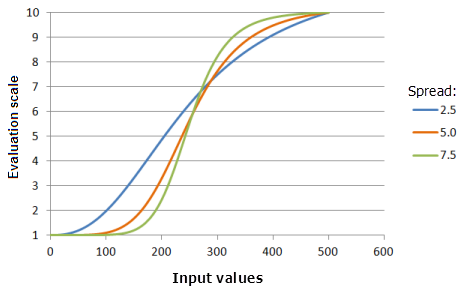
Функция, использованная для графика выше:

• TfLarge(250, Spread, 0, 1, 500, 10)

  Где значения середины Spread - 2,5, 5,0 и 7,5. Разброс (Spread), равный 5, и Середина (Midpoint), равная 250, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Линейная функция

Обзор

Функция Линейного (Linear) преобразования применяет линейную функцию между заданными минимальным и максимальным значениями. Если От масштаба (From scale) больше, чем До масштаба (To scale), то устанавливается отрицательная (негативная) линейная зависимость (отрицательный наклон).

Эта функцию лучше использовать, когда предпочтения для значений увеличиваются или уменьшаются с постоянной линейной скоростью.

Случай применения

Чтобы создать модели пригодности изменений климата для обитания диких животных, вам может понадобиться изменить масштаб предпочтения обитания диких животных для значений высот. В исследуемом районе, большие значения высоты являются более предпочтительными.

Влияние параметров

Минимум (Minimum)

Параметр Минимум (Minimum) устанавливает первую точку, через которую должна пройти Линейная функция. Вы можете изменить значение параметра от минимума входных данных для соответствия предпочтения явления критерию.

Примерные графики функции Линейная (Linear), показывающие влияние изменения значения Минимума.

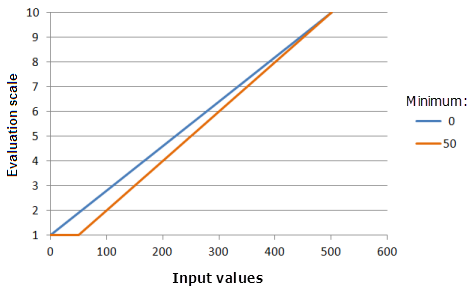
Функция, использованная для графика выше:

• TfLinear(Minimum, 500, 0, 1, 500, 10)

  Где значения минимума Minimum - 0 и 50. Минимум (Minimum), равный 0, и Максимум (Maximum), равный 500, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Максимум (Maximum)

Параметр Максимум (Maximum) устанавливает вторую точку, через которую должна пройти Линейная функция. Вы можете изменить значение параметра от максимума входных данных для соответствия предпочтения явления критерию.

Примерные графики функции Линейная (Linear), показывающие влияние изменения значения Максимума.

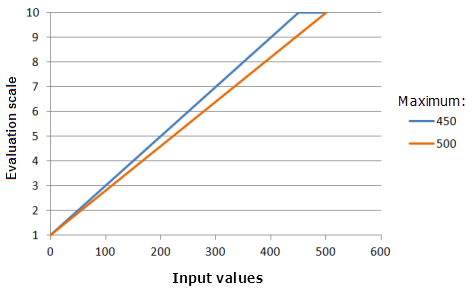
Функция, использованная для графика выше:

• TfLinear(0, Maximum, 0, 1, 500, 10)

  Где значения максимума Maximum - 450 и 500. Минимум (Minimum), равный 0, и Максимум (Maximum), равный 500, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Логарифмическая функция

Обзор

Логарифмическая функция преобразования применяет логарифмическую функцию ко входным данным с использованием заданного сдвига и коэффициента. В модели пригодности Логарифмическую функцию лучше всего использовать, когда предпочтения увеличиваются или уменьшаются быстро, а затем сужаются с увеличением входных значений критерия.

Случай применения

Чтобы создать модель пригодности для обитания птиц, вы можете перемасштабировать критерий количества пищи. Предпочтение для мест с низким количеством пищи является наименьшим, если оно не может поддерживать жизнедеятельность птиц. Когда есть достаточно пищи для выживания, предпочтение быстро растет в местах с более высоким количеством пищи, так как они наилучшим образом подходят для птиц. В определенной точке, у птиц будет достаточно пищи, поэтому места с еще большим количеством пищи, будут более желательными, но гораздо более медленными темпами.

Влияние параметров

Сдвиг

Сдвиг (Shift) является значением, вычитаемым из входных значений, которое может управлять начальным входным значением для логарифмических вычислений. Например, в случае с птицами, если птицы не могут жить в местах с менее чем 250 единицами пищи, вы можете сдвинуть начальную точку для функции на 250.

Примерные графики Логарифмической функции, показывающие влияние изменения значения Сдвига.

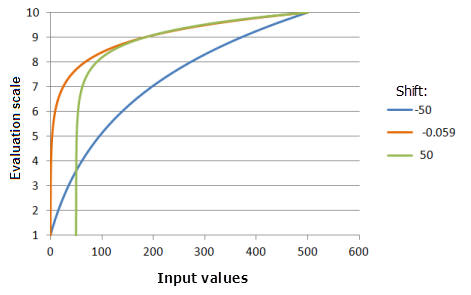
Функция, использованная для графика выше:

• TfLogarithm(Shift, 0.0046, 0, 1, 500, 10)

  Где значения, использованные для Shift, включают: -50,0, -0,059 и 50,0. Сдвиг (Shift), равный -0,059, и Экспонента (Exponent), равная 0,0046, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Показатель

Коэффициент (Factor) представляет собой множитель, который контролирует подъём логарифмической функции. Можно изменить этот параметр, если диапазон входных значений мал (например, от 0 до 1), для поддержки логарифмической кривой между минимальным и максимальным значениями.

Функция Логистического распада (Logistic Decay)

Обзор

Функция преобразования Логистического распада (Logistic Decay) вписывает функцию логистического распада (logistic decay) между заданными минимумом и максимумом с использованием определённого процента отрезка по y. В модели пригодности, функцию логистического распада лучше использовать, когда более низкие входные значения являются более предпочтительными. По мере увеличения входных значений, предпочтения быстро возрастают до точки, где наиболее низкие предпочтения выравниваются при более высоких входных значениях.

Случай применения

Чтобы создать модель пригодности жилья, вы можете перемасштабировать расстояние от электрических линий по стоимости для критерия электроэнергии. Местоположения рядом с существующими электрическими линиями являются более предпочтительными, потому как в них стоимость получения электроэнергии будет меньше. После достижения некоторого расстояния, предпочтения быстро уменьшаются, так как возникнет необходимость установки дополнительных трансформаторов, что влечет дополнительные затраты на оборудование и выполнение работ. Снижение уровней предпочтения выравнивается для удалённых ячеек, так как дополнительные затраты уже не оказывают большого дополнительного влияния на предпочтения, поскольку местоположения уже и так дороги.

Влияние параметров

Минимум (Minimum)

Параметр Минимум (Minimum) контролирует начальную точку логистического распада. Чем больше значение минимума, тем быстрее будут снижаться предпочтения в основной части убывания функции (кривая будет круче).

Примерные графики функции Логистического распада (Logistic Decay), показывающие влияние изменения значения Минимума.

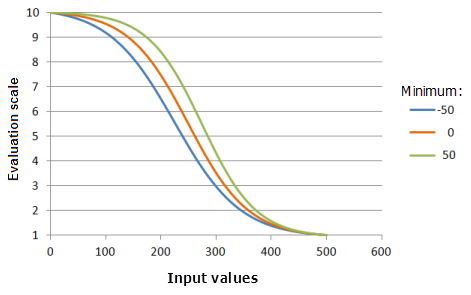
Функция, использованная для графика выше:

• TfLogisticDecay(Minimum, 500, 99, 0, 1, 500, 10)

  Где значения минимума Minimum - -50, 0 и 50. Минимум (Minimum), равный 0, Максимум (Maximum), равный 500, и yInterceptPercent (Процент отрезка по Y), равный 99, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Максимум (Maximum)

Параметр Максимум (Maximum) контролирует конечную точку логистического распада. Чем меньше значение максимума, тем быстрее будут снижаться предпочтения в основной части убывания функции (кривая будет круче).

Примерные графики функции Логистического распада (Logistic Decay), показывающие влияние изменения значения Максимума.

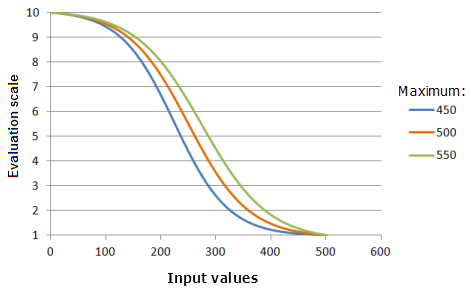
Функция, использованная для графика выше:

• TfLogisticDecay(0, Maximum, 99, 0, 1, 500, 10)

  Где значения, использованные для Maximum, включают: 450, 500 и 550. Минимум (Minimum), равный 0, Максимум (Maximum), равный 500, и yInterceptPercent (Процент отрезка по Y), равный 99, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Процент отрезка по Y

Параметр Процент отрезка по Y (Y intercept percent) определяет диапазон значений, который будет находиться в части распада кривой Логистического распада. Концептуально, можно представить функцию логистического распада в форме обратной "S". Существуют два хвоста, соединенных основной частью "S", которая будет упоминаться как часть распада кривой. Чем больше значение этого параметра, тем меньше будет диапазон входных значений, включенный в часть распада кривой ("S" более вертикально), однако, предпочтение для значений будет снижаться более быстрыми темпами, и кривая будет более выраженной.

Примерные графики функции Логистического распада (Logistic Decay), показывающие влияние изменения значения параметра Процент отрезка по Y (Y intercept percent).

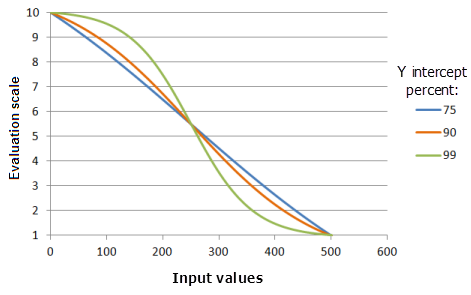
Функция, использованная для графика выше:

• TfLogisticDecay(0, 500, YInterceptPercent, 0, 1, 500, 10)

  Где значения, использованные для Процента отрезка по Y (Y intercept percent), включают: 75, 90 и 99. Минимум (Minimum), равный 0, Максимум (Maximum), равный 500, и yInterceptPercent (Процент отрезка по Y), равный 99, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Функция Логистического роста (Logistic Growth)

Обзор

Функция преобразования Логистический рост (Logistic Growth) сходна с функцией преобразования LogisticDecay, за исключением того, что предпочтения в функции логистического роста возрастают вместо того, чтобы снижаться.

Случай применения

В модели пригодности среды обитания, предпочтения для животного увеличиваются логистически с увеличением доступной пищи. Количество пищи, в первую очередь, должно достичь критического уровня для выживания, затем предпочтение быстро возрастает с увеличением пищи, пока максимальное потребление не будет достигнуто, и в этот момент предпочтения выравниваются.

Влияние параметров

Минимум (Minimum)

Параметр Минимум (Minimum) контролирует начальную точку логистического роста. Чем больше значение минимума, тем быстрее будут увеличиваться предпочтения в основной части роста функции (кривая будет круче).

Примерные графики функции Логистического роста (Logistic Growth), показывающие влияние изменения значения Минимума.

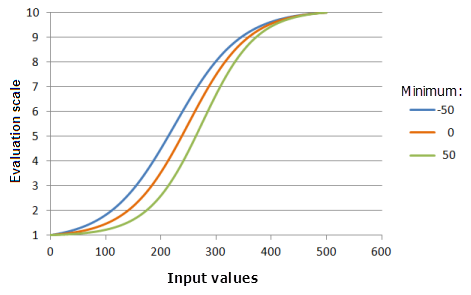
Функция, использованная для графика выше:

• TfLogisticGrowth(Minimum, 500, 1, 0, 1, 500, 10)

  Где значения минимума Minimum - -50, 0 и 50. Минимум (Minimum), равный 0, Максимум (Maximum), равный 500, и yInterceptPercent (Процент отрезка по Y), равный 1, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Максимум (Maximum)

Параметр Максимум (Maximum) контролирует конечную точку логистического роста. Чем меньше значение максимума, тем быстрее будут увеличиваться предпочтения в основной части роста функции (кривая будет круче).

Примерные графики функции Логистического роста (Logistic Growth), показывающие влияние изменения значения Максимума.

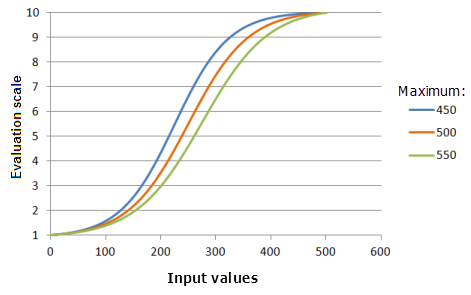
Функция, использованная для графика выше:

• TfLogisticGrowth(0, Maximum, 1, 0, 1, 500, 10)

  Где значения, использованные для Maximum, включают: 450, 500 и 550. Минимум (Minimum), равный 0, Максимум (Maximum), равный 500, и yInterceptPercent (Процент отрезка по Y), равный 1, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Процент отрезка по Y

Параметр Процент отрезка по Y (Y intercept percent) определяет диапазон значений, который будет находиться в части роста кривой Логистического роста. Концептуально, можно представить функцию логистического роста в форме "S". Существуют два хвоста, соединенных основной частью "S", которая будет упоминаться как часть роста кривой. Чем меньше значение параметра yInterceptPercent, тем меньше будет диапазон входных значений, включенный в часть роста кривой ("S" более вертикально), однако, предпочтение для значений будет увеличиваться более быстрыми темпами, и кривая будет более выраженной.

Примерные графики функции Логистического роста (Logistic Growth), показывающие влияние изменения значения параметра Процент отрезка по Y (Y intercept percent).

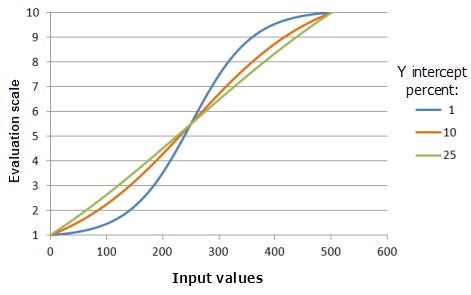
Функция, использованная для графика выше:

• TfLogisticGrowth(0, 500, YInterceptPercent, 0, 1, 500, 10)

  Где значения, использованные для Процента отрезка по Y (Y intercept percent), включают: 1, 10 и 25. Минимум (Minimum), равный 0, Максимум (Maximum), равный 500, и yInterceptPercent (Процент отрезка по Y), равный 1, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Функция MSLarge

Обзор

Функция преобразования MSLarge сходна с функцией преобразования Большой (Large), за исключением того, что определение функции основано на заданном среднем значении и множителях стандартного отклонения. Как правило, разница между этими двумя функциями состоит в том, что функция MSLarge может быть более применима, если очень большие значения являются более предпочтительными.

При определенном сочетании среднего и множителей стандартного отклонения, результат данной функции может быть похож на результат функции Большой (Large).

Случай применения

Как и в модели пригодности предметов потребления для торговли, о которой шла речь в случае использования функции преобразования Большой (Large), исключение мест с более высокой доходностью кофе гораздо предпочтительней в этом случае.

Влияние параметров

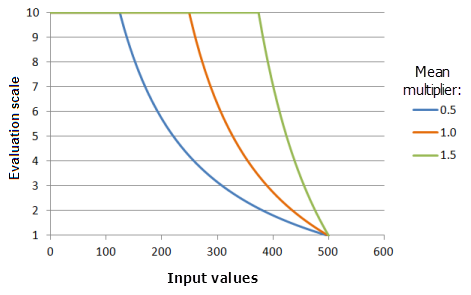
Средний множитель

Параметр Средний множитель (Mean multiplier) контролирует наклон кривой функции. По мере уменьшения множителя, благоприятный диапазон больших значений увеличивается, и, с большими значениями, кривая функции возрастает медленнее при приближении к верхнему порогу.

Примерные графики функции MSLarge, показывающие влияние изменения значения Среднего множителя.

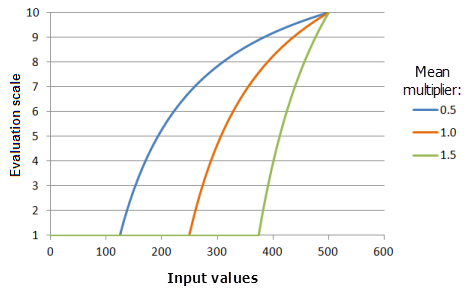
Функция, использованная для графика выше:

• TfMSLarge(MeanMultiplier, 1, 0, 1, 500, 10)

  Где значения, использованные для среднего, включают: 0,5, 1,0 и 1,5. Средний множитель (Mean multiplier), равный 1, и Множитель стандартного отклонения (Standard deviation multiplier), равный 1, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Множитель ср.кв. отклонения

Параметр Множитель стандартного отклонения (Standard deviation multiplier) контролирует наклон кривой функции. По мере увеличения множителя, кривая функции возрастает медленнее.

Примерные графики функции MSLarge, показывающие влияние изменения значения Множителя стандартного отклонения.

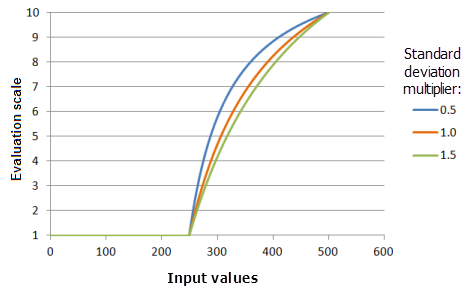
Функция, использованная для графика выше:

• TfMSLarge(1, StandardDeviationMultiplier, 0, 1, 500, 10)

  Где значения, использованные для стандартного отклонения, включают: 0.5, 1.0 и 1.5. Средний множитель (Mean multiplier), равный 1, и Множитель стандартного отклонения (Standard deviation multiplier), равный 1, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Функция MSSmall

Обзор

Функция преобразования MSSmall сходна с функцией преобразования Малый (Small), за исключением того, что определение функции основано на заданном среднем значении и множителях стандартного отклонения. Как правило, разница между этими двумя функциями состоит в том, что функция MSSmall может быть более применима, если очень малые значения являются более предпочтительными.

При определенном сочетании среднего и множителей стандартного отклонения, результат данной функции может быть похож на результат функции Малый (Small).

Случай применения

Подобно перемасштабированию расстояния от дорог по стоимости для критерия строительства в модели пригодности жилья, о которой шла речь в случае использования функции преобразования Малый (Small), исключение ближних местоположений ячеек гораздо предпочтительней в этом случае.

Влияние параметров

Средний множитель

Средний множитель (Mean multiplier): контролирует наклон кривой функции. По мере увеличения множителя, благоприятный диапазон малых значений увеличивается, и, с большими значениями, кривая функции убывает быстрее при приближении к верхнему порогу.

Примерные графики функции MSSmall, показывающие влияние изменения значения Среднего множителя.

Функция, использованная для графика выше:

• TfMSSmall(MeanMultiplier, 1, 0, 1, 500, 10)

  Где значения, использованные для среднего, включают: 0,5, 1,0 и 1,5. Средний множитель (Mean multiplier), равный 1, и Множитель стандартного отклонения (Standard deviation multiplier), равный 1, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Множитель ср.кв. отклонения

Параметр Множитель стандартного отклонения (Standard deviation multiplier) контролирует наклон кривой функции. По мере увеличения множителя, кривая функции убывает медленнее.

Примерные графики функции MSSmall, показывающие влияние изменения значения Множителя стандартного отклонения.

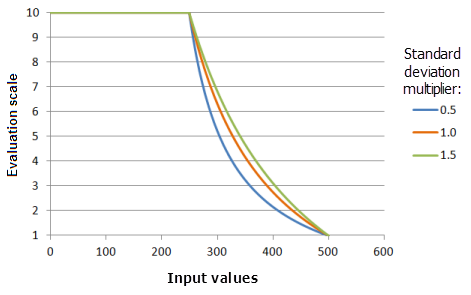
Функция, использованная для графика выше:

• TfMSSmall(1, StandardDeviationMultiplier, 0, 1, 500, 10)

  Где значения, использованные для стандартного отклонения, включают: 0,5, 1,0 и 1,5. Средний множитель (Mean multiplier), равный 1, и Множитель стандартного отклонения (Standard deviation multiplier), равный 1, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Функция Ближайший (Near)

Обзор

Функция преобразования Ближайший (Near) наиболее полезна, если наибольшее предпочтение отдаётся близким к указанному значению. Если середина расположена между нижним и верхним порогами, входное значение, равное середине, присваивается значению До масштаба (To scale). Остальные входные значения снижаются по оценочной шкале (снижение предпочтения), так как их значения удаляются от середины в обоих направлениях, пока они не достигнут значения От масштаба (From scale).

Функции преобразования Ближайший и Гауссова могут быть похожи, в зависимости от заданных параметров. Функция Ближайший (Near) обычно снижается более быстрыми темпами, с более узким разбросом, чем Гауссова функция. Поэтому она используется, когда более предпочтительны значения очень близкие к середине.

Случай применения

Как и в модели пригодности солнечных панелей, о которой шла речь в случае использования Гауссовой функции преобразования, исключение южных аспектов гораздо более предпочтительно.

Влияние параметров

Середина

Середина (Midpoint): также как и середина для Гауссовой функции, определяет центр кривой функции.

Примерные графики функции Ближайший (Near), показывающие влияние изменения значения Середины.

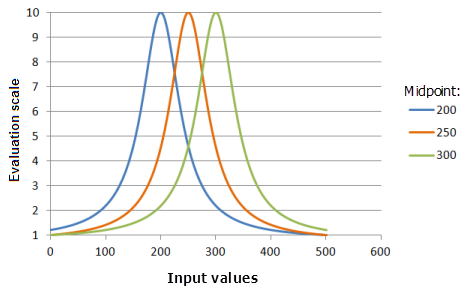
Функция, использованная для графика выше:

• TfNear(Midpoint, 0.000576, 0, 1, 500, 10)

  Где значения середины Midpoint - 200, 250 и 300. Середина (Midpoint), равная 250, и Разброс (Spread), равный 0,000576, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Разброс

Параметр Разброс (Spread) подобен Гауссовой функции, за исключением более драматического эффекта, достигаемого по мере удаления входных значений от середины

Примерные графики функции Ближайший (Near), показывающие влияние изменения значения Разброса.

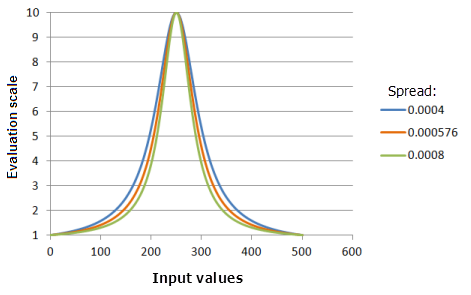
Функция, использованная для графика выше:

• TfNear(250, Spread, 0, 1, 500, 10)

  Где значения, использованные для Spread, включают: 0,0004, 0,000576 и 0,008. Середина (Midpoint), равная 250, и Разброс (Spread), равный 0,000576, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Функция Степень (Power)

Обзор

Функция преобразования Степень (Power) применяет степенную функцию ко входным данным поднятым на заданную экспоненту с использованием определенного сдвига. В модели пригодности, функцию Степень (Power) лучше использовать тогда, когда низкие входные значения являются наименее предпочтительными, но по мере увеличения входных значений предпочтения увеличиваются до достижения больших входных значений, где предпочтения увеличиваются быстро (это поведение зависит от экспоненты).

Случай применения

В модели пригодности для размещения атомной электростанции перемасштабировать расстояние от разломов для критерия безопасности. Местоположения удалённые от линии разлома постоянно увеличиваются в предпочтении на основе степенной функции, то есть места, расположенные дальше от линии разлома являются значительно более предпочтительными, чем места, находящиеся ближе к местоположению разлома.

Влияние параметров

Сдвиг

Параметр Сдвиг (Shift) является значением, вычитаемым из входных значений, которое может управлять начальным входным значением для степенных вычислений. Например, в случае с атомной электростанцией, было установлено, что она не должна быть построена ближе 10 километров от линии разлома. Вы можете сдвинуть функцию, так что функция Степень (Power) будет начинаться с 10 километров.

Примерные графики функции Степень (Power), показывающие влияние изменения значения Сдвига.

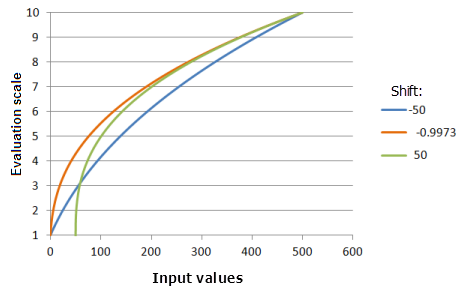
Функция, использованная для графика выше:

• TfPower(Shift, 0.3704, 0, 1, 500, 10)

  Где значения, использованные для Shift, включают: -50,0, -0,9973 и 50,0. Сдвиг (Shift), равный -0,9973, и Экспонента (Exponent), равная 0,3704, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Порядок

Параметр Экспонента (Exponent) контролирует, как круто возрастает функция Степень (Power). Чем больше экспонента, тем круче кривая функции, особенно при больших входных значениях.

Примерные графики функции Логистического роста (Logistic Growth), показывающие влияние изменения значения Экспоненты.

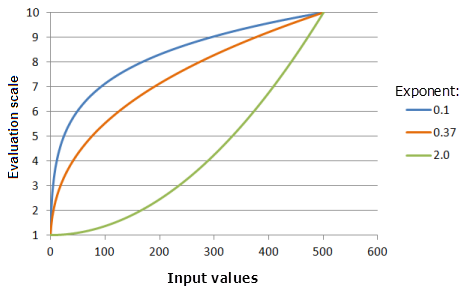
Входные параметры для графика выше:

• TfPower(-0.9973, Exponent, 0, 1, 500, 10)

  Где значения, использованные для Exponent, включают: 0,1, 0,37 и 2,0. Сдвиг (Shift), равный -0.9973, и Экспонента (Exponent), равная 0.3704, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Функция Small

Обзор

Функция преобразования Малый (Small) используется, если малые входные значения являются более предпочтительными. Заданная середина определяет точку перехода для функции. Значения выше середины, уменьшаются в предпочтении и значения ниже середины увеличиваются в предпочтении. Как быстро значения будут увеличиваться и уменьшаться по мере удаления от середины, определяется форморегулирующим параметром Разброс (Spread).

Случай применения

В модели пригодности жилья, вы можете перемасштабировать расстояние до набора данных дорог по стоимости для критерия постройки. Местоположения более близкие к дорогам (малые значения) имеют наибольшее предпочтение (ниже затраты), со значениями предпочтения постоянно уменьшающимися по мере увеличения расстояния от дорог.

Влияние параметров

Середина

Середина (Midpoint): определяет точку перехода функции. Сдвиг её в сторону больших, чем середина, значений во входных данных изменяет точку перехода, что приводит к увеличению в диапазоне меньших значений, которые являются более предпочтительными слева от середины, с предпочтением, увеличивающимся медленнее.

Примерные графики функции Малый (Small), показывающие влияние изменения значения Середины.

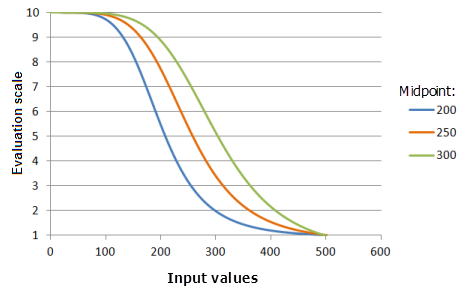
Функция, использованная для графика выше:

• TfSmall(Midpoint, 5, 0, 1, 500, 10)

  Где значения середины Midpoint – 200, 250 и 300. Середина (Midpoint), равная 250, и Разброс (Spread), равный 5, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Разброс

Разброс (Spread): контролирует, как быстро убывает и возрастает предпочтение. По мере увеличения разброса, входные значения, меньшие, чем середина, будут быстрее увеличиваться в предпочтении при приближении к нижнему порогу, и входные значения, большие, чем середина, будут быстрее снижаться в предпочтении при приближении к верхнему порогу.

Примерные графики функции Малый (Small), показывающие влияние изменения значения Разброса

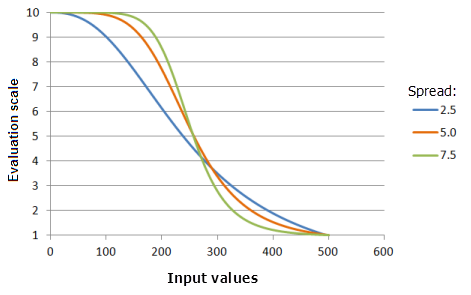
Функция, использованная для графика выше:

• TfSmall(250, Spread, 0, 1, 500, 10)

  Где значения середины Spread - 2,5, 5,0 и 7,5. Середина (Midpoint), равная 250, и Разброс (Spread), равный 5, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Симметричная линейная функция

Обзор

Функция преобразования Симметричная линейная (Symmetric Linear) применяет линейную функцию между указанными минимальным и максимальным значениями, которые зеркально отражаются вокруг середины между Минимумом (Minimum) и Максимумом (Maximum). Соответствующее входное значение для зеркально отображённой точки получает наибольшее значение предпочтения, с входными значениями линейно уменьшающимися в предпочтении, поскольку они удаляются от зеркально отображённой точки. Любые входные значения ниже Минимума (Minimum), но выше Нижнего порога (Lower threshold), или выше Максимума (Maximum), но ниже Верхнего порога (Upper threshold) будут присвоены значению От масштаба (From scale).

Если Минимум (Minimum) больше Максимума (Maximum), то устанавливается отрицательное линейное отношение (отрицательный уклон).

Симметричную линейную функцию лучше использовать, когда самое высокое предпочтение отдаётся значению середины, с предпочтениями увеличивающимися и уменьшающимися линейно по мере удаления входных значений от середины.

Случай применения

Переносящие конкретное заболевание насекомые наименее активны при температуре 70 градусов по Фаренгейту. Поскольку средняя температура повышается или понижается по направлению к минимуму и максимуму средних температур в пределах области исследования, насекомое является более активным, что приводит к большему числу случаев заболеваний людей. При выборе места для региональной базы отдыха, районы со средней температурой 70 градусов (средняя температура) являются наиболее предпочтительными, при этом предпочтение линейно снижается по мере увеличения и уменьшения температуры от 70 градусов, пока не будет достигнуты минимальная и максимальная средние температуры в пределах изучаемой территории.

Влияние параметров

Минимум (Minimum)

Параметр Минимум (Minimum) устанавливает одну из точек, через которую должна пройти функция SymmetricLinear. Изменение минимума может изменить середину, относительно которой функция отражается. Вы можете также изменить значение минимума от минимума входного растра для соответствия предпочтения явления критерию.

Примерные графики функции Симметричная линейная (Symmetric Linear), показывающие влияние изменения значения Минимума.

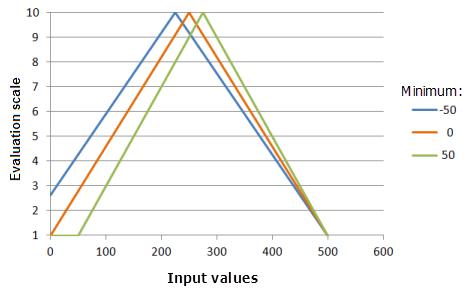
Функция, использованная для графика выше:

• TfSymmetricLinear(Minimum, 500, 0, 1, 500, 10)

  Где значения минимума Minimum – -50, 0 и 50. Минимум (Minimum), равный 0, и Максимум (Maximum), равный 500, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.

Максимум (Maximum)

Максимум (Maximum): устанавливает вторую точку, через которую должна пройти функция SymmetricLinear. Изменение максимума может изменить середину, относительно которой функция отражается. Вы можете также изменить значение максимума от максимума входного растра для соответствия предпочтения явления критерию.

Примерные графики функции Симметричная линейная (Symmetric Linear), показывающие влияние изменения значения Максимума.

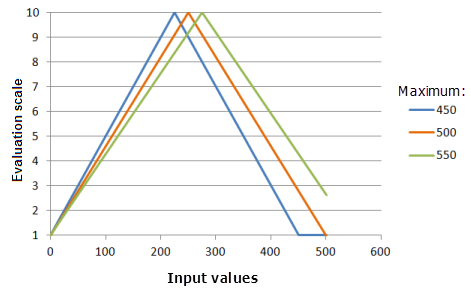
Функция, использованная для графика выше:

• TfSymmetricLinear(0, Maximum, 0, 1, 500, 10)

  Где значения, использованные для Maximum, включают: 450, 500 и 550. Минимум (Minimum), равный 0, и Максимум (Maximum), равный 500, являются значениями параметров, рассчитанными по умолчанию, для входного набора данных с диапазоном от 0 до 500.